\({\color{Red}{欢迎到学科网下载资料学习 }}\)
[ 【基础过关系列】高二数学同步精品讲义与分层练习(人教A版2019）]
( https://www.zxxk.com/docpack/2875423.html)
\({\color{Red}{ 跟贵哥学数学，so \quad easy！}}\)
选择性第二册同步巩固，难度2颗星！
基础知识
函数单调性与导数
在某个区间\((a ,b)\)内，若\(f'(x)>0\)，则函数\(y=f(x)\)在这个区间内单调递增；
若\(f'(x)<0\) ，则函数\(y=f(x)\)在这个区间内单调递减．
解释
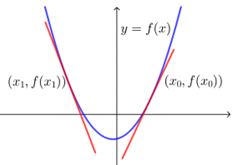
(1) 如下图，导数\(f' (x_0)\)表示函数\(y=f(x)\)的图象在点\((x_0，f(x_0))\)处的切线的斜率，可发现，
在\(x=x_0\)处，\(f' (x_0 )>0\)，切线是“左下右上”的上升式，函数\(f(x)\)的图象也是上升的，函数\(f(x)\))在\(x=x_0\)附近单调递增；
在\(x=x_1\)处，\(f' (x_1 )<0\)，切线是“左上右下”的下降式，函数\(f(x)\)的图象也是下降的，函数\(f(x)\)在\(x=x_1\)附近单调递减.
(2) 若函数\(y=f(x)\)在某个区间\((a ,b)\)内单调递增，则\(∀x∈(a ,b)\) ,\(f' (x)≥0\)(含等号)恒成立，但不存在一区间\((c ,d)⊆(a ,b)\)内使得\(f' (x)=0\)；
假如存在一区间\((c ,d)⊆(a ,b)\)内使得\(f' (x)=0\)，那原函数\(y=f(x)\)在区间\((c ,d)\)内恒等于一个常数，即\(f(x)=m\)(\(m\)是个常数)，则原函数不可能在\((a ,b)\)内单调递增.
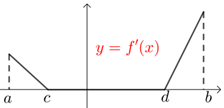\(\qquad \qquad\)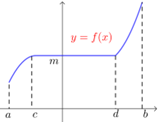 
函数\(y=f(x)\)在某个区间\((a ,b)\)内单调递减有类似结论！
(3)导函数“穿线图”与原函数“趋势图”
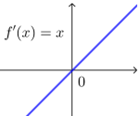
① 导函数“穿线图”关注导函数在各区间的正负，故特别注意函数与x轴的交点情况，
如\(f'(x)=x\)与\(f' (x)=e^x-1\)的“穿线图”视为一样的，它们在\((-∞,0)\)上为负，在\((0,+∞)\)上为正.
\(\qquad \qquad\)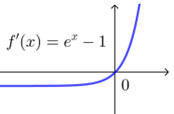 
② 原函数“趋势图”仅关注函数在各区间上的单调性，没顾及其最值或曲线形状等，
如由导函数\(f' (x)=x-1\)的“穿线图”易得原函数\(y=f(x)\)在\((-∞,0)\)上递减，在\((0,+∞)\)上为递增，趋势图可如下图，
③ 后面涉及到函数单调性均可通过分析导函数“穿线图”得出原函数的单调性.
对含参函数单调性的分析思路
(1) 如何分析原函数的单调性？
答：分析原函数的单调性等价于分析导函数的正负性.
(2) 那如何分析导函数的正负性呢？.
答：数形结合，若能得到导函数的“穿线图”(即解导数不等式，与其零点有莫大关系))，看图“说话”便可，进而得出原函数的“趋势图”(即原函数的大致趋势)也不难了(看下图).
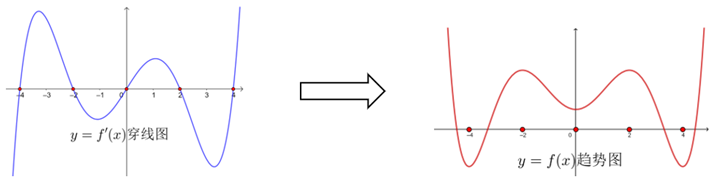
(导函数看“零点”，原函数看单调性)
(3) 那要得到导函数的“穿线图”，要注意什么呢？
答：掌握“一次函数”型、“二次函数”型、“指数函数”型常见模型，画“穿线图”思考以下问题：
① 导函数是否存在零点；
② 若存在，有几个零点呢？若有两个以上，哪个零点大？
③ 零点是否在定义域内？
(4) 怎么做到准确的分类讨论呢？
答：① 熟悉模型，确定分类讨论的标准；
② 做到分类讨论“不漏不重”，把每项分类看成一个集合，每个集合的交集为空集则“不重”，所有集合的并集为参数的全集则为“不漏”.
各模型分类讨论的标准
分类讨论要确定每步分类的标准，做到有根有据.
“一次函数”型：是否一次函数，直线斜率大于0还是小于0，函数零点与定义域端点的大小；
“二次函数”型：确定是否二次函数，开口方向，判别式(是否有零点)，零点比较大小，零点与定义域端点的大小；
“指数函数”型：是否存在零点；利用导函数正负性的等价可转化为二次函数讨论.
【例】 利用导数的方法求函数\(f(x)= \dfrac{a}{2} x^2-x\)的单调性.
解 \(f'(x)=ax-1\)，
① 当\(a=0\)时，\(f'(x)=-1<0\)，\(f(x)\)在\(R\)上递减；
② 当\(a>0\)时，令\(f'(x)=ax-1>0\)，解得\(x> \dfrac{1}{a}\)；令\(f'(x)=ax-1<0\)，解得\(x< \dfrac{1}{a}\)；
所以\(f(x)\)在\(\left(-\infty, \dfrac{1}{a}\right)\)上递减；在\(\left(\dfrac{1}{a},+\infty\right)\)上递增；
③ 当\(a<0\)时，令\(f'(x)=ax-1>0\)，解得\(x< \dfrac{1}{a}\)；令\(f'(x)=ax-1<0\)，解得\(x> \dfrac{1}{a}\)；
所以\(f(x)\)在\(\left(\dfrac{1}{a},+\infty\right)\)上递减；在\(\left(-\infty, \dfrac{1}{a}\right)\)上递增.
解不等式\(ax-1>0\)时，不能想当然:\(x> \dfrac{1}{a}\)；要分\(a=0\)，\(a>0\)，\(a<0\)三种情况讨论.
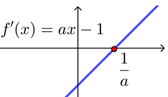
也可以借助导函数“穿线图”的想法(研究导函数的在各区间的正负)，得到相同结果.
| \(a=0\)时 | \(a>0\)时 | \(a<0\)时 | |
|---|---|---|---|
| 导函数“穿线图” |  |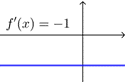
 |
 |
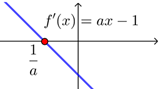| 原函数单调性 | 在\(R\)上递减 | 在\(\left(-\infty, \dfrac{1}{a}\right)\)上递减 \(\left(\dfrac{1}{a},+\infty\right)\)上递增 |
在\(\left(\dfrac{1}{a},+\infty\right)\)上递减 在\(\left(-\infty, \dfrac{1}{a}\right)\)上递增 |
基本方法
情况1 一次函数型
【典题1】 求函数\(f(x)=xe^{kx}\)的单调区间.
解析 \(f^{\prime}(x)=e^{k x}+k x e^{k x}=e^{k x}(k x+1)\)
令\(f'(x)=0\)，即\(kx+1=0\) (对\(y=kx+1\)的函数类型讨论)
(1)若\(k=0\)时，\(f'(x)=1>0\)，\(f(x)\)在\(R\)上为增函数，
(2)若\(k≠0\)时，则由\(kx+1=0\)得\(x=- \dfrac{1}{k}\) (需要对\(y=kx+1\)的斜率正负讨论)
① 若\(k>0\)时，
当\(x<- \dfrac{1}{k}\)时，\(f'(x)<0\)，\(f(x)\)递减；当\(x>- \dfrac{1}{k}\)时，\(f'(x)>0\)，\(f(x)\)递增；
② 当\(k<0\)时，
当\(x<- \dfrac{1}{k}\)时，\(f'(x)>0\)，\(f(x)\)递增；当\(x<- \dfrac{1}{k}\)时，\(f'(x)<0\)，\(f(x)\)递减；
综上所述：
若\(k=0\)，\(f(x)\)在\(R\)上为增函数；
若\(k>0\)，则\(f(x)\)在\(\left(-\infty,-\dfrac{1}{k}\right)\)上为减函数，在\(\left(-\dfrac{1}{k},+\infty\right)\)上为增函数；
若\(k<0\)，则\(f(x)\)在\(\left(-\infty,-\dfrac{1}{k}\right)\)上为增函数，在\(\left(-\dfrac{1}{k},+\infty\right)\)上为减函数.
点拨 对导函数是一次函数型\(f'(x)=kx+b\)，要分\(k=0\)，\(k>0\)，\(k<0\)三种情况讨论.
【巩固练习】
1.求函数\(f(x)=mxe^x-e^x\)(\(m∈R\)，\(e\)是自然对数的底数)的单调性.
参考答案
- 答案 若\(m=0\)时，\(f(x)\)在\(R\)上单调递减；
若\(m>0\)时，\(f(x)\)在\(\left(\dfrac{1}{m}-1,+\infty\right)\)上单调递增，在\(\left(-\infty, \dfrac{1}{m}-1\right)\)上单调递减；
若\(m<0\)时，\(f(x)\)在\(\left(\dfrac{1}{m}-1,+\infty\right)\)单调递减，在\(\left(-\infty, \dfrac{1}{m}-1\right)\)单调递增.
解析 \(f'(x)=m(e^x+xe^x )-e^x=(mx+m-1)e^x\)，
(1)若\(m=0\)时，则\(f'(x)=-e^x<0\)，则\(f(x)\)在\(R\)上单调递减，
(2)若\(m>0\)时，当\(x \in\left(\dfrac{1}{m}-1,+\infty\right)\)时，\(f'(x)>0\)，函数单调递增，
\(x \in\left(-\infty, \dfrac{1}{m}-1\right)\)时，\(f'(x)<0\)，函数单调递减；
(3)若\(m<0\)时，当\(x \in\left(\dfrac{1}{m}-1,+\infty\right)\)时，\(f'(x)<0\)，函数单调递减，
\(x \in\left(-\infty, \dfrac{1}{m}-1\right)\)时，\(f'(x)>0\)，函数单调递增.
情况2 二次函数型
【典题1】 求函数\(f(x)=\dfrac{x^3}{3}-\dfrac{a+2}{2} x^2+2 a x+1\)的单调性.
解析 \(f'(x)=x^2-(a+2)x+2a=(x-2)(x-a)\)，
(求导后因式分解，确定导函数是否存在零点，若有，是多少，有几个？)
(1)若\(a=2\)时，\(f(x)\)在\(R\)上递增；
(2)若\(a>2\)时，
当\(2<x<a\)时，\(f'(x)<0\)，\(f(x)\)递减；
当\(x>a\)或\(x<2\)时，\(f'(x)>0\)，\(f(x)\)递增；
(3)若\(a<2\)时，
当\(a<x<2\)时，\(f'(x)<0\)，\(f(x)\)递减；
当\(x>2\)或\(x<a\)时，\(f'(x)>0\)，\(f(x)\)递增.
点拨 导函数\(f'(x)=(x-a)(x-b)\)有零点，要分\(a=b\)，\(a>0\)，\(a<b\)三种情况讨论，
再结合导函数的穿线图进行分析.
【典题2】 若函数\(f(x)=a x+\dfrac{2}{x}+\ln x(a \geq 0)\)，求函数\(f(x)\)的单调区间.
解析 \(f^{\prime}(x)=a-\dfrac{2}{x^2}+\dfrac{1}{x}=\dfrac{a x^2+x-2}{x^2}(x>0)\)，
令\(g(x)=ax^2+x-2\)(这不一定是二次函数，需要讨论函数类型)
① 若\(a=0\)，\(g(x)=x-2\)，
当\(0<x<2\)时，\(g(x)<0\)，\(f'(x)<0\)；当\(x>2\)时，\(g(x)>0\)，\(f'(x)>0\)；
\(\therefore f(x)\)在\((0,2)\)上为减函数，在\((2,+∞)\)上为增函数
② 若\(a>0\)，则\(∆=1+8a>0\)，
由\(ax^2+x-2=0\)得\(x_1=\dfrac{-1-\sqrt{1+8 a}}{2 a}<0\)， \(x_2=\dfrac{-1+\sqrt{1+8 a}}{2 a}>0\)，
(作出 \(g(x)=ax^2+x-2\)的图像，由图像可知)
\(f(x)\)在\((0,x_2)\)上为减函数，在\((x_2,+∞)\)上为增函数.
综上所述：
\(a=0\)时，\(f(x)\)在\((0,2)\)上为减函数，在\((2,+∞)\)上为增函数
\(a>0\)时，\(f(x)\)在\(\left(0, \dfrac{-1+\sqrt{1+8 a}}{2 a}\right)\)上为减函数，在\(\left(\dfrac{-1+\sqrt{1+8 a}}{2 a},+\infty\right)\)上为增函数.
点拨 对于导函数\(f'(x)=ax^2+bx+c\)中二次项系数\(a\)不确定，要分\(a=0\)，\(a>0\)，\(a<0\)三种情况讨论；导函数\(f'(x)=ax^2+bx+c\)中若不能因式分解，由于不确定是否存在零点，要分\(∆=0\)，\(∆>0\)，\(∆<0\)三种情况讨论.
【巩固练习】
1.求函数\(f(x)= \dfrac{1}{3} x^3+ \dfrac{a}{2} x^2-2ax+1\)的单调性.
2.已知函数\(f(x)=p\ln x+(p-1) x^2+1\)， 当\(p>0\)时，讨论函数\(f(x)\)的单调性.
参考答案
-
答案 当\(-2<a<0\)时， \(f(x)\)在\(R\)上递增；
当\(a<-2\)或\(a>0\)时，\(f(x)\)在\(\left(\dfrac{-a-\sqrt{4 a^2+8 a}}{2}, \dfrac{-a+\sqrt{4 a^2+8 a}}{2}\right)\)上递减，
在 \(\left(-\infty, \dfrac{-a-\sqrt{4 a^2+8 a}}{2}\right)\), \(\left(\dfrac{-a+\sqrt{4 a^2+8 a}}{2},+\infty\right)\)递增.
解析 \(f'(x)=x^2+ax-2a\)，其判别式为\(∆=4a^2+8a\)，
若\(∆≤0\)，即\(-2<a<0\)时，\(f'(x)>0\)，\(f(x)\)在\(R\)上递增；
若\(∆≤0\)，即\(a<-2\)或\(a>0\)时，
令\(f'(x)=0\)，解得\(x_1=\dfrac{-a-\sqrt{4 a^2+8 a}}{2}\)或\(x_2=\dfrac{-a+\sqrt{4 a^2+8 a}}{2}\)，其中\(x_2>x_1\)，
当\(x_1<x<x_2\)时，\(f'(x)<0\)， \(f(x)\)递减；
当\(x>x_2\)或\(x<x_1\)时，\(f'(x)>0\)，\(f(x)\)递增.
综上所述，当\(-2<a<0\)时， \(f(x)\)在\(R\)上递增；
当\(a<-2\)或\(a>0\)时，\(f(x)\)在\(\left(\dfrac{-a-\sqrt{4 a^2+8 a}}{2}, \dfrac{-a+\sqrt{4 a^2+8 a}}{2}\right)\)上递减，
在 \(\left(-\infty, \dfrac{-a-\sqrt{4 a^2+8 a}}{2}\right)\), \(\left(\dfrac{-a+\sqrt{4 a^2+8 a}}{2},+\infty\right)\)递增. -
答案 当\(p≥1\)时，\(f(x)\)在\((0,+∞)\)单调递增；
当\(0<p<1\)时，\(f(x)\)在\(\left(0, \sqrt{\dfrac{p}{2(1-p)}}\right)\)单调递增，在\(\left(\sqrt{\dfrac{p}{2(1-p)}},+\infty\right)\)单调递减.
解析 \(f(x)\)的定义域为\((0,+∞)\)，
\(f^{\prime}(x)=\dfrac{p}{x}+2(p-1) x=\dfrac{2(p-1) x^2+p}{x}\)，
(1)若\(p=1\)时，\(f'(x)= \dfrac{1}{x}>0\)，故\(f(x)\)在\((0,+∞)\)单调递增；
(2)若\(p≠1\)时，
①若\(p>1\)时，\(f'(x)>0\)，故\(f(x)\)在\((0,+∞)\)单调递增；
②若\(0<p<1\)时，令\(f'(x)=0\)，解得\(x=\sqrt{\dfrac{p}{2(1-p)}}\)，
则当\(x \in\left(0, \sqrt{\dfrac{p}{2(1-p)}}\right)\)时，\(f'(x)>0\)； \(x \in\left(\sqrt{\dfrac{p}{2(1-p)}},+\infty\right)\)时，\(f'(x)<0\).
故\(f(x)\)在\(\left(0, \sqrt{\dfrac{p}{2(1-p)}}\right)\)单调递增，在\(\left(\sqrt{\dfrac{p}{2(1-p)}},+\infty\right)\)单调递减.
综上所述
当\(p≥1\)时，\(f(x)\)在\((0,+∞)\)单调递增；
当\(0<p<1\)时，\(f(x)\)在\(\left(0, \sqrt{\dfrac{p}{2(1-p)}}\right)\)单调递增，在\(\left(\sqrt{\dfrac{p}{2(1-p)}},+\infty\right)\)单调递减.
情况3 指数函数型
【典题1】 已知函数\(f(x)=e^x+ax\)求函数的单调区间.
解析 \(f'(x)=e^x+a\)，
(1)若\(a≥0\)时，\(f'(x)>0\)，\(f(x)\)在\(R\)上递增；
(2)若\(a<0\)时，令\(f(x)=0\),解得\(x=\ln (-a)\),
(此时\(f'(x)=e^x+a\)与\(y=x-\ln (-a)\)的符号是一致的)
当\(x>\ln (-a)\)时，\(f'(x)>0\)，\(f(x)\)递增；
当\(x<\ln (-a)\)时，\(f'(x)<0\)， \(f(x)\)递减.
综上所述：
若\(a≥0\)时，\(f(x)\)在\(R\)上递增；
若\(a<0\)时，\(f(x)\)在\((\ln (-a),+∞)\)递增，\(f(x)\)在\((-∞,\ln (-a))\)递减.
【巩固练习】
1.讨论\(f(x)=e^{x+a}+ax\)的单调性.
2.求函数\(f(x)= \dfrac{a}{2} x^2+xe^x+ax(a∈R)\)的单调性.
参考答案
-
答案 当\(a≥0\)时，\(f(x)\)在\((-∞,+∞)\)上单调递增；
当\(a<0\)时，\(f(x)\)在\((-∞,-a+\ln (-a))\)上单调递减，
在\((-a+\ln (-a),+∞)\)上单调递增．
解析 \(f'(x)=e^{x+a}+a\)，\(x∈R\)．\(f'(x)\)在\(R\)上单调递增．
当\(a≥0\)时，\(f'(x)>0\)，\(f(x)\)在\((-∞,+∞)\)上单调递增；
当\(a<0\)时，\(f'(x)=0⇔x=-a+\ln (-a)\)，
\(f'(x)<0⇔x<-a+\ln (-a)\)，
\(f'(x)>0⇔x>-a+\ln (-a)\)，
\(\therefore f(x)\)在\((-∞,-a+\ln (-a))\)上单调递减，在\((-a+\ln (-a),+∞)\)上单调递增．
综上所述：
当\(a≥0\)时，\(f(x)\)在\((-∞,+∞)\)上单调递增；
当\(a<0\)时，\(f(x)\)在\((-∞,-a+\ln (-a))\)上单调递减，在\((-a+\ln (-a),+∞)\)上单调递增． -
答案 当\(a≥0\)时，\(f(x)\)在\((-∞,-1)\)递减，在\((-1,+∞)\)递增，
当\(-\dfrac{1}{e}<a<0\)时，\(f(x)\)在\((\ln (-a),-1)\)递减，在\((-∞,\ln (-a))\),\((-1,+∞)\)递增，
当\(a=-\dfrac{1}{e}\)时，\(f(x)\)在\(R\)递增，
当\(a<-\dfrac{1}{e}\)时，\(f(x)\)在\((-1,\ln (-a))\)递减，在\((-∞,-1)\),\((\ln (-a),+∞)\)递增.
解析 \(f'(x)=ax+e^x+xe^x+a=e^x (x+1)+a(x+1)=(x+1)(e^x+a)\)，
(1)若\(a≥0\)时，\(e^x+a>0\)
当\(x<-1\)时，\(f'(x)<0\)；当\(x>-1\)时，\(f'(x)>0\)；
(2)若\(a<0\)时，由\(f'(x)=0\)，解得\(x_1=-1\)或\(x_2=\ln (-a)\)，
①若\(a=-\dfrac{1}{e}\)时，则\(\ln (-a)=-1⇒x_1=x_2\)，\(f'(x)≥0\)恒成立，
故\(f(x)\)在\(R\)递增；
②若\(-\dfrac{1}{e}<a<0\)，则\(\ln (-a)<-1⇒x_1<x_2\)，
当\(\ln (-a)<x<-1\)时，\(f'(x)<0\)，\(f(x)\)递减；
当\(x<\ln (-a)\)或\(x>-1\)时，\(f'(x)>0\)，\(f(x)\)递增.
③若\(a<-\dfrac{1}{e}\)，则\(\ln (-a)>-1⇒x_1>x_2\)，
当\(-1<x<\ln (-a)\)时，\(f'(x)<0\)，\(f(x)\)递减；
当\(x<-1\)或\(x>\ln (-a)\)时，\(f'(x)>0\)，\(f(x)\)递增.
综上，
当\(a≥0\)时，\(f(x)\)在\((-∞,-1)\)递减，在\((-1,+∞)\)递增，
当\(-\dfrac{1}{e}<a<0\)时，\(f(x)\)在\((\ln (-a),-1)\)递减，在\((-∞,\ln (-a))\),\((-1,+∞)\)递增，
当\(a=-\dfrac{1}{e}\)时，\(f(x)\)在\(R\)递增，
当\(a<-\dfrac{1}{e}\)时，\(f(x)\)在\((-1,\ln (-a))\)递减，在\((-∞,-1)\),\((\ln (-a),+∞)\)递增.
分层练习
【A组---基础题】
1.求函数\(f(x)=a\ln x-ax-3\)的单调区间.
2.讨论函数\(f(x)=x^3+ax^2+x+1\)的单调区间.
3.求函数\(f(x)=ax^2+(2-a)\ln x+2\)的单调性.
4.讨论函数\(f(x)=(a+1)\ln x+ax^2+1\)的单调性.
5.求函数\(f(x)=- \dfrac{1}{2} a(x-1)^2+(x-2) e^x (a>0)\)的单调性.
6.求函数\(f(x)=\ln x-(a+2)x+ax^2 (a∈R)\)的单调区间.
7.求函数\(f(x)= \dfrac{a}{2} x^2+xe^x+ax(a∈R)\)的单调性.
参考答案
-
答案 若\(a=0\)，函数不具有单调性；
若\(a>0\)，函数\(f(x)\)在\((0,1)\)上单调递增，在\([1,+∞)\)上单调递减；
若\(a<0\)，函数\(f(x)\)在\((0,1)\)上单调递减，在\([1,+∞)\)上单调递增.
解析 易知，函数的定义域为\((0,+∞)\)，
因为\(f^{\prime}(x)=\dfrac{a}{x}-a=\dfrac{a(1-x)}{x}\)．
若\(a=0\)，则\(f'(x)=0\)，此时原函数不具有单调性；
若\(a>0\)，当\(x∈(0,1)\)时，\(f'(x)>0\)，此时函数\(f(x)\)为增函数，
当\(x∈[1,+∞)\)时，\(f'(x)<0\)，此时函数\(f(x)\)为减函数；
若\(a<0\)，当\(x∈(0,1)\)时，\(f'(x)<0\)，此时函数\(f(x)\)为减函数，
当\(x∈[1,+∞)\)时，\(f'(x)>0\)，此时函数\(f(x)\)为增函数.
综上所述：
若\(a=0\)，函数不具有单调性；
若\(a>0\)，函数\(f(x)\)在\((0,1)\)上单调递增，在\([1,+∞)\)上单调递减；
若\(a<0\)，函数\(f(x)\)在\((0,1)\)上单调递减，在\([1,+∞)\)上单调递增. -
答案 当 \(-\sqrt{3}≤a≤\sqrt{3}\)时，\(f(x)\)在\(R\)上为增函数，
当\(a<-\sqrt{3}\)或\(a>\sqrt{3}\)时，\(f(x)\)在 \(\left(-\infty, \dfrac{-a-\sqrt{a^2-3}}{3}\right)\), \(\left(\dfrac{-a+\sqrt{a^2-3}}{3},+\infty\right)\)上为增函数，在 \(\left(\dfrac{-a-\sqrt{a^2-3}}{3}, \dfrac{-a+\sqrt{a^2-3}}{3}\right)\)上为减函数.
解析 \(f'(x)=3x^2+2ax+1\)，\(∆=4a^2-12\)， (注意这里根的存在需要讨论)
①若\(∆=4a^2-12≤0\)，即\(-\sqrt{3}≤a≤\sqrt{3}\)，
则\(f(x)\)在\(R\)上为增函数；
②若\(∆=4a^2-12>0\)，即\(a<-\sqrt{3}\) 或\(a>\sqrt{3}\)，
由\(f'(x)=0\)得\(\chi_1=\dfrac{-a-\sqrt{a^2-3}}{3}\)， \(x_2=\dfrac{-a+\sqrt{a^2-3}}{3}\)，
\(f(x)\)在 \(\left(-\infty, \dfrac{-a-\sqrt{a^2-3}}{3}\right)\)或 \(\left(\dfrac{-a+\sqrt{a^2-3}}{3},+\infty\right)\)上为增函数，
在 \(\left(\dfrac{-a-\sqrt{a^2-3}}{3}, \dfrac{-a+\sqrt{a^2-3}}{3}\right)\)上为减函数.
综上所述：
当 \(-\sqrt{3}≤a≤\sqrt{3}\)时，\(f(x)\)在\(R\)上为增函数，
当\(a<-\sqrt{3}\)或\(a>\sqrt{3}\)时，\(f(x)\)在 \(\left(-\infty, \dfrac{-a-\sqrt{a^2-3}}{3}\right)\), \(\left(\dfrac{-a+\sqrt{a^2-3}}{3},+\infty\right)\)上为增函数，在 \(\left(\dfrac{-a-\sqrt{a^2-3}}{3}, \dfrac{-a+\sqrt{a^2-3}}{3}\right)\)上为减函数. -
答案 \(a<0\)时，函数\(f(x)\)在 \(\left(0, \sqrt{\dfrac{a-2}{2 a}}\right)\)上单调递增，在\(\left(\sqrt{\dfrac{a-2}{2 a}},+\infty\right)\)单调递减．
\(0≤a≤2\)时，函数在\((0,+∞)\)上单调递增，
\(a>2\)时，函数\(f(x)\)在 \(\left(0, \sqrt{\dfrac{a-2}{2 a}}\right)\)上单调递减，在\(\left(\sqrt{\dfrac{a-2}{2 a}},+\infty\right)\)单调递增．
解析 依题意，函数\(f(x)\)的定义域为\((0,+∞)\)，
\(f^{\prime}(x)=2 a x+\dfrac{2-a}{x}=\dfrac{2 a x^2+2-a}{x}\)，
①\(a<0\)时，令\(2ax^2+2-a=0\)，可得\(x^2=\dfrac{a-2}{2 a}>0\)，
\(x=\sqrt{\dfrac{a-2}{2 a}}\)，(负值舍去)，
当\(x \in\left(0, \sqrt{\dfrac{a-2}{2 a}}\right)\)时，\(f'(x)>0\)，当\(x \in\left(\sqrt{\dfrac{a-2}{2 a}},+\infty\right)\)时，\(f'(x)<0\)，
故函数\(f(x)\)在 \(\left(0, \sqrt{\dfrac{a-2}{2 a}}\right)\)上单调递增，在 \(\left(\sqrt{\dfrac{a-2}{2 a}},+\infty\right)\)单调递减．
②\(0≤a≤2\)时，\(f'(x)>0\)恒成立，函数在\((0,+∞)\)上单调递增，
③\(a>2\)时，当\(x \in\left(0, \sqrt{\dfrac{a-2}{2 a}}\right)\)时，\(f'(x)<0\)，当\(x \in\left(\sqrt{\dfrac{a-2}{2 a}},+\infty\right)\)时，\(f'(x)>0\)，
故函数\(f(x)\)在 \(\left(0, \sqrt{\dfrac{a-2}{2 a}}\right)\)上单调递减，在\(\left(\sqrt{\dfrac{a-2}{2 a}},+\infty\right)\)单调递增．
综上， \(a<0\)时，函数\(f(x)\)在 \(\left(0, \sqrt{\dfrac{a-2}{2 a}}\right)\)上单调递增，在\(\left(\sqrt{\dfrac{a-2}{2 a}},+\infty\right)\)单调递减．
\(0≤a≤2\)时，函数在\((0,+∞)\)上单调递增，
\(a>2\)时，函数\(f(x)\)在 \(\left(0, \sqrt{\dfrac{a-2}{2 a}}\right)\)上单调递减，在\(\left(\sqrt{\dfrac{a-2}{2 a}},+\infty\right)\)单调递增． -
答案 当\(a≥0\)时，\(f(x)\)在\((0,+∞)\)上递增；
当\(a≤-1\)时，\(f(x)\)在\((0,+∞)\)上递减；
当\(-1<a<0\)时，\(f(x)\)在\(\left(0, \sqrt{-\dfrac{a+1}{2 a}}\right)\)上单调递增，在\(\left(\sqrt{-\dfrac{a+1}{2 a}},+\infty\right)\)上单调递减．
解析 \(f(x)\)的定义域为\((0,+∞)\)， \(f^{\prime}(x)=\dfrac{a+1}{x}+2 a x=\dfrac{2 a x^2+a+1}{x}\).
(1)当\(a=0\)时，\(f'(x)= \dfrac{1}{x}>0\)，\(f(x)\)在\((0,+∞)\)上递增；
(2)当 时，
①若\(a>0\)，\(f'(x)>0\)，\(f(x)\)在\((0,+∞)\)上递增；
②若\(a<0\)
ⅰ若\(a≤-1\)，\(f'(x)<0\)，\(f(x)\)在\((0,+∞)\)上递减；
ⅱ若\(-1<a<0\)，令\(f'(x)=0\)，解得\(x=\sqrt{-\dfrac{a+1}{2 a}}\)，
则当\(x \in\left(0, \sqrt{-\dfrac{a+1}{2 a}}\right)\)时，\(f'(x)>0\)；当 \(x \in\left(\sqrt{-\dfrac{a+1}{2 a}},+\infty\right)\)时，\(f'(x)<0\)；
故\(f(x)\)在\(\left(0, \sqrt{-\dfrac{a+1}{2 a}}\right)\)上单调递增，在\(\left(\sqrt{-\dfrac{a+1}{2 a}},+\infty\right)\)上单调递减．
综上所述；
当\(a≥0\)时，\(f(x)\)在\((0,+∞)\)上递增；
当\(a≤-1\)时，\(f(x)\)在\((0,+∞)\)上递减；
当\(-1<a<0\)时，\(f(x)\)在\(\left(0, \sqrt{-\dfrac{a+1}{2 a}}\right)\)上单调递增，在\(\left(\sqrt{-\dfrac{a+1}{2 a}},+\infty\right)\)上单调递减． -
答案 当\(0<a<e\)时，\(f(x)\)在\((1,+∞)\),\((-∞,\ln a)\)上单调递增，在\((\ln a,1)\)上单调递减；
当\(a=e\)时，\(f(x)\)在\(R\)上单调递增；
当\(a>e\)时，\(f(x)\)在\((\ln a,+∞)\),\((-∞,1)\)上单调递增，在\((1,\ln a)\)上单调递减.
解析 (1) \(f'(x)=-a(x-1)+(x-1)e^x=(x-1)(e^x-a)\)，
\(∵a>0\)，由\(f'(x)=0\)可得\(x=1\)或\(x=\ln a\)，
(i)当\(0<a<e\)时，\(1>\ln a\)，
在\((1,+∞)\),\((-∞,\ln a)\)上，\(f'(x)>0\)，\(f(x)\)单调递增，
在\((\ln a,1)\)上，\(f'(x)<0\)，\(f(x)\)单调递减；
(ii)当\(a=e\)时，\(\ln e=1\)，\(f'(x)>0\)在\(R\)上恒成立，即\(f(x)\)在\(R\)上单调递增；
(iii)当\(a>e\)时，\(\ln a>1\)，
在\((\ln a,+∞)\),\((-∞,1)\)上，\(f'(x)>0\)，\(f(x)\)单调递增，
在\((1,\ln a)\)上，\(f'(x)<0\)，\(f(x)\)单调递减；
综上所述，当\(0<a<e\)时，\(f(x)\)在\((1,+∞)\),\((-∞,\ln a)\)上单调递增，在\((\ln a,1)\)上单调递减；
当\(a=e\)时，\(f(x)\)在\(R\)上单调递增；
当\(a>e\)时，\(f(x)\)在\((\ln a,+∞)\),\((-∞,1)\)上单调递增，在\((1,\ln a)\)上单调递减. -
答案 当\(a≤0\)时，\(f(x)\)在\(\left(0, \dfrac{1}{2}\right)\)内单调递增，在 \(\left(\dfrac{1}{2},+\infty\right)\)内单调递减；
当\(0<a<2\)时，\(f(x)\)在\(\left(0, \dfrac{1}{2}\right)\)，\(\left(\dfrac{1}{a},+\infty\right)\)内单调递增，在\(\left(\dfrac{1}{2}, \dfrac{1}{a}\right)\)内单调递减；
当\(a=2\)时，所以\(f(x)\)在\((0,+∞)\)上单调递增；
当\(a>2\)时，\(f(x)\)在 \(\left(0, \dfrac{1}{a}\right)\)， \(\left(\dfrac{1}{2},+\infty\right)\)内单调递增，在\(\left(\dfrac{1}{a}, \dfrac{1}{2}\right)\)内单调递减．
解析 因为\(f(x)=\ln x-(a+2)x+ax^2\)，定义域为\((0,+∞)\)，
所以\(f^{\prime}(x)=\dfrac{1}{x}-(a+2)+2 a x=\dfrac{2 a x^2-(a+2) x+1}{x}=\dfrac{(2 x-1)(a x-1)}{x}\)．
①当\(a≤0\)时，\(f(x)\)与\(f'(x)\)在\((0,+∞)\)上的变化情况如下：
| \(x\) | \(\left(0, \dfrac{1}{2}\right)\) | \(\dfrac{1}{2}\) | \(\left(\dfrac{1}{2},+\infty\right)\) |
|---|---|---|---|
| \(f'(x)\) | \(+\) | \(0\) | \(-\) |
| \(f(x)\) | \(↗\) | \(↘\) |
所以\(f(x)\)在\(\left(0, \dfrac{1}{2}\right)\)内单调递增，在 \(\left(\dfrac{1}{2},+\infty\right)\)内单调递减．
②当\(0<a<2\)时，\(f(x)\)与\(f'(x)\)在\((0,+∞)\)上的变化情况如下：
| \(x\) | \(\left(0, \dfrac{1}{2}\right)\) | \(\dfrac{1}{2}\) | \(\left(\dfrac{1}{2}, \dfrac{1}{a}\right)\) | \(\dfrac{1}{a}\) | \(\left(\dfrac{1}{a},+\infty\right)\) |
|---|---|---|---|---|---|
| \(f'(x)\) | \(+\) | \(0\) | \(-\) | \(0\) | \(+\) |
| \(f(x)\) | \(↗\) | \(↘\) | \(↗\) |
所以\(f(x)\)在\(\left(0, \dfrac{1}{2}\right)\)，\(\left(\dfrac{1}{a},+\infty\right)\)内单调递增，在\(\left(\dfrac{1}{2}, \dfrac{1}{a}\right)\)内单调递减．
③当\(a=2\)时，\(f'(x)≥0\)，所以\(f(x)\)在\((0,+∞)\)上单调递增．
④当a>2时，\(f(x)\)与\(f'(x)\)在\((0,+∞)\)上的变化情况如下：
| \(x\) | \(\left(0, \dfrac{1}{a}\right)\) | \(\dfrac{1}{a}\) | \(\left(\dfrac{1}{a}, \dfrac{1}{2}\right)\) | \(\dfrac{1}{2}\) | \(\left(\dfrac{1}{2},+\infty\right)\) |
|---|---|---|---|---|---|
| \(f'(x)\) | \(+\) | \(0\) | \(-\) | \(0\) | \(+\) |
| \(f(x)\) | \(↗\) | \(↘\) | \(↗\) |
所以\(f(x)\)在 \(\left(0, \dfrac{1}{a}\right)\)， \(\left(\dfrac{1}{2},+\infty\right)\)内单调递增，在\(\left(\dfrac{1}{a}, \dfrac{1}{2}\right)\)内单调递减．
综上所述，
当\(a≤0\)时，\(f(x)\)在\(\left(0, \dfrac{1}{2}\right)\)内单调递增，在 \(\left(\dfrac{1}{2},+\infty\right)\)内单调递减；
当\(0<a<2\)时，\(f(x)\)在\(\left(0, \dfrac{1}{2}\right)\)，\(\left(\dfrac{1}{a},+\infty\right)\)内单调递增，在\(\left(\dfrac{1}{2}, \dfrac{1}{a}\right)\)内单调递减；
当\(a=2\)时，所以\(f(x)\)在\((0,+∞)\)上单调递增；
当\(a>2\)时，\(f(x)\)在 \(\left(0, \dfrac{1}{a}\right)\)， \(\left(\dfrac{1}{2},+\infty\right)\)内单调递增，在\(\left(\dfrac{1}{a}, \dfrac{1}{2}\right)\)内单调递减．
- 答案 当\(a≥0\)时，\(f(x)\)在\((-∞,-1)\)递减，在\((-1,+∞)\)递增，
当\(-\dfrac{1}{e}<a<0\)时，\(f(x)\)在\((\ln (-a),-1)\)递减，在\((-∞,\ln (-a))\),\((-1,+∞)\)递增，
当\(a=-\dfrac{1}{e}\)时，\(f(x)\)在\(R\)递增，
当\(a<-\dfrac{1}{e}\)时，\(f(x)\)在\((-1,\ln (-a))\)递减，在\((-∞,-1)\),\((\ln (-a),+∞)\)递增.
解析 \(f'(x)=ax+e^x+xe^x+a=e^x (x+1)+a(x+1)=(x+1)(e^x+a)\)，
(1)若\(a≥0\)时，\(e^x+a>0\)
当\(x<-1\)时，\(f'(x)<0\)；当\(x>-1\)时，\(f'(x)>0\)；
(2)若\(a<0\)时，由\(f'(x)=0\)，解得\(x_1=-1\)或\(x_2=\ln (-a)\)，
①若\(a=-\dfrac{1}{e}\)时，则\(\ln (-a)=-1⇒x_1=x_2\)，\(f'(x)≥0\)恒成立，故\(f(x)\)在\(R\)递增；
②若\(-\dfrac{1}{e}<a<0\)，则\(\ln (-a)<-1⇒x_1<x_2\)，
当\(\ln (-a)<x<-1\)时，\(f'(x)<0\)，\(f(x)\)递减；
当\(x<\ln (-a)\)或\(x>-1\)时，\(f'(x)>0\)，\(f(x)\)递增.
③若\(a<-\dfrac{1}{e}\)，则\(\ln (-a)>-1⇒x_1>x_2\)，
当\(-1<x<\ln (-a)\)时，\(f'(x)<0\)，\(f(x)\)递减；
当\(x<-1\)或\(x>\ln (-a)\)时，\(f'(x)>0\)，\(f(x)\)递增.
综上，
当\(a≥0\)时，\(f(x)\)在\((-∞,-1)\)递减，在\((-1,+∞)\)递增，
当\(-\dfrac{1}{e}<a<0\)时，\(f(x)\)在\((\ln (-a),-1)\)递减，在\((-∞,\ln (-a))\),\((-1,+∞)\)递增，
当\(a=-\dfrac{1}{e}\)时，\(f(x)\)在\(R\)递增，
当\(a<-\dfrac{1}{e}\)时，\(f(x)\)在\((-1,\ln (-a))\)递减，在\((-∞,-1)\),\((\ln (-a),+∞)\)递增.
【B组---提高题】
1.函数 \(f(x)=x-\dfrac{2 a}{x}-(a+2) \ln x\)的单调区间.
2.求\(g(x)=e^x+\cos x-ax-2(x≥0)\)的单调性.
参考答案
-
答案 当\(a<0\)时，\(f(x)\)递减区间为\((0,2)\)，\(f(x)\)递增区间为\((2,+∞)\)；
当\(a=2\)时，\(f(x)\)递增区间为\((0,+∞)\)；
当\(a>2\)时，\(f(x)\)递增区间为\((0,2)\)或\((a,+∞)\)，\(f(x)\)递减区间为\((2,a)\)；
当\(0<a<2\)时，\(f(x)\)递增区间为\((0,a)\)或\((2,+∞)\)，\(f(x)\)递减区间\((a,2)\).
解析 \(f(x)\)的定义域为\((0,+∞)\)，
\(f^{\prime}(x)=1+\dfrac{2 a}{x^2}-\dfrac{a+2}{x}=\dfrac{x^2-(a+2) x+2 a}{x^2}=\dfrac{(x-2)(x-a)}{x^2}\)，
(求导后通分、因式分解，确保有零点存在)
令\(f'(x)=0\)，得\(x_1=2\),\(x_2=a\)，
(对导函数零点\(2\)、\(a\)与定义域端点\(0\)三者比较大小，先比较\(a\)与\(0\)的大小，分\(a>0\)和\(a≤0\))
(1)若\(a≤0\)时，
当\(0<x<2\)时，\(f'(x)<0\)，\(f(x)\)递减；
当\(x>2\)时，\(f'(x)>0\)，\(f(x)\)递增；
(2)若\(a>0\)时，
(判断导函数零点\(2\)、\(a\)的大小，分\(a=2\)、\(a>2\)、\(a<2\)三种情况)
①\(a=2\)时，\(f'(x)=(x-2)^2≥0\)，\(f(x)\)递增;(不要遗忘零点相等的情况)
②\(a>2\)时，
当\(0<x<2\)或\(x>a\)时，\(f'(x)>0\)，\(f(x)\)递增；
当\(2<x<a\)时，\(f'(x)<0\)，\(f(x)\)递减；
③\(0<a<2\)时，
当\(0<x<a\)或\(x>2\)时，\(f'(x)>0\)，\(f(x)\)递增；
当\(a<x<2\)时，\(f'(x)<0\)，\(f(x)\)递减.
综上所述
当\(a<0\)时，\(f(x)\)递减区间为\((0,2)\)，\(f(x)\)递增区间为\((2,+∞)\)；
当\(a=2\)时，\(f(x)\)递增区间为\((0,+∞)\)；
当\(a>2\)时，\(f(x)\)递增区间为\((0,2)\)或\((a,+∞)\)，\(f(x)\)递减区间为\((2,a)\)；
当\(0<a<2\)时，\(f(x)\)递增区间为\((0,a)\)或\((2,+∞)\)，\(f(x)\)递减区间\((a,2)\). -
答案 当\(a≤1\)时，\(g(x)\)在\([0,+∞)\)上单调递增；
当\(a>1\)时，\(g(x)\)在\([0,+∞)\)上先减后增.
解析 \(g'(x)=e^x-\sin x-a\)，
令\(p(x)=g'(x) =e^x-\sin x-a\)，故\(p'(x)=e^x-\cos x\)，
当\(x≥0\)时，\(p'(x)≥0\)，故\(p(x)\)在\([0,+∞)\)上单调递增，
(要注意三角函数\(\sin x\)、\(\cos x\)的范围\([-1 ,1]\))
(此时 \(p(x)_{\min }=p(0)=1-a\)，分析导函数是否有零点，分\(1-a≤0\)和\(1-a>0\)讨论.)
①当\(a≤1\)时，\(p(x)≥p(0)=1-a≥0\)，即\(g'(x)≥0\)，
故\(g(x)\)在\([0,+∞)\)上单调递增；
②当\(a>1\)时，\(p(0)=1-a<0\)，且\(p(\ln (a+1))=1-\sin (\ln a(a+1))≥0\)，
故存在\(x_0∈(0,\ln (a+1)]\)，使得\(p(x_0)=g'(x_0)=0\)，
当\(0<x<x_0\)时，\(g'(x)<0\)，\(g(x)\)单调递减；
当\(x>x_0\)时，\(g'(x)>0\)，\(g(x)\)单调递增.
综上所述，当\(a≤1\)时，\(g(x)\)在\([0,+∞)\)上单调递增；
当\(a>1\)时，\(g(x)\)在\([0,+∞)\)上先减后增.
【C组---拓展题】
1.已知函数\(f(x)=e^x- \dfrac{1}{2} ax^2-x\)．
(1)设\(f'(x)\)是\(f(x)\)的导函数，讨论函数\(y=f'(x)\)的单调性；
(2)当\(a≤1-\dfrac{1}{e}\)时，求证：\(f(x)+x-\ln (x+1)≥1\)．
参考答案
- 答案 (1)当\(a≤0\)时，\(y=f'(x)\)是\((-∞,+∞)\)上的增函数，
当\(a>0\)时，\(y=f'(x)\)在\((-∞,\ln a)\)是减函数，在\((\ln a,+∞)\)上是增函数．
(2)略.
解析 (1)由已知\(f'(x)=e^x-ax-1\)，
设\(g(x)=f'(x)=e^x-ax-1\)，则\(g'(x)=e^x-a\)，
①当\(a≤0\)时，\(g'(x)=e^x-a>0\)在\(R\)上恒成立，
所以\(g(x)=f'(x)=e^x-a>0\)在\(R\)上恒成立，
所以\(g(x)=f'(x)\)在\((-∞,+∞)\)上单调递增，
②当\(a>0\)时，令\(g'(x)>0\)得\(x>\ln a\)，\(g'(x)<0\)得\(x<\ln a\)，
所以\(g(x)=f'(x)\)在\((-∞,\ln a)\)上单调递减，在\((\ln a,+∞)\)上单调递增，
综上所述，当\(a≤0\)时，\(y=f'(x)\)是\((-∞,+∞)\)上的增函数，
当\(a>0\)时，\(y=f'(x)\)在\((-∞,\ln a)\)是减函数，在\((\ln a,+∞)\)上是增函数．
(2)由(1)知，①当\(a≤0\)时，\(f'(x)=e^x-ax-1\)在\((-1,+∞)\)上单调递增，
又\(f'(0)=0\)，
所以\(-1<x<0\)时，\(f'(x)<0\)；\(x>0\)时，\(f'(x)>0\)，
则\(f(x)\)在\((-1,0)\)上单调递减，在\((0,+∞)\)上单调递增，
所以 \(f(x)_{\min }=f(0)=1\)，
②当\(0<a≤\dfrac{1}{e}\)时\(，\ln a≤-1\)，
由(1)知\(f'(x)\)在\((-1,+∞)\)上单调递增，又\(f'(0)=0\)，
则\(f(x)\)在\((-1,0)\)上单调递减，在\((0,+∞)\)上单调递增，
所以 \(f(x)_{\min }=f(0)=1\)，
③当\(\dfrac{1}{e}<a≤1-\dfrac{1}{e}\)时，
由(1)知\(f'(x)\)在\((-1,\ln a)\)上单调递减，在\((\ln a,+∞)\)上单调递增，
且\(f'(0)=0\)，\(f'(-1)=\dfrac{1}{e}+a-1≤0\)，
所以\(-1≤x<0\)时，\(f'(x)<0\)；\(x>0\)时，\(f'(x)>0\)，
所以\(f(x)\)在\((-1,0)\)上单调递减，在\((0,+∞)\)单调递增，
则 \(f(x)_{\min }=f(0)=1\)，
综上所述：函数\(f(x)\)在\([-1,+∞)\)上的最小值为\(1\)，
所以\(f(x)≥1\)，
要证明原不等式只需证明\(x-\ln (x+1)≥0\)，
设\(h(x)=x-\ln (x+1)(x>-1)\)，
所以 \(h^{\prime}(x)=1-\dfrac{1}{x+1}=\dfrac{x}{x+1}\)，
则当\(-1<x<0\)时，\(h'(x)<0\)；\(x>0\)时，\(h'(x)>0\)，
即\(h(x)\)在\((-1,0)\)上单调递减，在\((0,+∞)\)上单调递增，
则 \(h(x)_{\min }=h(0)=0\)，即\(x-\ln (x+1)≥0\)，
又\(f(x)≥1\)，
故\(f(x)+x-\ln (x+1)≥1\)．