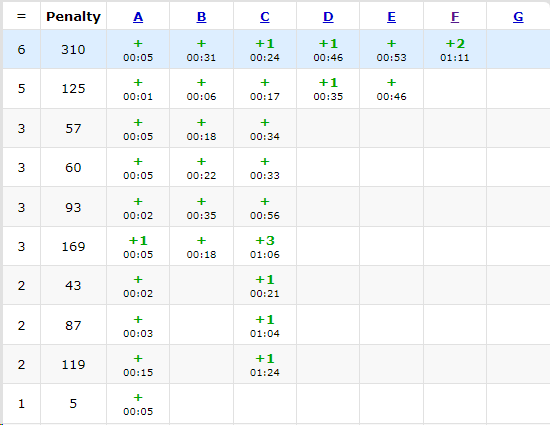
(逆天罚时局)
复盘
看 A,一眼简单题。如果先手拿到的就是 \(3\) 的倍数,则后手必胜,否则先手可以只走一步达成 \(3\) 的倍数(最开始我还想反了,导致 00:05)。
不想开 B,看 C,我相信它有更简单的解法但我 dp 也能过。
B 马上切了没什么好说的。
D 直接分析一句话题意,然后用函数胡一下,发现整点只有两个于是就切了(没 long long WA 了一发)。
E 分析样例直接取最小值位置且最小值后面不能递减,然后过了,我感觉 E 是最简单的一道。
开 F 以为是一道史诗构造题结果分析一下是个诈骗题。
最开始以为可以构造满二叉树,但是满二叉树的直径是 \(\log\) 级别的,直接老实了。
然后继续分析特例(一般的构造都是这么分析的),发现链的性质很不错,写写交了。
WA 了一发是因为没有更新特殊点,还有一发是因为构造树的时候输出没有换行。
罚时高到如果 rk2 比赛结束后半小时过 F 都能超过我……
题解
A
唐诗题目,如果 \(n \bmod 3 = 0\) 无论先手怎么走后手都可以一步走回去,然后反复折磨超过 \(10\) 回合,后手必胜。
否则先手一步就能走到正确位置,先手必胜。
B
bf 不说了。
C
记 \(dp(i)\) 为前 \(i\) 项中最大子段和,随便转移转移就过了。
D
一句话题意:
求序列 \(a\) 中满足以下条件的 \((i, j)\) 对的个数:
\[(2^{a_i})^{(2^{a_j})} = (2^{a_j})^{(2^{a_i})} \]化简式子:
\[2^{a_i \times 2 ^ {a_j}} = 2^{a_j \times 2 ^ {a_i}}\\ a_i \times 2 ^ {a_j} = a_j \times 2 ^ {a_i} \\ \frac{a_i}{a_j} = \frac{2 ^ {a_i}}{2 ^ {a_j}} \]画出图像 \(\frac{x}{y} = \frac{2 ^ {x}}{2 ^ {y}}\) 图像:
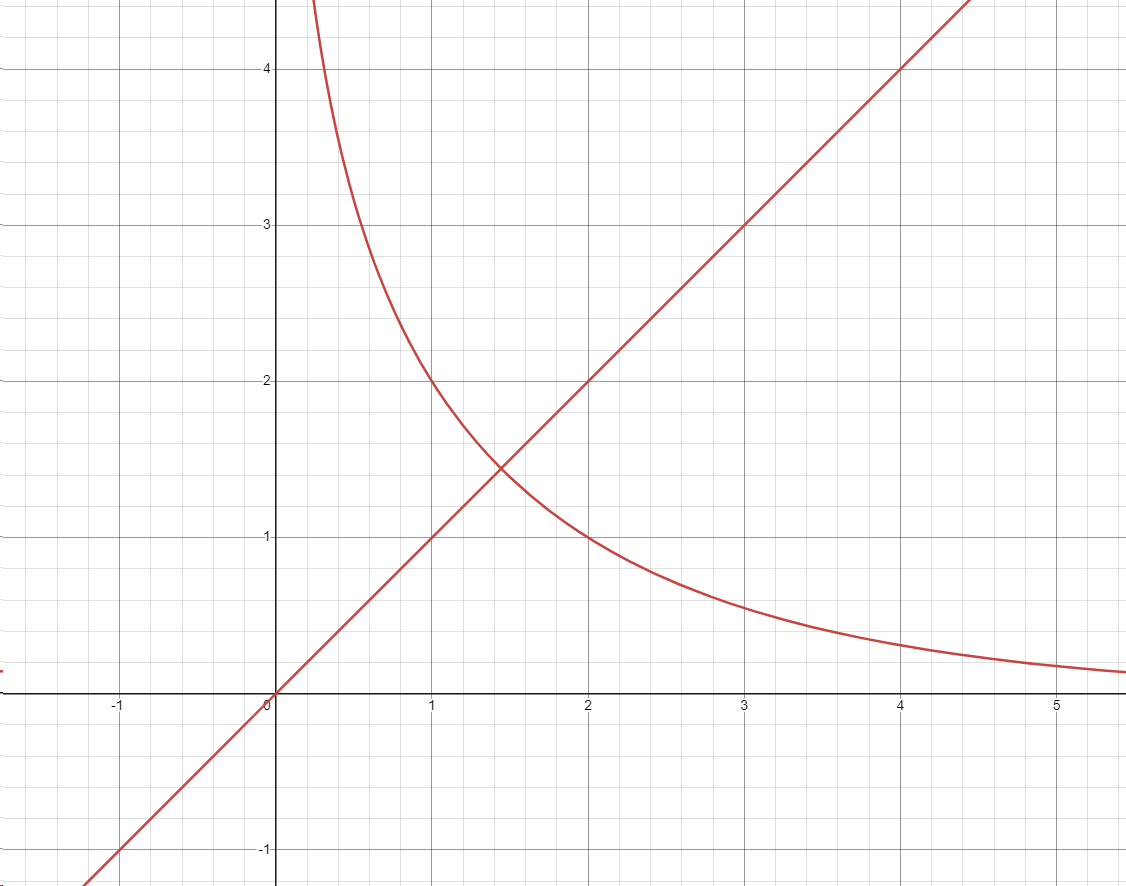
发现该图像由 \(y = x\) 和一个类似 \(y = \frac{2}{x}\) 的拼凑而成。
除了 \(y = x\) 以外只有 \((1, 2)\) 和 \((2, 1)\) 两个整点,特判一下即可。
E
首先操作次数显然不能大于 \(n\)。
接着我们发现它的操作次数为最小值位置减 \(1\)。
但是最小值的后面必须单调不降。
维护一下即可(以上基本由分析样例得到)。
F
构造一条链 \(1 \to n\),每次挪动 \(n\),将 \(n\) 节点作为叶节点,不断更改与 \(1\) 之间的距离,如果距离恰好为 \(d\) 就输出 -1 -1 -1,否则输出 n dis(1, n) d(可以自行理解,这里不赘述)。