标签：乱讲 水题 limits dfrac sum j1 times le

一大堆错，别喷了。

前言

下图取自某人的 PPT，有删改。

题面

APIO2014 序列分割

题目大意

你正在玩一个关于长度为 \(n\) 的非负整数序列的游戏，第 \(i\) 个位置的值为 \(a_i\)。

这个游戏中你需要把序列分成 \(k + 1\) 个非空的块，为了得到 \(k + 1\) 块，你需要重复下面的操作 \(k\) 次：

• 选择一个有超过一个元素的块（初始时你只有一块，即整个序列）。

• 选择两个相邻元素把这个块从中间分开，得到两个非空的块。

每次操作后你将获得那两个新产生的块的元素和的乘积的分数，你想要最大化最后的总得分。

数据范围

\(2 \le n \le 10^5\)，\(1 \le k \le \min\{n - 1, 200\}\)。

闲话：pjt 问我 T1 是什么，我说是动态规划板子，这很合理。

CF1517G Starry Night Camping

题目大意

有 \(n\) 顶帐篷，第 \(i\)个帐篷位于点 \((x_i, y_i)\) 上，权值为 \(w_i\)。当且仅当 \(x_i\) 和 \(y_i\) 都是偶数时，帐篷 \(i\) 才是重要的。

移除一些帐篷，使得对于每个剩余的重要帐篷 \((x, y)\)，不存在另外 \(3\) 个帐篷 \((x' _ 1, y' _ 1),(x' _ 2, y' _ 2)\) 和 \((x' _ 3, y' _ 3)\)，使得以下两个条件都成立：

• \(|x'_j-x|,|y'_j-y|\le 1\)，对于所有 \(j\in\{1,2,3\}\)。

• 这四个帐篷形成一个平行四边形（或矩形），它的一条边平行于 \(x\) 轴。

将未移走的帐篷权值之和最大化，输出最大值。

数据范围

\(1\le n\le 1000\)，\(-10^9\le x_i,y_i\le 10^9\)，\(1\le w_i\le 10^9\)。

CF1983E I Love Balls

题目大意

Alice 和 Bob 在玩游戏。他们面前有 \(n\) 个球，第 \(i\) 个球的价值为 \(v_i\)，且前 \(k\) 个球为“特殊球”，Alice 为先手。

每一轮，Alice 或 Bob 会随机从剩余的球中选取一个球并把它取出，获得它的价值。

如果这个球为特殊球，则下一轮的玩家不变，否则下一轮的玩家改变。

问 Alice 和 Bob 各自得到的价值的期望对 \(10^9 + 7\) 取模的值。

数据范围

多测，\(1\le T\le 2\times 10^5\)，\(1\le k\le n\le 4\times 10^5\)，\(1\le v_i\le 10^7\)。

CEOI2017 Building Bridges

有 \(n\) 根柱子依次排列，每根柱子都有一个高度。第 \(i\) 根柱子的高度为 \(h_i\)。

现在想要建造若干座桥，如果一座桥架在第 \(i\) 根柱子和第 \(j\) 根柱子之间，那么需要 \((h_i-h_j)^2\) 的代价。

在造桥前，所有用不到的柱子都会被拆除，因为他们会干扰造桥进程。第 \(i\) 根柱子被拆除的代价为 \(w_i\)，注意 \(w_i\) 不一定非负，因为可能政府希望拆除某些柱子。

现在政府想要知道，通过桥梁把第 \(1\) 根柱子和第 \(n\) 根柱子连接的最小代价。注意桥梁不能在端点以外的任何地方相交。

数据范围

\(2\le n\le 10^5\)，\(0\le h_i,\vert w_i\vert\le 10^6\)。

CF1278F Cards 加强

题目大意

有 \(m\) 张牌，其中一张是王牌。

现在你执行 \(n\) 次右侧操作：洗牌后查看第一张牌是什么。

令 \(x\) 为洗牌后第一张牌为王牌的次数，现在假设洗牌时 \(m!\) 种牌的排列出现的概率均相等，求 \(x^k\) 的期望值，答案对 \(998244353\) 取模。

数据范围

\(1\le n,m\le 998244353\)，\(1\le k\le 10^7\)。

闲话：本来的范围 \(k\le 5000\)。

gym 102331 J Jiry Matchings

题目大意

给定一棵树 \(n\) 个节点的有边权的树，求对于 \(k\in[1,n]\cap\mathbb{Z}\) 的大小为 \(k\) 的匹配的最大权值。

一个图的匹配就是在一张图上选择一些边，要求这些边没有公共的端点。

数据范围

\(1\le n\le 2\times 10^5\)，时限 \(2s\)。

solution

APIO2014 序列分割

容易得到一个性质：

同样的切法得到的答案都是一样的，换而言之切的顺序与答案无关。

容易证明，设我们把三段和为 \(D,C,Z\) 的三段切开，那么：

• 先切 \(C,Z\) 的贡献为：\((D+C)\times Z+D\times C\)，也就是 \(DC+DZ+CZ\)。
• 先切 \(D,C\) 的贡献为：\(D\times (C+Z)+C\times Z\)，也就是 \(DC+DZ+CZ\)。

设 \(s_i=\sum\limits_{i=1}^i a_i\)，\(F_{i,j}\) 表示前 \(i\) 次切割 \(j\) 次可以得到的贡献的最大值，注意这个的状态数是 \(O(nk)\) 的如果 \(O(1)\) 转移是可以通过的。

我们记 \(f_k=F_{i,k}\)，\(g_k=F_{i-1,k}\)，那么显然有转移方程：

\[f_i=\max\{g_j+s_j\times (s_i-s_j)\} \]

显然添加的第 \([i,j]\) 段会和前面所有的段都发生贡献，所以需要乘以 \(s_j\)。

观察，Z_drj 都可以看出来可以斜率优化。

我们取任意的 \({j1}\lt {j2}\) 且满足 \(f_i\) 的决策点是 \({j2}\) 优于 \({j1}\)，那么就可以得到下面的不等式：

\[g_{j2}+s_{j2}\times (s_i-s_{j2})\gt g_{{j1}}+s_{{j1}}\times (s_i-s_{j1}) \]

整理一下得到：

\[(s_i\times s_{j2})+(g_{{j2}}-{s_{{j2}}}^2)\gt (s_i\times s_{j1})+(g_{{j1}}-{s_{{j1}}}^2) \]

移项：

\[s_i\times (s_{j2}-s_{j1})\gt g_{{j1}}-{s_{{j1}}}^2-g_{{j2}}+{s_{{j2}}}^2 \]

因为 \(s_{j2}\gt s_{j1}\)，所以有：

\[-s_i\lt \dfrac{(g_{{j2}}+{s_{{j2}}}^2)-(g_{{j1}}-{s_{{j1}}}^2)}{s_{j2}-s_{j1}} \]

总结一下，如果上面的式子成立那么 \(j2\) 比 \(j1\) 要优。

考虑建立一个直角坐标系，把 \(s\) 作为 \(X\) 坐标，把 \(g+s^2\) 作为 \(Y\) 坐标，那么每一个决策就都成为了一个点。

假设有三个决策点 \(D,C,Z\)，他们的斜率分别是 \(k_1\) 和 \(k_2\)，且 \(k_0\) 是 \(-s_i\)，满足下图：

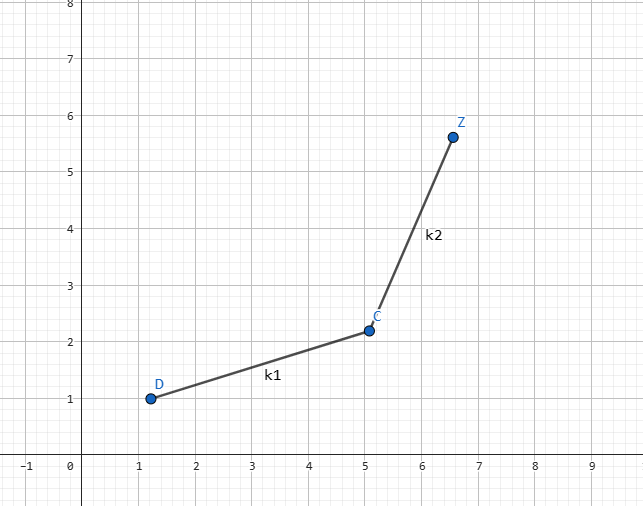
那么根据我们上面得到的式子有：

• 如果 \(k_0<k_1\)，那么 \(C\) 比 \(D\) 优。
• 如果 \(k_0<k_2\)，那么 \(Z\) 比 \(C\) 优。
• 观察得到 \(k_1<k_2\)，即上图是一个下凸。

那么有三种情况：

• \(k_0<k_1<k_2\)，那么 \(Z\) 比 \(C\)，\(D\) 优。
• \(k_1<k_0<k_2\)，那么 \(D\)，\(Z\) 比 \(C\) 优。
• \(k_1<k_2<k_0\)，那么 \(D\) 比 \(C\)，\(Z\) 优。

发现 \(C\) 太逊了，也就是在这个情况下是决策点永远不可能是下凸。

因为永远不可能是下凸，所以肯定是上凸（好像这句话是废话）。

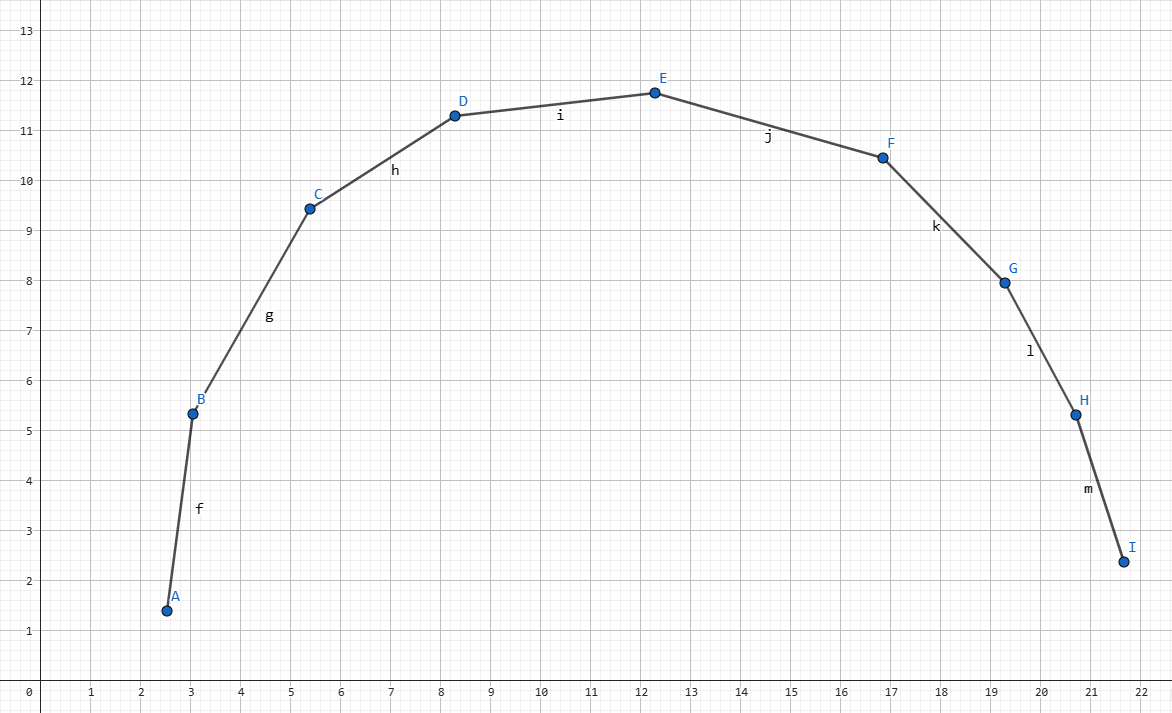
显然，如果决策点 \(k\) 被选择，当且仅当这个点前面的斜率都比 \(k_0\) 小，它后面的点都比他大。

所以瞪眼法可以得到如果蓝线是 \(k_0\) 那么 \(D\) 就是决策点。

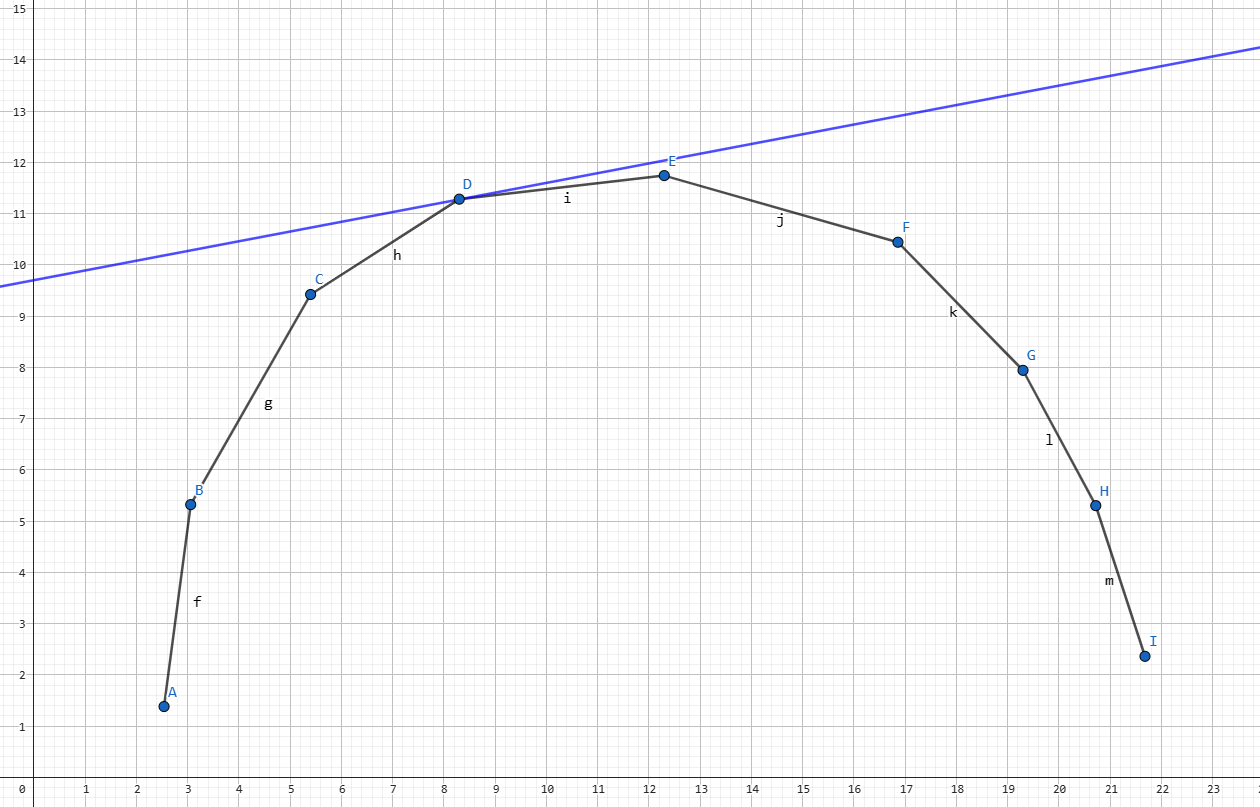
考虑这个东西怎么维护，发现新加入的点的斜率都是 \(X\) 坐标都是单调的，那么显然可以直接维护一个可以在末尾添加元素的玩意。

因为上凸包的斜率具有单调性，且寻找的是第一个大于的点，所以可以二分查找，转移的时间复杂度是 \(O(\log n)\) 的。

但是发现这个题目的 \(k_0\) 也是递增的，所以其实比 \(k_0\) 小的以后都不会取到，所以可以直接在末尾弹出元素。

所以最后的时间复杂度为 \(O(nk)\)，就是一个斜率优化的板子，让某些人复习或者预习一下。

CF1517G Starry Night Camping

将节点的 \(x_i,y_i\) 的奇偶性划分成 \(A,B,C,D\) 四个集合，注意相邻集合在图中需要时可以满足 \(\operatorname{dist}\) 为 \(1\) 的。

容易发现对于一个不合法的四边形，一定满足四个帐篷之间的切比雪夫距离均为 \(1\) 而且四个点分别属于 \(A,B,C,D\) 四个集合。

每一种帐篷只有选择或者不选择，考虑使用最小割进行求解。

因为帐篷 \(u\) 无法在最小割中被删除，考虑将 \(u\) 拆为两个节点 \(u_1,u_2\) 并用权值为 \(w_u\) 的边链接 \(u_1,u_2\)，如果将边 \(u_1\to u_2\) 删除，那么就意味着帐篷 \(u\) 被放弃掉了。

考虑将集合编号相邻且在图上曼哈顿距离为 \(1\) 的节点之间连边，具体的要将编号小的 \(x_2\) 向集合编号较大的 \(y_1\) 连边边权为 \(inf\) 的边。

最后将 \(A\) 集合内的所有点与 \(S\) 连边，将 \(D\) 集合内所有的点与 \(T\) 连边，边权都是 \(inf\)。

显然，如果节点 \(a,b,c,d\) 是不合法的帐篷，那么它们显然会被边权为 \(inf\) 的边全部连接起来，那么只有割掉任意一条边权不为 \(inf\) 的边才可以使 \(S,T\) 不连通。根据上面的解释，这也就是放弃了一个帐篷。

时间复杂度为 \(O(n^3)\)，但是是网络流。

CF1983E I Love Balls

定义一般球被 Alice 拿出的期望次数和平均值分别为 \(p_1,s_1\)，特殊球为 \(p_2,s_2\)，那么显然 Alice 拿出的球的期望为 \(p_1s_1+p_2s_2\)。

因为 Alice 和 Bob 会等概率的拿球，所以 \(s_1,s_2\) 就是一般球与特殊球权职和的平均。

考虑没有特殊球的情况，如果将普通球排成一列两个玩家一次取出，显然这样的期望值与题目描述的一样。

但是题目插入了 \(k\) 个特殊球，可以理解为将原本的序列分成的几段，每一段只有在最后包含了一个普通球或者不包含，每一个玩家一次取出一段。

发现插入特殊球并没有影响玩家取出普通球的个数，可以得到 \(p_1=\lfloor \dfrac{n-k+1}{2}\rfloor\)。

显然 Alice 遇到的缝隙的数量是 \(\lfloor \dfrac{n-k+2}{2}\rfloor\)，每一个缝隙中遇到的球的期望是 \(\dfrac{k}{n-k+1}\)，所以 \(p_2=\dfrac{k\cdot \lfloor \dfrac{n-k+2}{2}\rfloor}{n-k+1}\)。

CEOI2017 Building Bridges

设 \(s_i=\sum\limits_{j=1}^i w_i\)，考虑前 \(i\) 个柱子并且保留第 \(i\) 个柱子的最小代价。

那么有容易想到朴素的转移方程：

\[f_{i}=\min\{f_j+s_{i-1}-s_j+(h_i-h_j)^2\} \]

考虑把这个玩意展开，得到：

\[f_j+s_{i-1}-s_j+{h_i}^2+{h_j}^2-2\times h_ih_j \]

发现出现了乘积项，考虑使用斜率优化。

注意，因为 \(w_i\) 有负数所以 \(h_i\) 不再递增了。

考虑如果 \(h\) 递增，那么下面的分析会假设 \(j1<j2\) 以得到 \(h_{j1}<h_{j2}\) 来移项，但是实际上我们并没有直接的使用 \(j1\) 和 \(j2\) 之间的大小关系。

所以我们可以换一种假设方式，假设 \(h_{j1}<h_{j2}\) 且 \(j2\) 比 \(j1\) 优。

套路的可以得到不等式：

\[(-2\times h_ih_{j1})+(f_{j1}-s_{j1}+{h_{j1}}^2)+(s_{i-1}+{h_i}^2)>(-2\times h_ih_{j2})+(f_{j2}-s_{j2}+{h_{j2}}^2)+(s_{i-1}+{h_i}^2) \]

移项得到：

\[2h_i\times (h_{j2}-h_{j1})>(f_{j2}-s_{j2}+{h_{j2}}^2)-(f_{j1}-s_{j1}+{h_{j1}}^2) \]

因为有 \(h_{j1}<h_{j2}\)，所以如果按照 \(h\) 排序之后满足下式就可以得到 \(j2\) 比 \(j1\) 优：

\[2h_i>\dfrac{(f_{j2}-s_{j2}+{h_{j2}}^2)-(f_{j1}-s_{j1}+{h_{j1}}^2)}{(h_{j2}-h_{j1})} \]

容易发现应该维护下凸壳，考虑让强行让 \(h\) 单调。

考虑分治，先处理左区间，然后再用左区间得到的结果处理右区间。

具体的，把左右区间分别递归完之后再归并排序即可，时间复杂度为 \(O(n\log n)\)。

另外有人发现这是 CDQ 分治吗？

CF1278F Cards 加强

定义 \(f_i\) 表示有将 \(i\) 个不同的元素组成的特定结构的方案数，\(g_i\) 表示从 \(i\) 个元素任意选出一些（可以不选）组成特定结构的方案数。

对于知道 \(f_i\) 或者 \(g_i\) 中的任意一个就可求解另外一个，其公式如下：

\[g_n=\sum\limits_{i=0}^n{n\choose i}f_i \]

\[f_{n}=\sum\limits_{i=0}^n{n\choose i}(-1)^{n-i}g_i \]

就是容斥，直接感性理解，相信 ljw 在讲组合数的时候会讲的。

发现有人不会斯特林数，\(\begin{Bmatrix}n\\ k\end{Bmatrix}\) 表示把 \(n\) 个两两不同的元素，划分为 \(k\) 个互不区分的非空子集的方案数。

简单讲一下怎么求通项公式：

设 \(G_i\) 表示将 \(n\) 个不同元素放入 \(i\) 个不同盒子允许为空的方案数，\(F_i\) 表示将 \(n\) 个不同的元素放入 \(i\) 个不同盒子不允许为空的方式。

那么显然：

\[G_i=i^n \]

同时还有：

\[G_i=\sum\limits_{j=0}^i {i\choose j} F_j \]

发现上面的式子和二项式反演一样，所以得到：

\[F_i=\sum\limits_{j=0}^i (-1)^{i-j}\times {i\choose j}\times G_i \]

将 \(G\) 带入并化简得到：

\[F_i=\sum\limits_{j=0}^i\dfrac{(-1)^{i-j}\times i!\times i^n}{j!\times (i-j)!} \]

因为斯特林数的盒子不一样，所以 \(F_k\) 就是就是 \(\begin{Bmatrix}n\\ k\end{Bmatrix}\) 的 \(k!\) 倍，所以得到：

\[\begin{Bmatrix}n\\ k\end{Bmatrix}=\dfrac{F_k}{k!}=\sum\limits_{i=0}^k\dfrac{(-1)^{k-i}\times i^n}{i!\times (k-i)!} \]

得到：

\[i^n=\sum\limits_{j=0}^i j!\times {i\choose j}\times \begin{Bmatrix} n\\j\end{Bmatrix} \]

把组合数展开然后约分得到：

\[i^n=\sum\limits_{j=1}^i \dfrac{i!}{(i-j)!}\times \begin{Bmatrix} n\\j\end{Bmatrix} \]

记抽出王牌的概率 \(\dfrac{1}{m}\) 为 \(p\)，那么按照题目的要求写出式子：

\[\sum\limits_{i=0}^n{n\choose i}p^i(1-p)^{n-i}i^k \]

把 \(i^k\) 根据套路写成第二类斯特林数的形式：

\[\sum\limits_{i=0}^n {n\choose i}p^i(1-p)^{n-i}\sum\limits_{k=0}^{j}\begin{Bmatrix}k\\ j\end{Bmatrix}i^{\underline{j}} \]

其中 \(i^{\underline{j}}\) 表示 \(\dfrac{i!}{(i-j)!}\)，oi-wiki 里面总计了一些常用的符号。

因为 \(n\) 太大了不可以接受，所以考虑把里面的循环提到外面去。

\[\sum\limits_{j=0}^k \begin{Bmatrix}k\\ j\end{Bmatrix}\sum\limits_{i=0}^n{n\choose i}i^{\underline{j}}p^i(1-p)^{n-i} \]

展开得到：

\[\sum\limits_{j=0}^k\begin{Bmatrix}k\\ j\end{Bmatrix}\sum\limits_{i=1}^n\dfrac{i!}{(i-j)!}\dfrac{n!}{i!(n-i)!}p^i(1-p)^{n-i} \]

那么合理组合得到：

\[\sum\limits_{j=0}^k\begin{Bmatrix}k\\ j\end{Bmatrix}\sum\limits_{i=1}^n\dfrac{(n-j)!}{(i-j)!\times (n-i)!}\times \dfrac{n!}{(n-j)!}\times p^i(1-p)^{n-i} \]

考虑组合意义得到：

\[\sum\limits_{j=0}^k\begin{Bmatrix}k\\ j\end{Bmatrix}n^{\underline j}\sum\limits_{i=1}^n{n-j\choose i-j}p^i(1-p)^{n-i} \]

发现上面的组合数太丑陋了，把 \(i-j\) 替换为 \(i\) 得到：

\[\sum\limits_{j=0}^k\begin{Bmatrix}k\\ j\end{Bmatrix}n^{\underline j}\sum\limits_{i=0}^{n-j}{n-j\choose i}p^{i-j}(1-p)^{n-(i-j)} \]

观察式子发现和二项式定理很像：

\[(a+b)^n=\sum\limits_{i=0}^n {n\choose i}a^{i}b^{n-i} \]

把 \(p^i\) 提出来，带入上式得到：

\[\sum\limits_{j=0}^k \begin{Bmatrix}k\\ j\end{Bmatrix}n^{\underline j}p^j (p+1-p)^{n-i} \]

也就是：

\[\sum\limits_{j=0}^k \begin{Bmatrix}k\\ j\end{Bmatrix}\dfrac{n!}{(n-j)!}p^j \]

这时可以 \(O(k^2)\) 朴素求解斯特林数，也可以只用卷积做到 \(O(k\log k)\) 求解，但是还是无法做到线性求解。

把通项公式带入上式：

\[\sum_{i=0}^k\dfrac{n^{\underline{i}}p^i}{i!}\sum_{j=0}^i(-1)^{i-j}\binom{i}{j}j^k \]

交换求和的顺序：

\[\sum_{j=0}^k(-1)^{j}j^k\sum_{i=j}^k\dfrac{n^{\underline{i}}(-p)^i}{i!}\binom{i}{j} \]

展开组合数：

\[\sum\limits_{j=0}^k(-1)^jj^k\sum\limits_{i=j}^k \dfrac{n^{\underline{i}}(-p)^i}{i!}\times \dfrac{i!}{j!(i-j)!} \]

整理一下：

\[\sum_{j=0}^k\dfrac{(-1)^{j}j^k}{j!}\sum_{i=j}^k\dfrac{n^{\underline{i}}(-p)^i}{(i-j)!} \]

和上面的套路同样的，把 \(i\) 替换为 \(i+j\) 得到：

\[\sum\limits_{j=0}^k\dfrac{(-1)^jj^k}{j!}\sum\limits_{i=0}^{k-j}\dfrac{n^{\underline{i+j}}(-p)^{i+j}}{i!} \]

整理一下得到：

\[\sum_{j=0}^k\dfrac{(-1)^{j}j^k(-p)^j}{j!}\sum_{i=0}^{k-j}\dfrac{n^{\underline{i+j}}(-p)^i}{i!} \]

继续变形得到：

\[\sum_{j=0}^k\dfrac{j^kp^jn!}{j!(n-j)!}\sum_{i=0}^{k-j}\dfrac{(n-j)!}{i!(n-i-j)!}\times (-p)^i \]

考虑组合意义得到：

\[\sum\limits_{j=0}^k\dfrac{j^kp^jn^{\underline j}}{j!}\sum\limits_{i=0}^{k-j}{n-j\choose i}(-p)^i \]

观察上式的第二个 \(\sigma\) 的前面，发现：

• 阶乘和下降阶乘幂显然可以 \(O(k)\) 预处理。
• \(g(x)=p^x\) 显然可以 \(O(k)\) 预处理。
• \(g'(x)=x^k\) 是积性函数，可以通过欧拉筛 \(O(k)\) 预处理。

所以我们只需要在 \(O(k)\) 或者更低的时间复杂度内求解出后面的玩意就可以了。

考虑设函数：

\[f(j)=\sum_{i=0}^{k-j}\binom{n-j}{i}p^i \]

那么容易想到可以去递推求解，那么直接考虑两式的差：

\[\sum_{i=0}^{k-j+1}\binom{n-j+1}{i}p^i-\sum_{i=0}^{k-j}\binom{n-j}{i}p^i \]

那么把可以相像的项写道一起得到：

\[\sum_{i=0}^{k-j}p^i\left[\binom{n-j+1}{i}-\binom{n-j}{i}\right]+\binom{n-j+1}{k-j+1}p^{k-j+1} \]

因为组合数的意义有：

\[\sum_{i=0}^{k-j}p^i\left[{n-j\choose i}+{n-j\choose i-1}-\binom{n-j}{i}\right]+\binom{n-j+1}{k-j+1}p^{k-j+1} \]

整理得到：

\[\sum_{i=0}^{k-j}\binom{n-j}{i-1}p^i+\binom{n-j+1}{k-j+1}p^{k-j+1} \]

同样的处理掉组合数里的 \(i-1\) 得到：

\[p\sum_{i=0}^{k-j-1}\binom{n-j}{i}p^i+\binom{n-j+1}{k-j+1}p^{k-j+1} \]

考虑把 \(f(j)\) 带入上式：

\[p\left[f(j)-\binom{n-j}{k-j}p^{k-j}\right]+\binom{n-j+1}{k-j+1}p^{k-j+1} \]

把式子展开然后提取公因式得到：

\[pf(j)+\left[\binom{n-j+1}{k-j+1}-\binom{n-j}{k-j}\right]p^{k-j+1} \]

根据组合数的性质，类似与上面的化简得到：

\[pf(j)+\binom{n-j}{k-j+1}p^{k-j+1} \]

也就是：

\[f(j-1)-f(j)=pf(j)+\binom{n-j}{k-j+1}p^{k-j+1} \]

消元得到：

\[f(j-1)=(p+1)f(j)+\dfrac{n^{\underline{k+1}}}{n^{\underline{j}}(k-j+1)!}p^{k-j+1} \]

带入容易得到 \(f(\min\{n,k\})=1\)，所以原式就是：

\[\sum_{j=0}^k\dfrac{j^k(-p)^jn^{\underline{j}}}{j!}f(j) \]

注意 \(p\) 的符号变了，记得递推的时候处理。

所有操作的时间复杂度均为 \(O(k)\)，这个问题就解决了。

gym 102331 J Jiry Matchings

做这个题之前需要了解一些前置知识。

定义一个排列是凸序列，当且仅当满足这个序列的差分数组单调不升；反之如果这个序列的差分数组单调不降，那么这个序列就是凹序列。

\(\max/\min,+\) 卷积优化 DP，对于这样的一个转移方程：

\[f_{i}=\max\limits_{j+k=i} g_j+h_k \]

显然这个玩意可以 \(O(n^2)\) 的转移，但是如果 \(g\) 和 \(h\) 都是凸序列，那么就会有更优的做法。

那么把 \(f_0\) 初始化为 \(g_0+h_0\)，然后把两个序列看成：

\[\begin{array}{}g_1-g_0,g_2-g_1,g_3-g_2,\cdots,g_{n}-g_{n-1}\\h_1-h_0,h_2-h_1,h_3-h_2,\cdots,h_{n}-h_{n-1}\end{array} \]

那么求解 \(f_k\) 就相当于在两个序列的开头分别选择一些元素，要求总共选择 \(k\) 个元素，然后加上 \(f_0\)。

因为这两个序列都是上凸的，所以其差分数组是单调不升的，于是贪心的维护两个指针选择最开头的元素中大的那一个就行了，这样也就是可以在 \(O(n)\) 的时间复杂度里求解了。

不知道有没有人听说过闵可夫斯基和。

设在以 \(x\) 为根的子树中，选择 \(i\) 条边且 \(x\) 可以被选择得到的匹配的最大值为 \(f_{x,i}\)。

注意，这里必须是可以选择，否则因为一些神奇的原因 \(f\) 不会是一个凸序列。

类似的，设不被选择的最大值为 \(g_{x,i}\)。

观察发现 \(f_x\) 和 \(g_x\) 都是凸序列，zjk 都不会证你觉得我会吗。

感性理解一下，树是一个二分图，带权的二分图匹配可以转化成费用流，因为是费用流所以可以通过 zjk 都不会的证明得到是一个凸序列。

显然这样有一个暴力的 DP 转移，在合并的时候是一个类似于背包的转移，仔细观察发现是一个 \(\max,+\) 的卷积，刚好可以用凸排列优化，所以我们就可以线性的合并。

但是即使可以线性的合并，但是这样的状态数还是 \(O(n^2)\) 的无法通过，使用分治和树剖优化。

考虑减少状态数，即只求解每一个重链的头的 \(f\) 和 \(g\) 的值。

对于一个重链上的点，先只考虑非重儿子的合并。

考虑递归求解，这样所有的非中儿子的 \(f,g\) 都已经求解出来了。

用 FFT 的思想进行分治，每一次把轻儿子分成两半然后合并。

考虑分析时间复杂度，建出递归树，因为每一次区间长度都会减半所以最多只有 \(\log n\) 层。

通过 \(\max,+\) 卷积合并两个长度为 \(o,p\) 的 \(f,g\) 的时间复杂度显然为 \(O(o+p)\)。

假设所有的轻儿子的 \(f,g\) 的项数之和为 \(m\)，那么一层所需的时间复杂度就是 \(O(m)\)。

因为总共有 \(\log n\) 层，所以显然处理轻儿子所需的时间复杂度为 \(O(m\log n)\)。

通过这个方式合并出轻儿子之后考虑对这个重链上的点进行分治，设 \(h_{l,r,0/1,0,1}\) 表示合并了 \([l,r]\) 这个区间，左右端点是否可以选择得到的 \(f\) 和 \(g\) 的值。

那么同样的如果长度为 \(n\)，那么用类似上面的分治方法就可以做到 \(\log n\) 次合并操作。

因为 \(h_{l,r}\) 的项数并不会多于所有的轻儿子的子树的和，所以我们也可以做到 \(O(m\log n)\) 的合并。

考虑上面的操作，所有的时间复杂度相加得到最终的时间复杂度为 \(O(\sum m\log n)\)。

对于树剖，有性质任意一个点到根节点的所经过的重链数量都不会超过 \(\log n\)。

如果一个节点是重链的开头，那么必然存在一个兄弟节点的大小大于自己，所以这个节点子树的大小至少都会是其父节点的一半。

因为大小每一次都会减半，所以重链最深只会有 \(\log n\) 个，自然一个节点向上遍历遇到的重链也不会超过 \(\log n\) 条。

对于每一个节点，对于 \(\sum m\) 的贡献只会在脱离自己的重链时被计算一次，所以 \((\sum m)=n\log n\)，最终的复杂度也就是 \(O(n\log^2 n)\)。

标签：乱讲,水题,limits,dfrac,sum,j1,times,le
From： https://www.cnblogs.com/liudagou/p/18634262