学习笔记/数学：序理论相关

鉴于这个神（xie）奇（e）的东西在我眼前晃过的次数已经过多了，于是决定系统的学习一下。

本文参考了 OI-Wiki 序理论，并在此基础上增添了很多个人理解，特此鸣谢。

前置知识：集合、基础图论。

二元关系

定义

何为二元关系（binary relation）？感性理解，二元关系就是 function<bool(T1, T2)>，比如说:

• \(\mathbf{R}\) 上的 \(\lt\)，即 less<double>，
• \(\mathbf{N}_+\) 上的 \(\mid\)，即 [](int x, int y){return y % x == 0;}，
• 集合上的 \(\subseteq\)，
• 甚至是 \(\mathbf{Z}\) 上的奇怪东西 [](int x, int y){return x + y >= 10;}……

注意到以上的四个例子都满足 T1\(=\)T2，事实上，这样的二元关系被称为齐次二元关系。

那么我们给出数学上的标准定义：

\(\S\) 二元关系（binary relation）：集合 \(X\) 和集合 \(Y\) 上的一个 二元关系 \(R\) 定义为元组 \((X,Y,G(R))\)，其中：

• \(X\) 称为定义域（domain），
• \(Y\) 称为陪域（codomain），
• \(G(R)\subseteq X\times Y=\{(x,y):x\in X,y\in Y\}\) 称为二元关系 \(R\) 的图（graph）。\(xRy\) 成立当且仅当 \((x,y)\in G(R)\)。

特别的，若 \(X=Y\)，则称该二元关系为齐次二元关系（homogeneous relation）。

下文我们所研究的二元关系，都是齐次二元关系。

性质

研究二元运算时，我们常常关注以下这些特殊的性质

1. 自反性（reflexive）：\((\forall~a \in S)~~aRa\)，
2. 反自反性（irreflexive，anti-reflexive）：\((\forall~a \in S)~~\lnot(aRa)\)，
3. 对称性（symmetric）：\((\forall~a,b \in S)~~aRb \iff bRa\)，
4. 反对称性（antisymmetric）：\((\forall~a,b \in S)~~(aRb \land bRa) \implies a=b\)，
5. 传递性（transitive）：\((\forall~a,b,c \in S)~~(aRb \land bRc) \implies aRc\)，
6. 连接性（connected）：\((\forall~a,b \in S)~~a \neq b \implies (aRb \lor bRa)\)
   （若 \(aRb \lor bRa\)，则称 \(a\) 和 \(b\) 可比的），
7. 不可比的传递性（transitive of incomparability）：\((\forall~a,b,c \in S)~~(\lnot(aRb \lor bRa) \land \lnot(bRc \lor cRb)) \implies \lnot(aRc \lor cRa)\)
   （若 \(\lnot(aRb \lor bRa)\)，则称 \(a\) 和 \(b\) 是不可比的）。

试着确定 \(=~\neq~\lt~\le~\subseteq~\mid~\) 等常见的二元关系满足哪些性质。

分类

根据各种二元关系所具有的性质，我们可以对二元关系进行分类，最常见的是偏序（partial order）和全序（total order）。

\(\S\) 偏序（partial order）：满足自反性、反对称性和传递性的二元关系，即：

• \((\forall~a \in S)~~aRa\)
• \((\forall~a,b \in S)~~(aRb \land bRa) \implies a=b\)
• \((\forall~a,b,c \in S)~~(aRb \land bRc) \implies aRc\)

其对应的定义域被称为偏序集。

\(\S\) 全序（total order）：满足自反性、反对称性、传递性和连接性的二元关系，即：

• \((\forall~a \in S)~~aRa\)
• \((\forall~a,b \in S)~~(aRb \land bRa) \implies a=b\)
• \((\forall~a,b,c \in S)~~(aRb \land bRc) \implies aRc\)
• \((\forall~a,b \in S)~~a \neq b \implies (aRb \lor bRa)\)

其对应的定义域被称为全序集，全序是一种特殊的偏序。

举个例子？定义域 \(\{1,2,4,6\}\) 上的二元关系 \(\mid\) 是一个偏序，显然它满足 自反性、反对称性和传递性，但它并非一个全序，因为不满足连接性，\(4\) 和 \(6\) 是不可比的。

当然，你可以通过改变定义域使得它成为一个全序：将定义域改成 \(\{1,2,4,8\}\)，在这个特定的定义域下，任意两个元素可比，满足连接性，因此此时 \(mid\) 变成了一个全序。

偏序集

下面我们将研究偏序集的一些性质。

偏序集的可视化表示：Hasse 图

我们可以用 Hasse 图来表示有限偏序集上的偏序关系。

\(\S\) Hasse 图：对有限偏序集 \(S\) 和其上的偏序 \(\preceq\)，定义 \(x\prec y\iff (x\preceq y\land x\neq y)\)，其对应的 Hasse 图为满足如下条件的（有向）图 \(G=\langle V,E\rangle\)：

• \(V=S\),
• \(E=\{(x,y)\in \text{id}_S: x\prec y \land ((\nexists~z\in S)~~x\prec z\prec y)\}\)

\(p.s.\text{ id}_S = \{(x,x):x\in S\}\)

比如说，以 \(\{1,2,3\}\) 的幂集——即其所有子集构成的集合为偏序集的偏序 \(\subseteq\) 所对应的 Hasee 图：

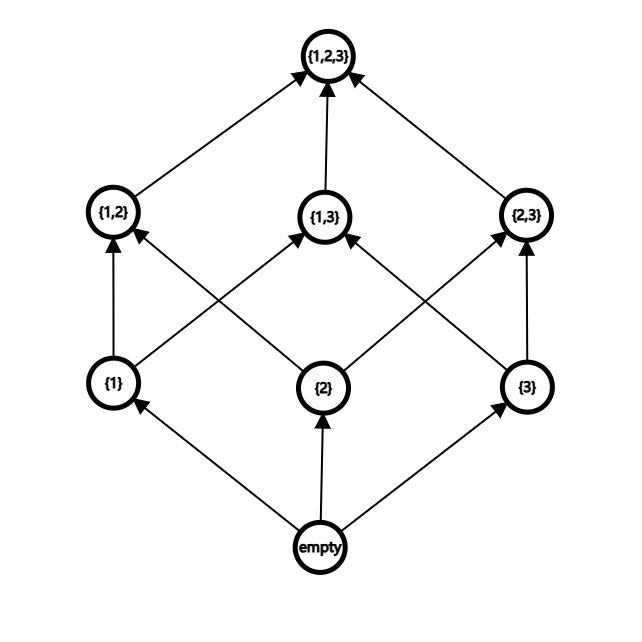
\(\S\) 定理：Hasse 图一定是一个 DAG。

这个结论看起来很简单，但你可以试着证明一下，就当作是练习和巩固前面的这一坨定义。

\(\S\) 引理：对偏序集 \(S\) 和其上的偏序 \(\preceq\)，定义 \(x\prec y\iff (x\preceq y\land x\neq y)\)，\(\prec\) 具有传递性即 \((\forall~a,b,c \in S)~~a\prec b\land b\prec c \implies a\prec c\)。

引理证明：
\(\because~a\prec b\land b\prec c\)
\(\therefore~a\preceq b\land b\preceq c\land a\neq b\land b\neq c\)
\(\therefore~a\preceq c\land a\neq b\land b\neq c\)
显然当 \(a\neq c\) 时，有 \(a\prec c\)，接下来说明不可能有 \(a=c\)。
反证法，假设 \(a=c\)，
\(\because~a\preceq b\land b\preceq c\)
\(\therefore~a\preceq b\land b\preceq a\)
\(\therefore~a=b\)
此时 \(a=b\) 与 \(a\neq b\) 矛盾，所以不可能有 \(a=c\)。
于是有 \((\forall~a,b,c \in S)~~a\prec b\land b\prec c \implies a\prec c\)。
引理得证。

接着就可以证明 Hasse 图是个 DAG 了。

定理证明：

有向性显然，接下来证明无环性。

反证法，假设存在一个环，环上元素为 \(a_1,a_2,a_3,\cdots,a_n\)，那么有：
\(a_1\prec a_2\prec a_3\prec\cdots a_m\prec a_1\)

由引理可知 \(a_1\prec a_1\) 即 \(a_1\prec a_1\land a_1\neq a_1\)，
此时矛盾，于是不存在环，无环成立，Hasse 图是一个 DAG。
\(\mathcal{Q.E.D.}\)

链与反链

\(\S\) 链（chain）：偏序集 \(S\) 和其上的偏序 \(\preceq\)，称 \(S\) 的全序子集为 链。

\(\S\) 反链（antichain）：若 \(S\) 的子集 \(T\) 中任意两个不同元素均不可比（即 \((\forall~a,b \in T)~~a \neq b \implies (a \npreceq b \land b \npreceq a)\)），则称 \(T\) 为 反链。

对偏序集 \(S\) 和其上的偏序 \(\preceq\)，我们将偏序集 \(S\) 的最长反链长度称为 宽度（partial order width）。

由于全序集比偏序集更严格的地方体现在全序集满足连接性，即任意两元素可比，所以我们可以这么表述：

偏序集 \(S\) 的链是其上的一子集，并且满足任意两元素可比。
偏序集 \(S\) 的反链是其上的一子集，并且满足任意两元素不可比。

比如说，对于前面提到过的偏序集 \(\{1,2,4,6\}\) 及其上的偏序 \(\mid\)，\(\{1,2,4\}\) 是一条合法的链，因为 \(\{1,2,4\}\) 中任意两个元素可比，满足连接性，是一个全序子集；而其中的 \(\{4,6\}\) 则是一条反链，因为其中任意两个元素不可比。

再举个例子，\(\{1,2,3\}\) 的幂集形成的偏序集及其上的偏序 \(\subseteq\) 中，\(\{\varnothing,\{1\},\{1,2\},\{1,2,3\}\}\) 为一条链，\(\{\{1\},\{2,3\}\}\) 为一条反链，其宽度为 \(3\)，比如说反链 \(\{\{1\},\{2\},\{3\}\}\) 即为一个合法的长为 \(3\) 的反链，可以证明不存在更长的反链。

链与反链在 Hasse 图的意义

我们来研究链与反链在 Hasse 图上的意义。

以 \(\{1,2,3\}\) 的幂集形成的偏序集及其上的偏序 \(\subseteq\) 为例，建出其对应的 Hasse 图。

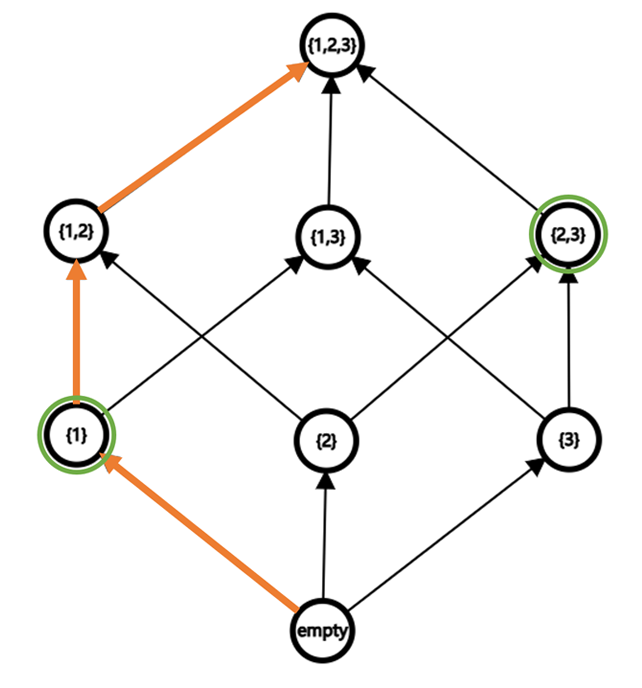
这里标注的橙色连接的是链 \(\{\varnothing,\{1\},\{1,2\},\{1,2,3\}\}\)，绿色则是反链 \(\{\{1\},\{2,3\}\}\) 的元素。

发现规律了吗？

一条链对应着 Hasse 图上的一条路径，一条反链上任意两不同元素之间互不可达。

原因也很好解释：

链上元素两两可比，所以必然上在 Hasse 图上任意两元素间由路径连接，又因为 Hasse 图上是个 DAG，所以链上元素必然在同一路径上。

反链上元素两两不可比，所以其元素在 Hasse 图上两两之间互不存在路径，即两两互不可达。

Dilworth 定理与 Mirsky 定理

Dilworth 定理和 Mirsky 定理是（有限）偏序集上的重要定理，是序理论的重要内容，在 OI 中有诸多应用。

Dilworth 定理

\(\S\) Dilworth 定理（Dilworth Theorem）：对有限偏序集 \(S\) 及其上的偏序 \(\preceq\)，\(S\) 的宽度（最小反链长度）等于最小链划分。

最小链划分，即可以将原偏序集划分为最少多少条链。

证明：

设偏序集 \(S\) 的宽度（最长反链长度）为 \(m\)，最小链划分为 \(n\)。

由于反链内元素两两不可比，于是一条反链内 \(m\) 个元素必然被划分到 \(m\) 个不同的链中，所以显然有 \(n\ge m\)。

接下来考虑在 Hasse 图上进行分析。

使用数学归纳法，

基本情形 \(\lvert S\rvert=1\) 下，显然有 \(n=m=1\)，满足 Dilworth 定理。

接下来假设 \(\lvert S \rvert=x-1\) 时 Dilworth 定理成立，那只需证明 \(\lvert S \rvert=x\) 时也成立即可。

由于 Hasse 图是个 DAG，由图论基本知识，必然存在一个无入度的点。

我们考虑除去这个点及与它有关的所有边，得到一个有 \(x-1\) 个结点的新 Hasse 图，于是满足 Dilworth 定理，设这个新 Hasse 图的宽度和最小链划分为 \(k\)，其中有 \(t\) 条最长反链（长度为 \(k\)），再设最小链划分的一合法方案为 \(\{S_1,S_2,S_3,\cdots,S_k\}\)，\(t\) 条最长反链分别为 \(\{T_1,T_2,T_3,\cdots,T_t\}\)。

由于反链内元素两两不可比，所以 \(T_i\) 的 \(k\) 个元素一定来源于 \(k\) 条不同的链上，又因为最小链划分只有 \(k\) 条，于是有 \(T_i=\{a_1,a_2,a_3,\cdots,a_k\}\)，其中 \(a_i\in S_i\)。

接下来设 \(A_i\) 为反链 \(T_1\) 至 \(T_t\) 这 \(t\) 条反链在 \(S_i\) 中选走的最大元素。

这里先证明一个引理：\(\{A_1,A_2,A_3,\cdots,A_k\}\) 是一条反链。

证明：反证法，假设 \((\exist~ i,j)~~A_i\preceq A_j\lor A_j\preceq A_i~(i\neq j)\)，不失一般性，设有 \(A_i\preceq A_j\)。

那么选择了 \(A_j\) 的那条最长反链 \(T_x\) 在 \(S_i\) 中就不能选择 \(A_i\) 了，不然就会出现 \(A_i\) 与 \(A_j\) 可比，又由于 \(A_i\) 是 \(S_i\) 中被最长反链所选择的最大元素，于是 \(T_x\) 就只能在 \(S_i\) 中选择一个比 \(A_i\) 小的元素 \(p\preceq A_i\)。（实际上这里可以用更严格的 \(\prec\)，即 \(p\prec A_i\)）

此时，因为 \(A_i\preceq A_j\land p\preceq A_i\)，由偏序关系的传递性知 \(p\preceq A_j\)，那么 \(p\) 和 \(A_j\) 就可比了，所以不能把 \(p\) 选进 \(T_x\)。

那么就相当于 \(T_x\) 不能选 \(S_i\) 中的任一元素了，与前文中 “于是有 \(T_i=\{a_1,a_2,a_3,\cdots,a_k\}\)，其中 \(a_i\in S_i\)” 矛盾，假设不成立，不存在可比的两个不同的 \(A\) 的值，于是 \(\{A_1,A_2,A_3,\cdots,A_k\}\) 是一条反链。

引理得证。

OK，现在我们把原来扔掉了的那个无入度点放回 Hasse 图中，如果设现在这个 Hasse 图的的宽度（最长反链长度）为 \(m\)，最小链划分为 \(n\)，那么显然有 \(m=k\lor m= k+1\) 和 \(n=k\lor n=k+1\)，因为这个无入度的点至多使宽度和最小链划分增加 \(1\)。

先设这个无入度的点对应 \(S\) 中的元素 \(e\)，接下来分类讨论。

\(Case~1.~~(\forall~i)~~\neg(A_i\preceq e\lor e\preceq A_i)\)，即所有 \(A_i\) 与 \(e\) 不可比。

由引理， \(\{A_1,A_2,A_3,\cdots,A_k\}\) 是一条反链，又因为所有 \(A_i\) 与 \(e\) 不可比，所以 \(\{A_1,A_2,A_3,\cdots,A_k,e\}\) 是一条反链，其长度为 \(k+1\)，又因为最长反链长度 \(m\) 满足 \(m=k\lor m= k+1\)，所以 \(m=k+1\)。

又因为 \(n\ge m\) 且 \(n=k\lor n=k+1\)，所以 \(n=m=k+1\)。

\(Case~2.~~(\exist~i)~~A_i\preceq e\lor e\preceq A_i\)，即存在 \(A_i\) 与 \(e\) 可比。

那么显然 \(e\) 可以归到链 \(S_i\) 里去，因为 \(e\) 对应了一个无入度的点，所以它必然是这条链中的最小元，所以最小链覆盖 \(n=k\)，让 \(S_i\) 并上 \(\{e\}\) 即可。

又因为 \(n\ge m\) 且 \(m=k\lor m= k+1\)，所以 \(n=m=k\)。

综上，\(n=m\)。

归纳性地，对有限偏序集 \(S\) 及其上的偏序 \(\preceq\)，\(S\) 的宽度（最小反链长度）等于最小链划分。

\(\mathcal{Q.E.D.}\)