轻重链剖分

性质

重链

重链内编号连续，可以用线段树维护一些值

路径

对于树上任意两点\(x,y\)，它们的路径经过的重链不超过\(logn\)条

树剖正是运用这种方式，把1个修改/询问变成\(logn\)个修改/询问，然后高效求解

注意：树剖的作用是将树上问题拆成\(logn\)个序列问题，并不是所有树剖都一定要用线段树，只要能对序列问题进行高效维护就行了

子树

子树内编号连续（其实任意子树的\(dfn[]\)都是连续的），对于子树内统计求和可以用线段树实现

注意这里只是用了树剖的编号思想，实际做题不一定用得到

细节实现

跳链时深度判断：dep[top[x]]<dep[top[y]]

如在路径加权时：

void Line_plus(int x,int y,int k) {
	while(top[x]!=top[y]) {
		if(dep[top[x]]<dep[top[y]]) swap(x,y);
		Plus(1,1,n,k,num[top[x]],num[x]);
		x=fa[top[x]];
	}
	if(dep[x]>dep[y]) swap(x,y);
	Plus(1,1,n,k,num[x],num[y]);
}

如果第三行的dep[top[x]]<dep[top[y]]写成了dep[x]<dep[y]，就会导致x会跳到0，导致线段树死循环（L,R其中一个为0）

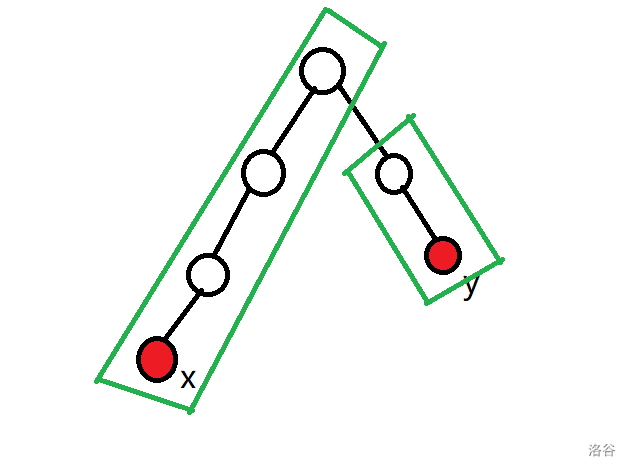
如图，dep[x]>dep[y]如果x先跳，会使x直接跳出树

P4211 [LNOI2014]LCA

模型：\(\sum_{i=1}^ndep(LCA(i,x))\)

考虑改变\(dep(LCA(x,y))\)的意义：\(LCA(x,y)\)走到根节点所经过的点的数量

如果我们对\(y\)走到根节点经过的点染色，那么\(x\)走到根节点经过的有颜色的点的数量，刚好为\(LCA(x,y)\)走到根节点所经过的点的数量

计算多点与\(x\)的\(LCA\)时，我们考虑多点同时“染色”，再让\(x\)“走”到根节点，即每个点对到根节点的路径权值加\(1\)，再统计\(x\)到根的路径权值和

P5305 [GXOI/GZOI2019]旧词

前一题的加强版（但是完全没加强（但是我没想到（看题解又看了半天才理解，我是sb）））

即用线段树维护：

1、区间\([l,r]\)每个数加上\(dep_i^k-(dep_i-1)^k\)

2、查询区间\([l,r]\)的数的和

题解中说的预处理区间权值和的区间其实是线段树的结点\(x\)控制的区间\([l,r]\)，即区间\([l,r]\)全被打标记时直接用预处理的数更新\(sum[]\)，然后上传

写这段解释时更加感觉没想出来的我是sb