树链剖分

重链剖分

【问题引入】

问题描述

给定一颗有 $n$ 个节点、带边权的树，现在有对树进行 $m$ 个操作，操作有 $2$ 类：

• 将节点 $a$ 到节点 $b$ 路径上所有边权的值都改为 $c$；
• 询问节点 $a$ 到节点 $b$ 路径上的最大边权值。

请你写一个程序依次完成这 $m$ 个操作。

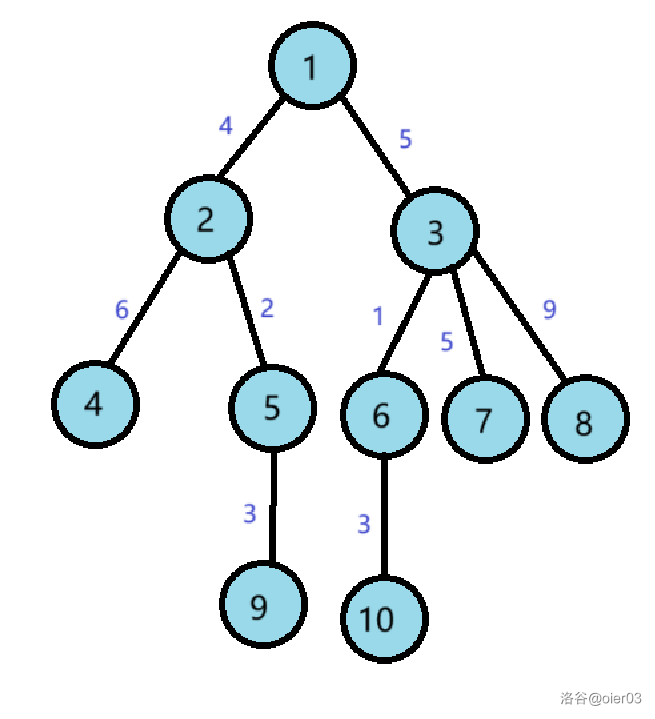
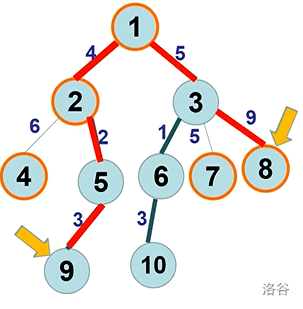
有三个操作

• 修改 $2$ 号到 $9$ 号节点路径上的边值为 $7$；

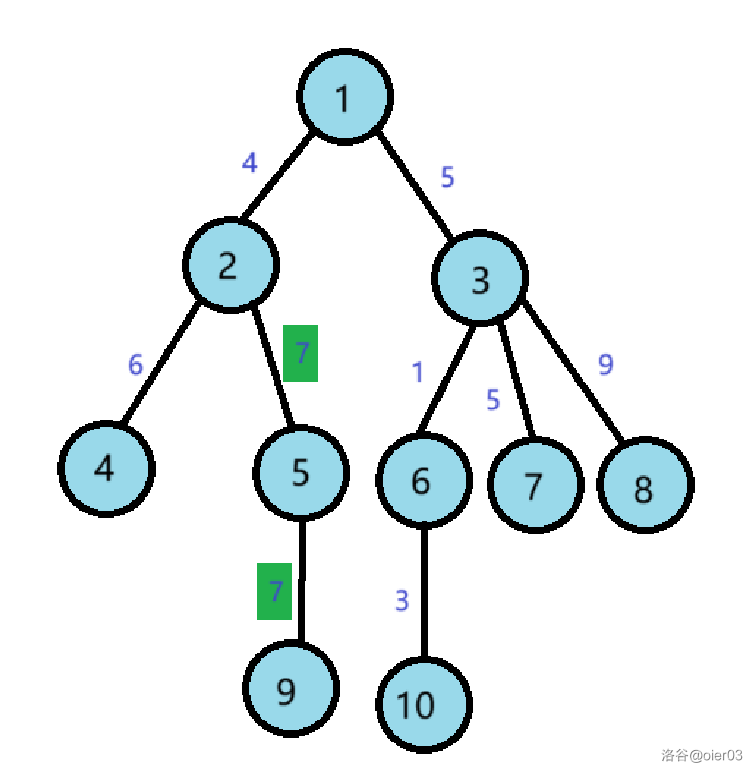
• 修改 $2$ 号到 $7$ 号节点路径上的边值为 $4$ ；

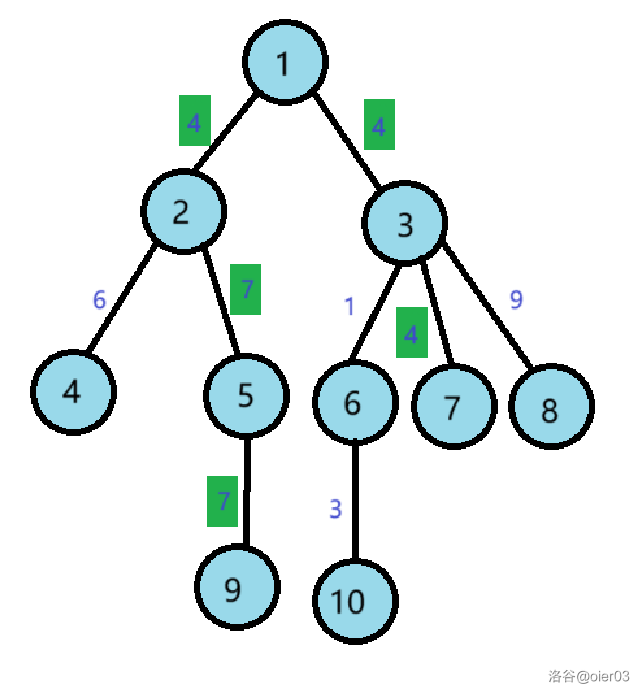
• 查询 $9$ 号到 $8$ 号节点路径上的最大边权值。

每次修改和查询复杂度为 $O(n)$。

$\color{red}思考：既然每个操作都与树上的路径有关，能否把这些路径分段存储，方便修改和查询？$

【树链剖分的概念】

树链剖分是指一种对树进行划分的算法，它先通过轻重边剖分 $(Heavy-Light\ Decomposition)$ 将树分为多条链，保证每个点属于且只属于其中一条链，然后再通过数据结构（树状数组、SBT、SPLAY、线段树等）来维护每一条链。

使用这种方法后，一般可以将修改和查询的复杂度降为 $O(log_2\ n)$。

【树链剖分的方法】

定义

将树中的边分为：重边和轻边。

定义 $size(X)$ 为以 $X$ 为根的子树的节点个数。

令 $V$ 为 $U$ 的儿子节点中 $size$ 值最大的节点，那么 $V$ 称为 $U$ 的$\color{red}重儿子$，边 $(U,V)$ 被称为$\color{red}重边$，树中重边之外的边被称为$\color{red}轻边$，全部由重边构成的路径称为$\color{red}重链$。

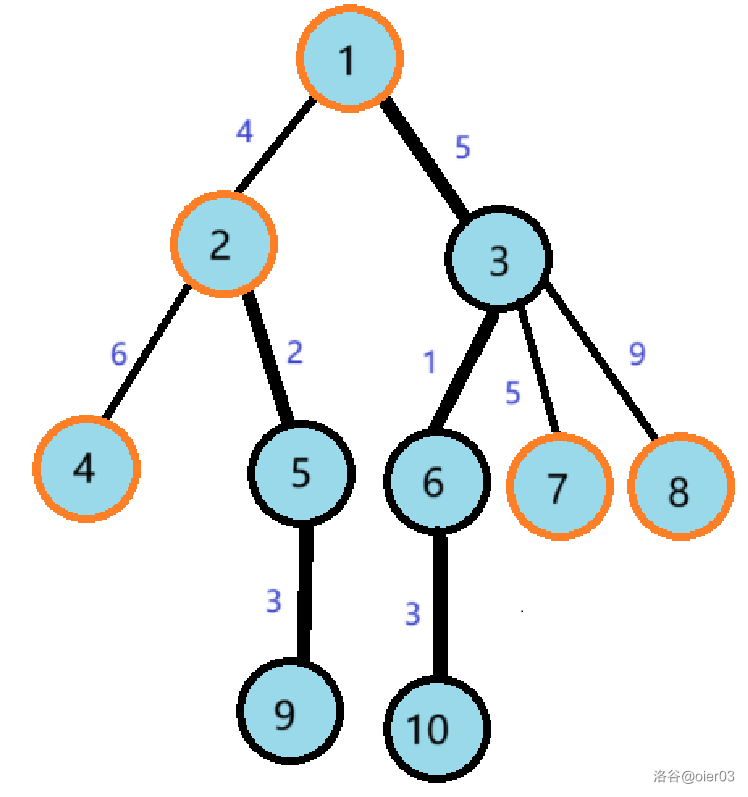
性质1

对于轻边 $(U,V)$，$size(V)\le size(U)\div 2$。

从根到某一点的路径上，不超过 $log_2 N$ 条轻边，不超过 $log_2 N$ 条重路径。

特例

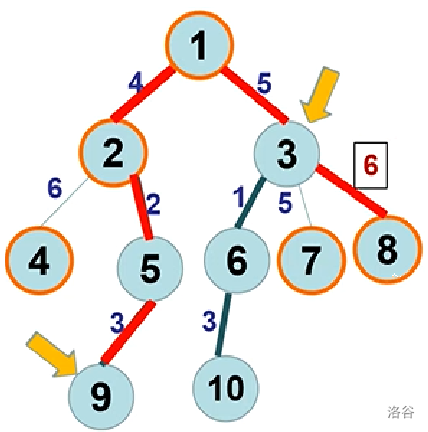
图中有 $5$ 条重链：

• $1\to 3\to 6\to 10$
• $2\to 5\to 9$
• $4$
• $7$
• $8$

性质2

每一条链首深度大于 $1$ 的重链都可以通过其$\color{red}链首的父亲节点$连到$\color{red}另一条重链$上。

核心定义

$size[i]$：以节点 $i$ 为根的子树中节点的个数；

$son[i]$：节点 $i$ 的重儿子；

$dep[i]$：节点 $i$ 的深度，根的深度为 $1$；

$top[i]$：节点 $i$ 所在重链的链首节点；

$fa[i]$：节点 $i$ 的父节点；

$tid[i]$：在 DFS 找重链的过程中为节点 $i$ 重新编的号码，每条重链上的编号节点是连续的。

两次DFS

• 第一次DFS：找重边，顺便求出所有的 $size[i],dep[i],fa[i],son[i]$；
• 第二次DFS：将重边连成重链，顺便求出所有的 $top[i],tid[i]$。

第一次DFS

找重边，顺便求出所有的 $size[i],dep[i],fa[i],son[i]$；

第二次DFS

将重边连成重链，顺便求出所有的 $top[i],tid[i]$。

从根节点开始 ，沿重边向下扩展，连成重链；

不能加入当前重链上的节点，以该节点为链首向下拉一条新的重链（如果该节点是叶子节点，则自己构成一条重链）；

DFS 过程中，对节点重新编号，因为是沿重边向下扩展，故一条重链上的节点新编号会是连续的。

参考代码

void DFS_2(int u, int sp) {//第二遍dfs求出top[],p[],fp[]的值
    top[u] = sp;
    p[u] = pos++;
    fp[p[u]] = u;
    if (son[u] != -1) DFS_2(son[u], sp);//先处理重边
    for (int i = head[u]; i != -1; i = edge[i].next) {//再处理轻边情况
        int v = edge[i].to;
        if (v != son[u] && v != prt[u])
            DFS_2(v, v);//轻链的顶点就是自己
    }
}

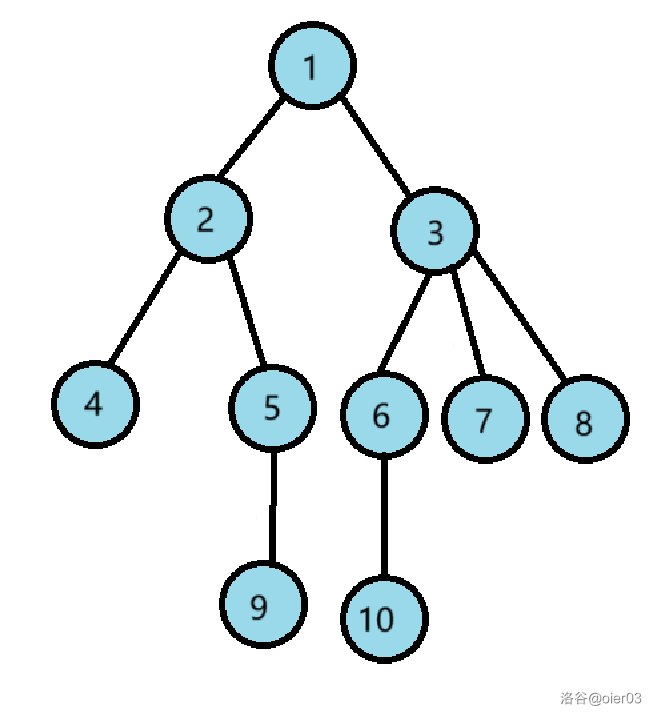
【树链剖分的过程】

重链剖分后

剖分完成后，每条重链相当于一段区间，将所有的重链收尾相接，用适合的数据结构来维护这个整体。

• $tid[i]$：$\color{red}节点\ i$ 所对应的新编号
• $rank[i]$：$\color{red}编号\ i$ 所在原树中对应的节点编号

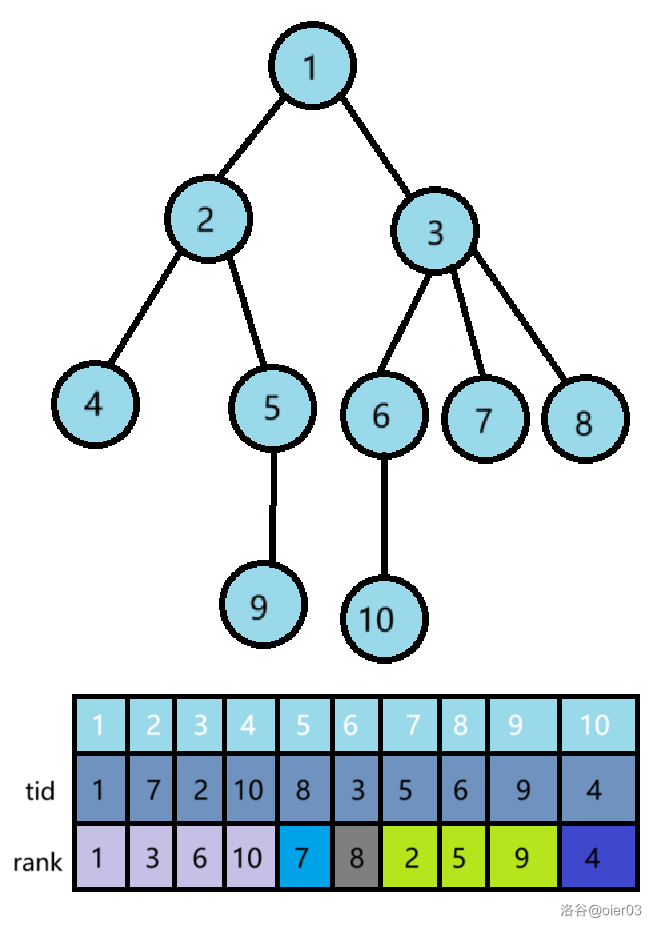
我们可以采用 $\Large\color{red}线段树$等数据结构维护每条重链。

以线段树维护为例

维护节点 $u,v$ 路径上的最大值

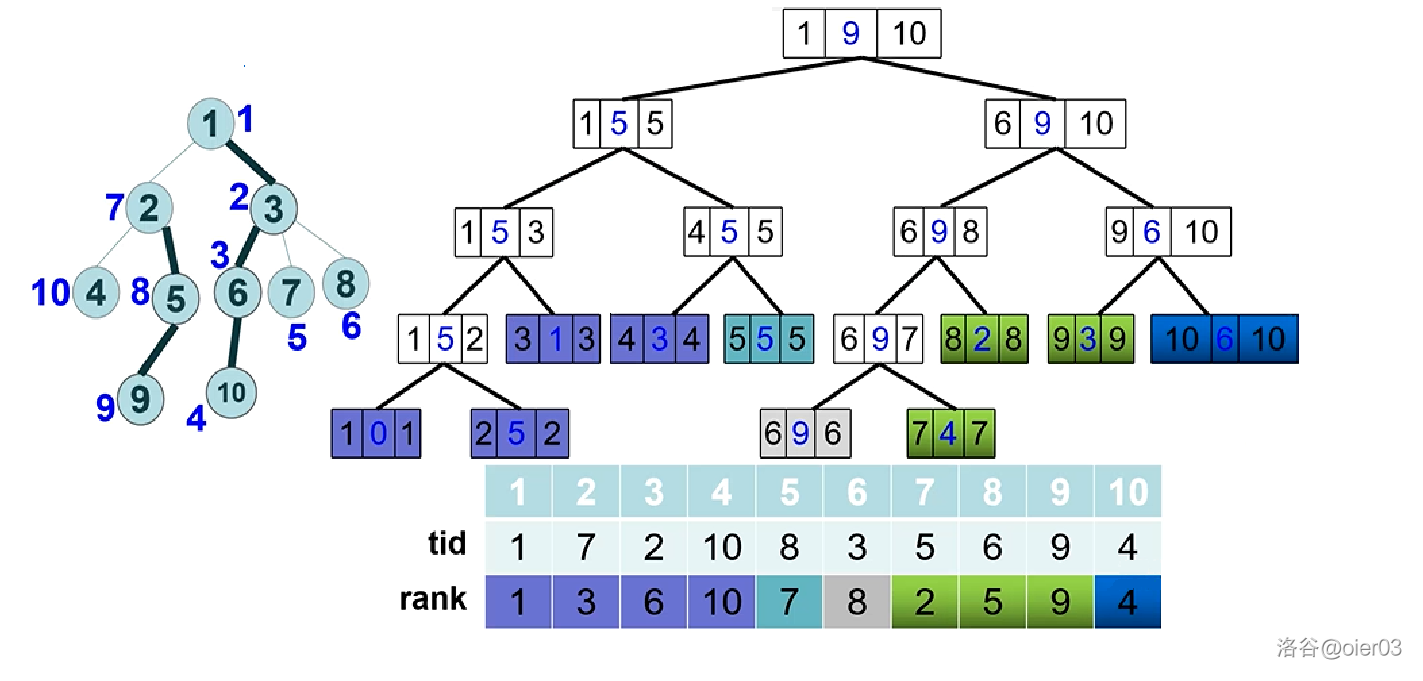
【树链剖分的修改操作】

即整体修改点 $U$ 和点 $V$ 的路径上每条边的权值。

点 $U$ 和点 $V$ 的关系分为两种情况：

• 情况 $1$ ：$U$ 和 $V$ 在同一条重链上；
• 情况 $2$ ：$U$ 和 $V$ 不在同一条重链上。

情况 $1$

以修改边为例：将原树中的边（$6\to 10$）权值修改为 $6$（$\color{red}边的权值存在边所到达顶点中$）。

$10$ 号节点的新编号为 $4$，故只需修改线段树中的 $[4,4]$ 的值即可。

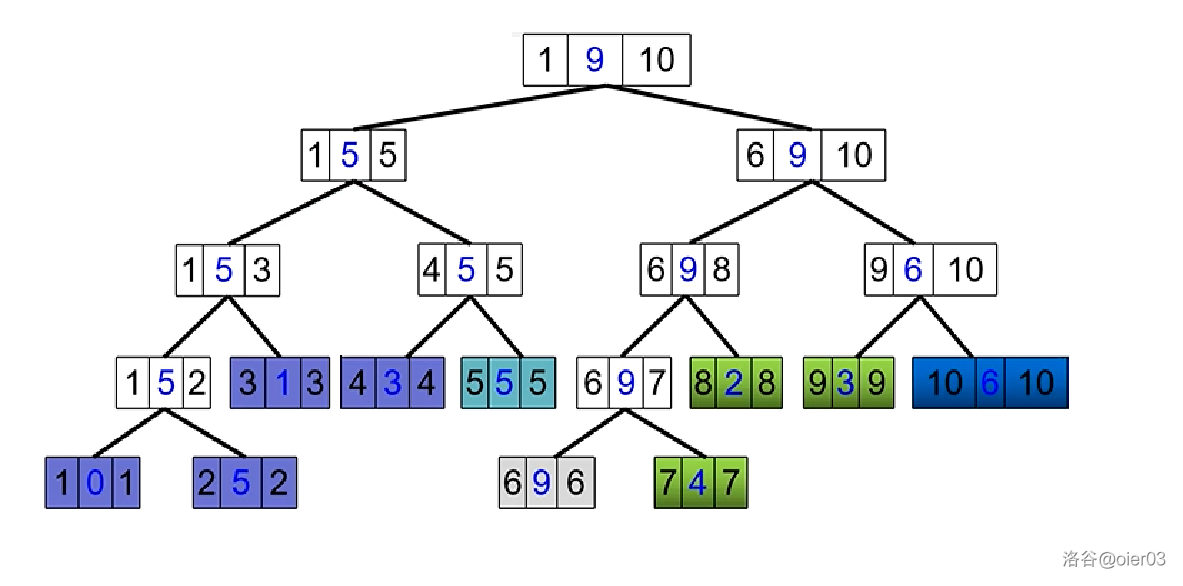
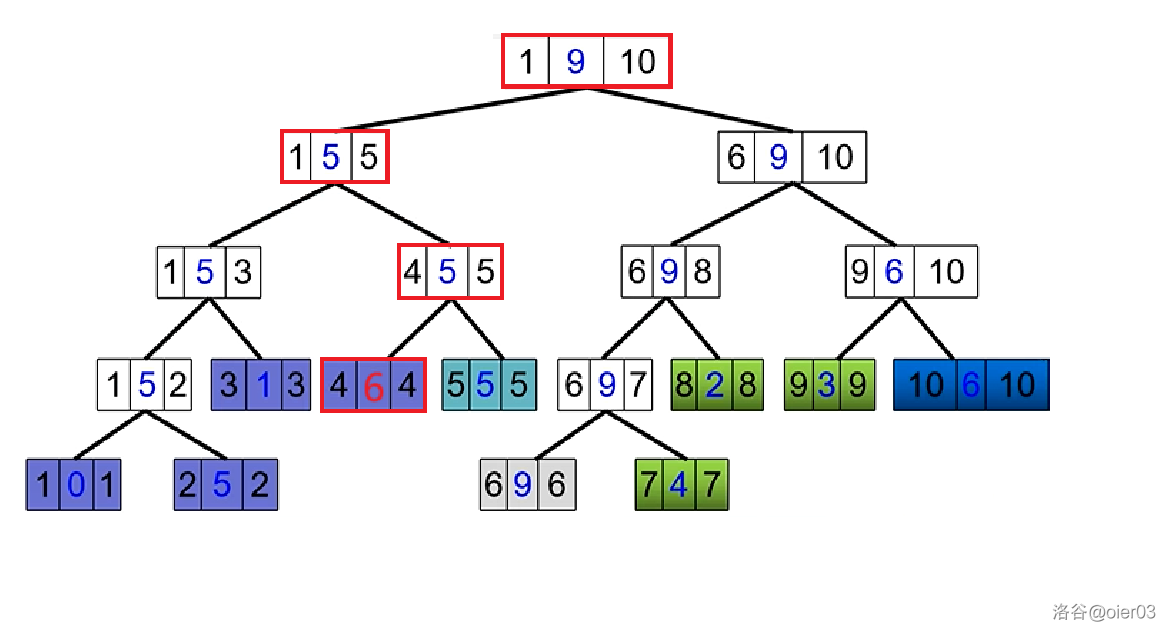
$2$ 号和 $9$ 号节点的新编号分别为 $7$ 和 $9$，需要修改的区间为 $tid[son[2]]\sim tid[9]$，即 $[8,9]$。

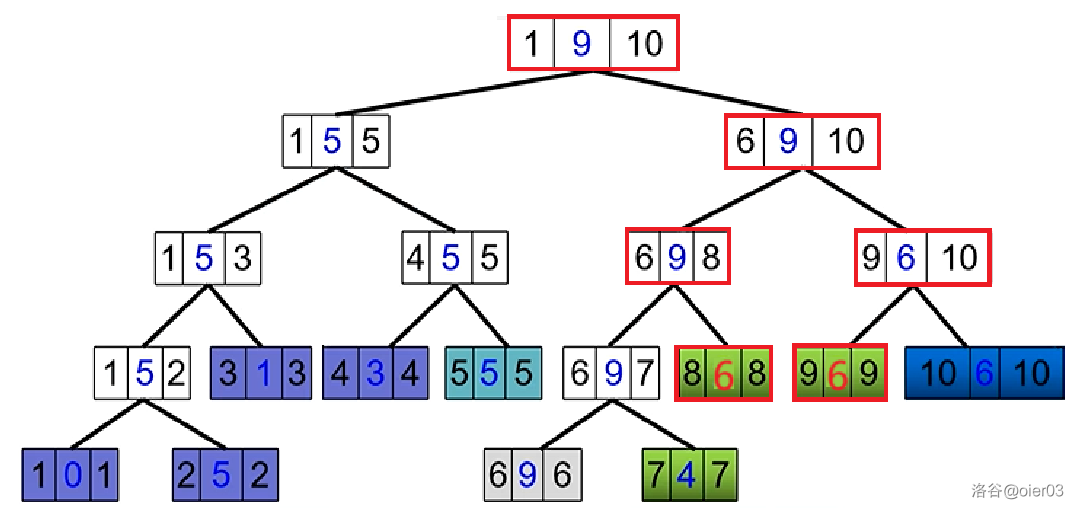
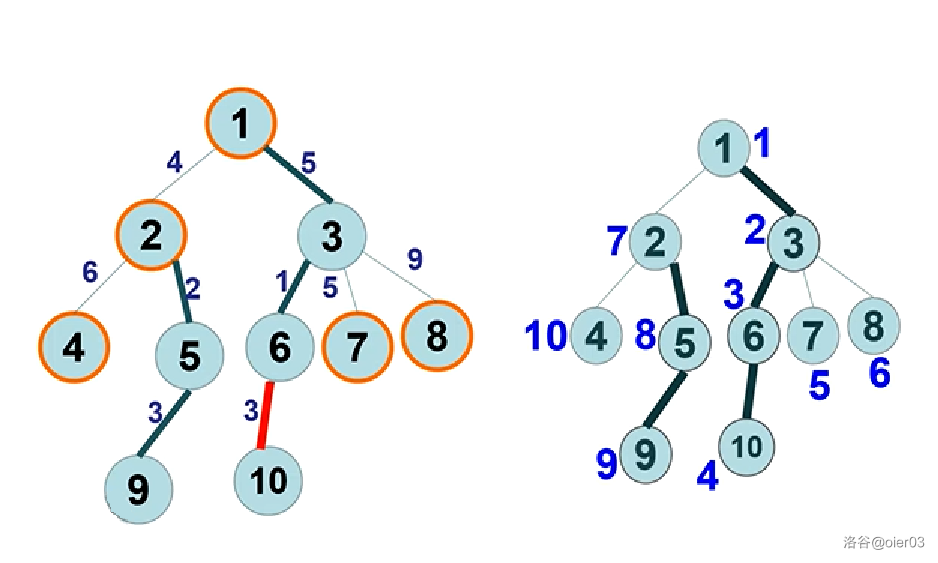
情况 $2$

将原树中路径 （$8\to 9$）上所有边的权值都修改为 $8,\ top[9]=2,\ top[8]=8$。

它们不在同一条重链上，需要分段修改，边修改边$\color{red}往一条重链上靠$。

优先将$\color{red}链首$深度大的点往上爬，向另一条重链靠，直到两者爬到同一条重链，转换为情况 $1$ 解决。

后面的图不画了。

【树链剖分的查询操作】

和修改操作类似。

设查询 $u\to v\ \max$。

情况 $1$

$top[u] = top[v]$

在线段树上查询 $u\sim v$ 的区间即可。

情况 $2$

$top[u]\ne top[v]$

向上爬树，深度大的优先，深度一样随便爬一个。

重复这个操作，直到 $top[u] = top[v]$，转换成情况 $1$ 处理。

参考代码

int Change(int u, int v) {//查询 u -> v 边的最大值
    int f1 = top[u], f2 = top[v];
    int tmp = 0;
    while (f1 != f2) {
//u 和 v 不在同一条重路径，深度深的点向上爬，直到在同一条重（轻）路径上为止
        if (dep[f1] < dep[f2]) {
            swap(f1, f2);
            swap(u, v);
        }
        tmp = max(tmp, Query(1, p[f1], p[f2]));
        //在重链中求 u 和链首端点 f1 路径上的最大值
        u = prt[f1];
        f1 = top[u];
    }
    if (u == v) return tmp;//为同一点，则退出
    if (dep[u] > dep[v])
        swap(u, v);
    return max(tmp, Query(1, p[son[u]], p[v]));
}
//Query(v, l, r) 查询线段树中 [l,r] 的最大值

实链剖分

没有

长链剖分

没有