格林公式7

标签：格林 frac int Big text 公式 partial aligned

例1 计算积分

\[I=\int_Cx^2ydx-xy^2dy, \]

其中C是上半圆 \(\begin{aligned} & \text{ }x^2+y^2=a^2,y\geqslant0,\text{ }\\ & \end{aligned}\) 逆时间方向

\[\begin{aligned} & \text{ }x^2+y^2=a^2,y\geqslant0,\text{ }\\ & \end{aligned} \]

考虑到上半圆的边界，他由C以及\((x,0) \quad (x\in [-a,a])\) 组成，在上半圆用Green公式，得

\[I=\int_{\{x^2+y^2\leqslant a^2, y\geqslant0\}}(-x^2-y^2)dxdy=-\int_0^\pi d\theta\int_0^ar^3dr=-\frac{\pi}{4}a^4. \]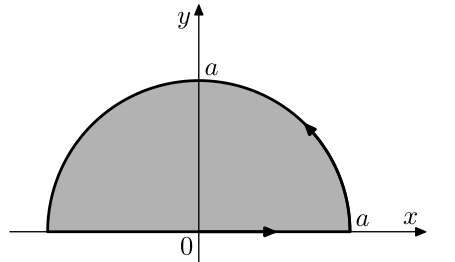

例2 计算积分

设 Ω 为包含原点的有界区域 , 其边界为 C 1 曲线 , 方向为诱导定向 . 计算积分

\[\begin{aligned}I=\int_{\partial\Omega}\frac{-ydx}{x^2+y^2}+\frac{xdy}{x^2+y^2}.\end{aligned} \]

取中心为原点的小圆 \(x^2 + y^2 = \varepsilon^2\) , 使得 $B_{\varepsilon}(0)\subset\Omega \(. 小圆上的定向规定为逆时针方向 ( 从而与诱导定向相反 ), 在区域\)B_{\varepsilon}(0)\subset\Omega $中利用 Green 公式 , 得

\[\begin{aligned} \text{I}& =\int_{x^2+y^2=\varepsilon^2}\left(\frac{-ydx}{x^2+y^2}+\frac{xdy}{x^2+y^2}\right) \\ &+\int_{\Omega-B_{\varepsilon}(0)}\Big[\frac{\partial}{\partial x}\Big(\frac{x}{x^{2}+y^{2}}\Big)+\frac{\partial}{\partial y}\Big(\frac{y}{x^{2}+y^{2}}\Big)\Big]dxdy \\ &=\int_0^{2\pi}d\theta=2\pi. \end{aligned} \]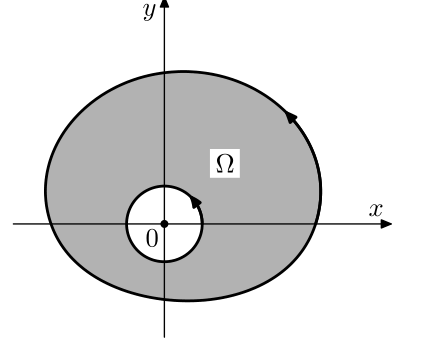

标签：格林,frac,int,Big,text,公式,partial,aligned
From： https://www.cnblogs.com/redufa/p/18424635