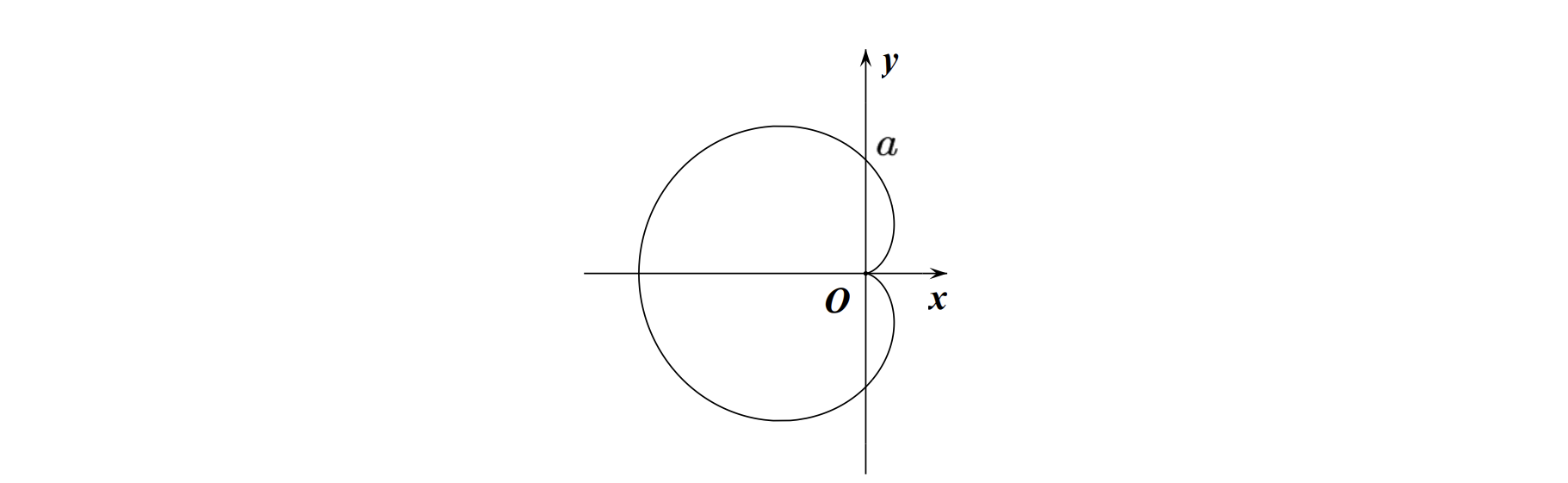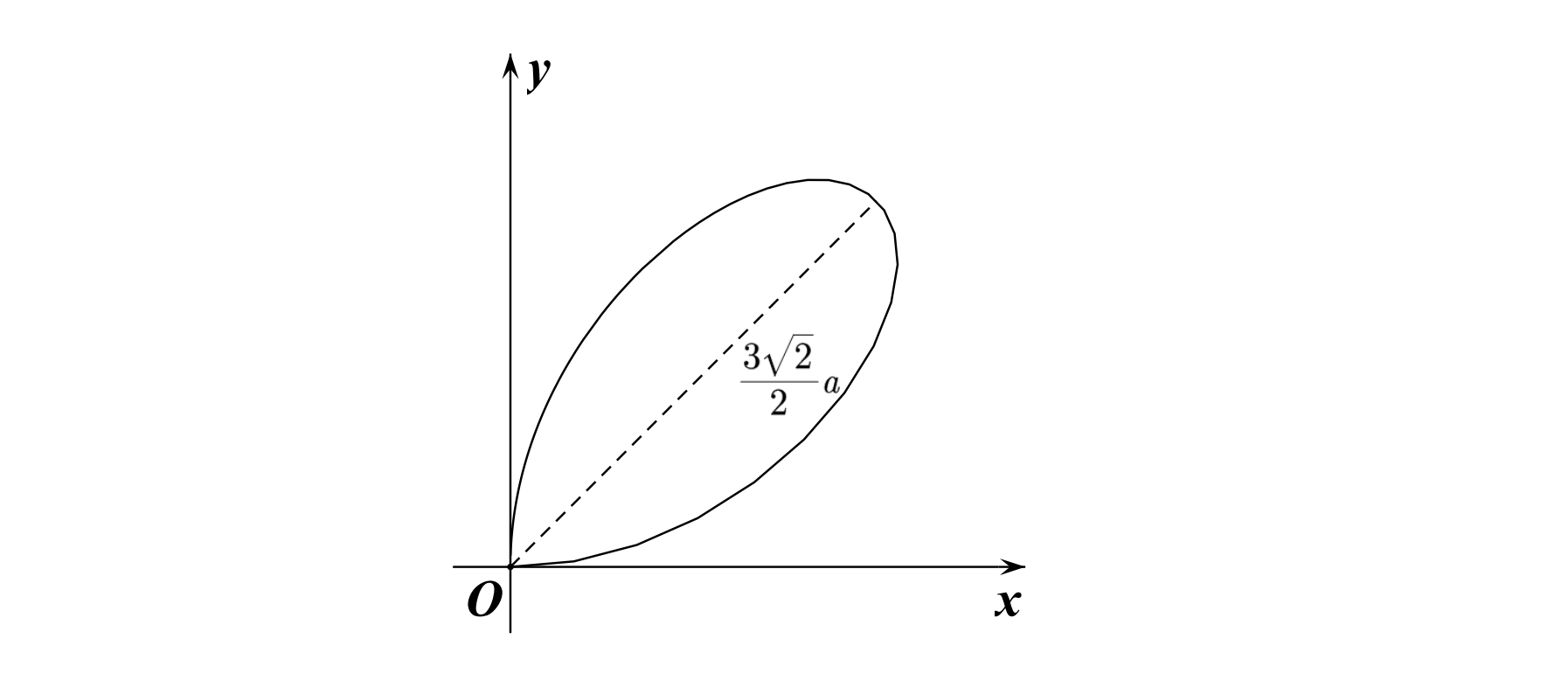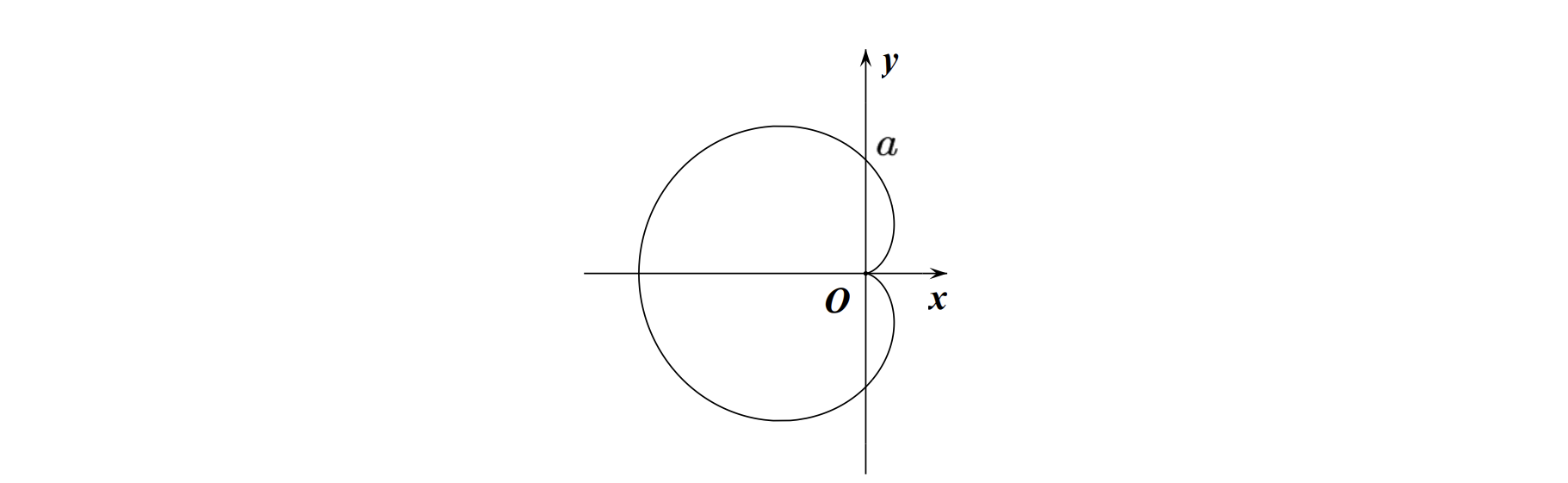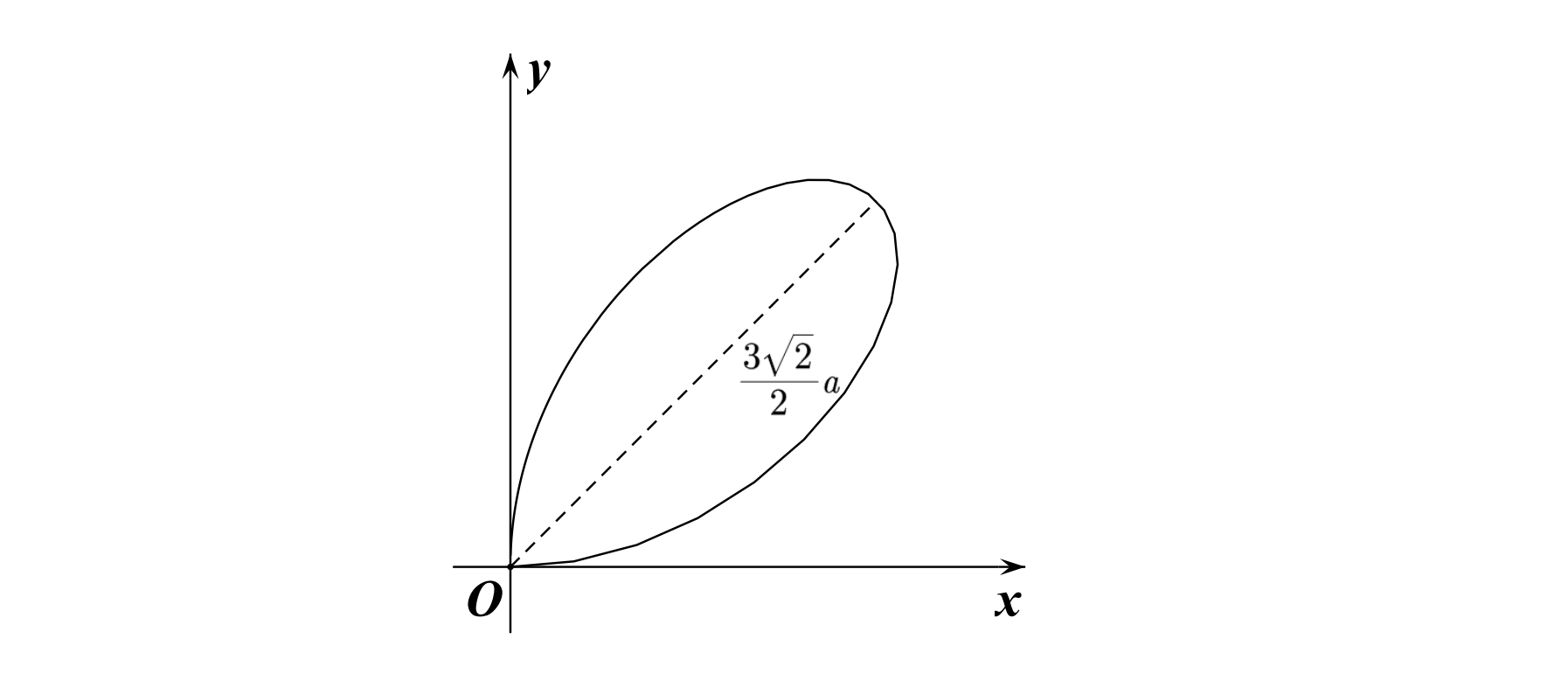标签:right text 曲线 rho theta array 高等数学 极坐标 考研
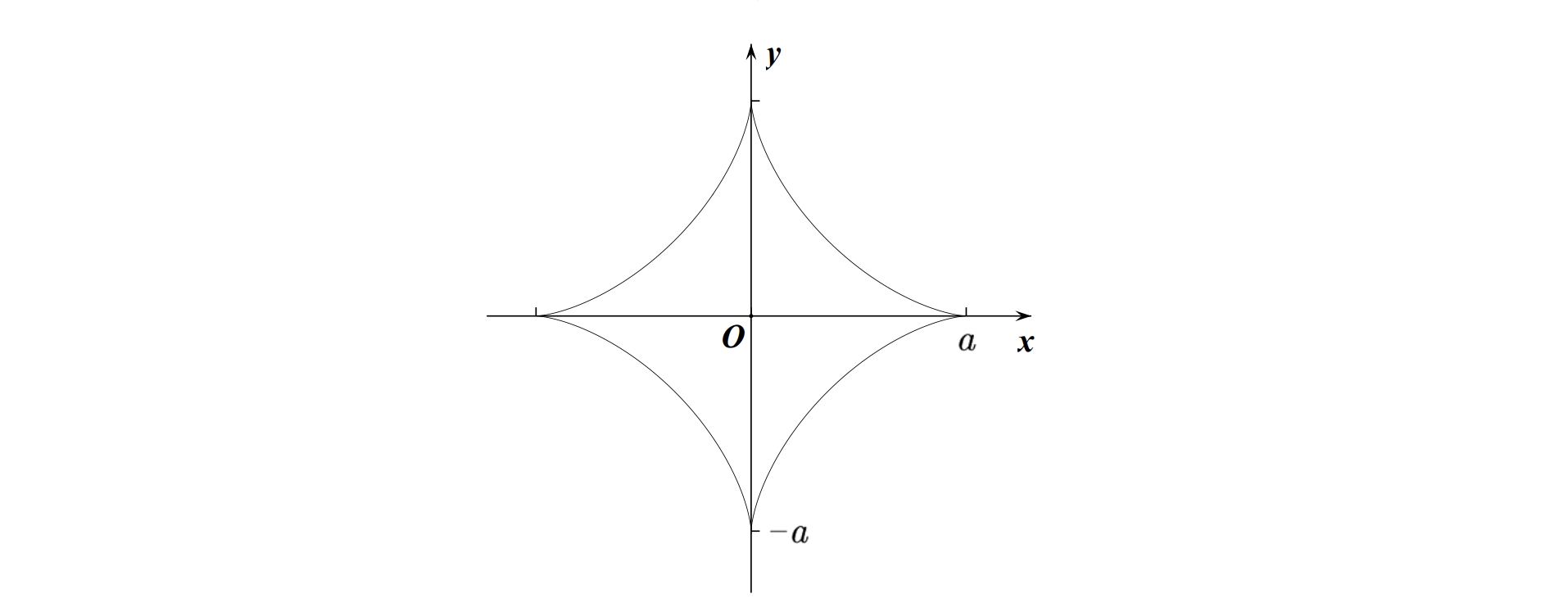
\[{1.星形线: }x^{\frac{2}{3}}+y^{\frac{2}{3}}=a^{\frac{2}{3}} \text { ,参数方程 }\left\{\begin{array}{l}
x=a \cos ^{3} \theta \\
y=a \sin ^{3} \theta
\end{array}\right. \text {. }
\]
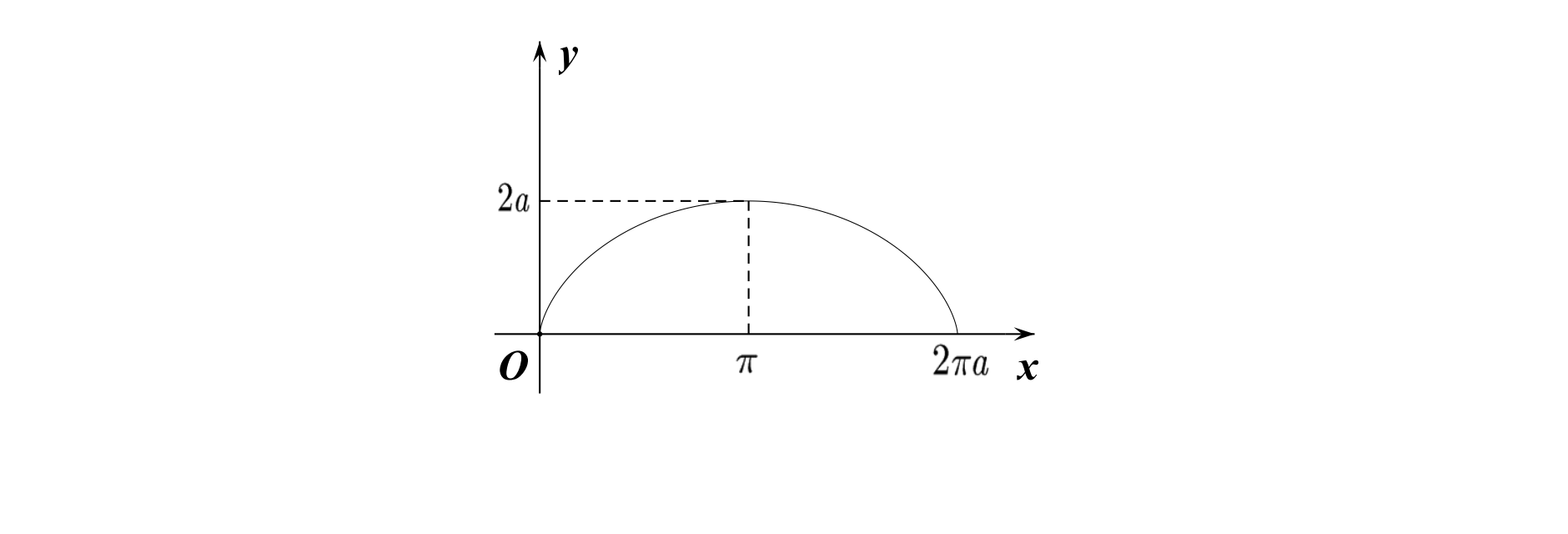
\[\text {2. 摆线:参数方程 }\left\{\begin{array}{l}
x=a(\theta-\sin \theta) \\
y=a(1-\cos \theta)
\end{array}\right. \text {. }
\]
\[\text { 3. 心形线: } x^{2}+y^{2}+a x=a \sqrt{x^{2}+y^{2}} \text {, 极坐标 } \rho=a(1-\cos \theta) \text {. }
\]
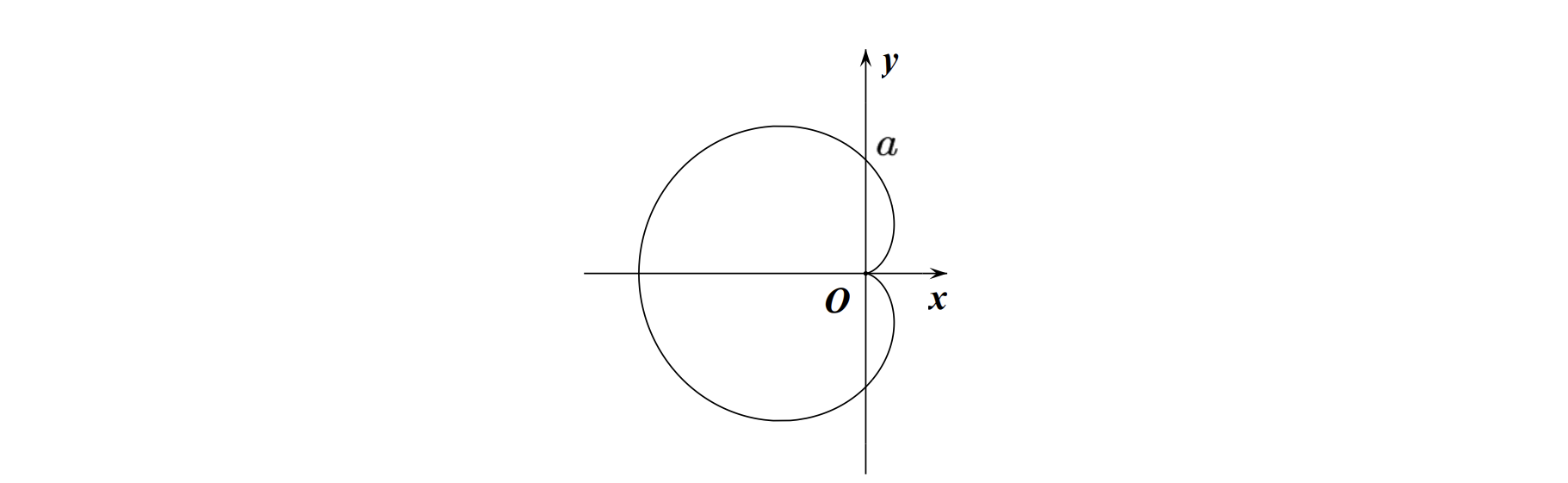
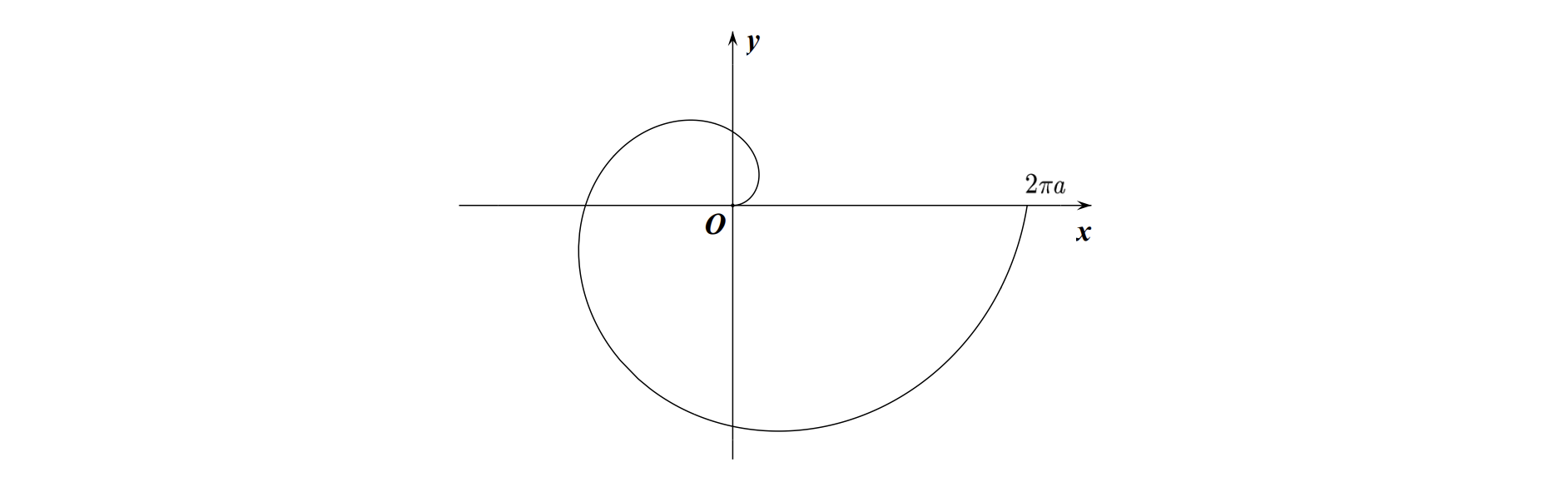
\[\text { 4. 阿基米德螺线:极坐标 } \rho=a \theta \text {. }
\]
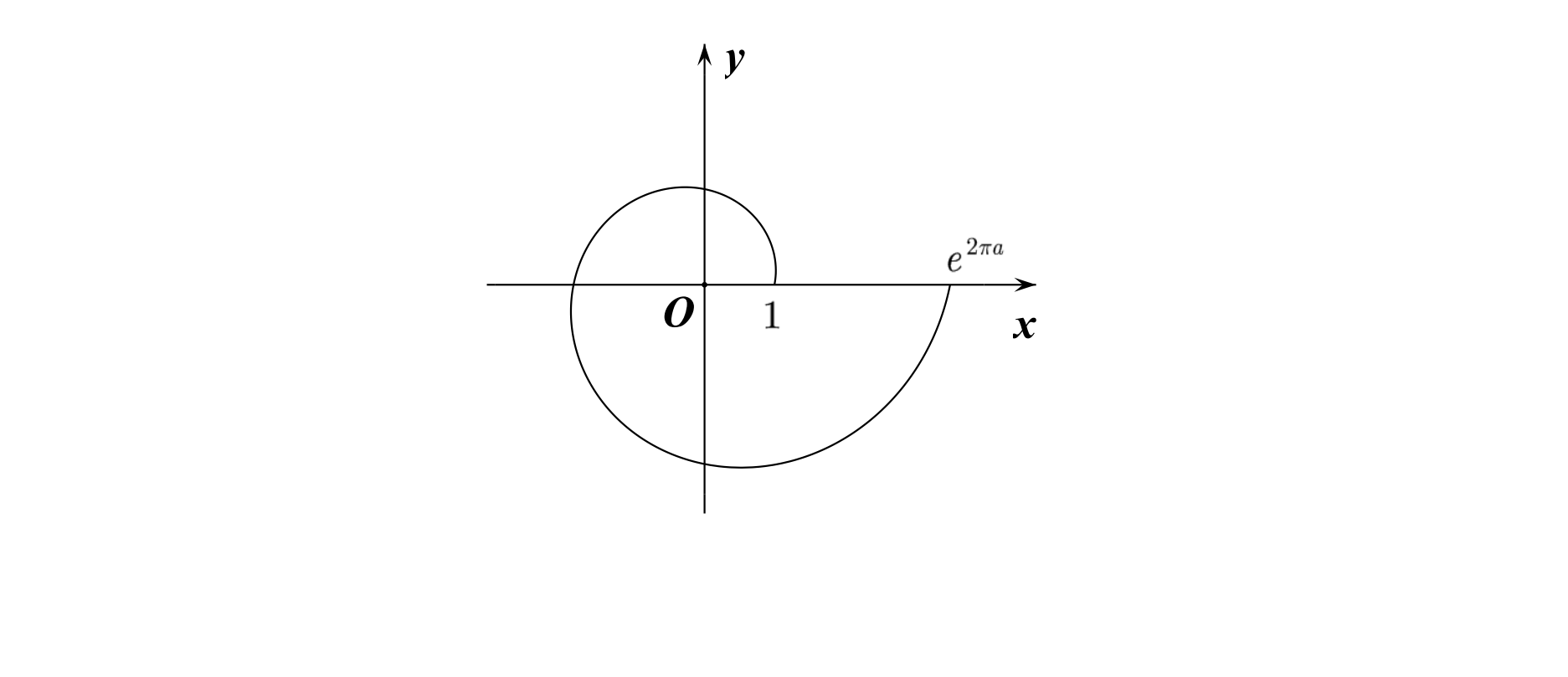
\[\text { 5.对数螺线:极坐标 } \rho=e^{a \theta} \text {. }
\]
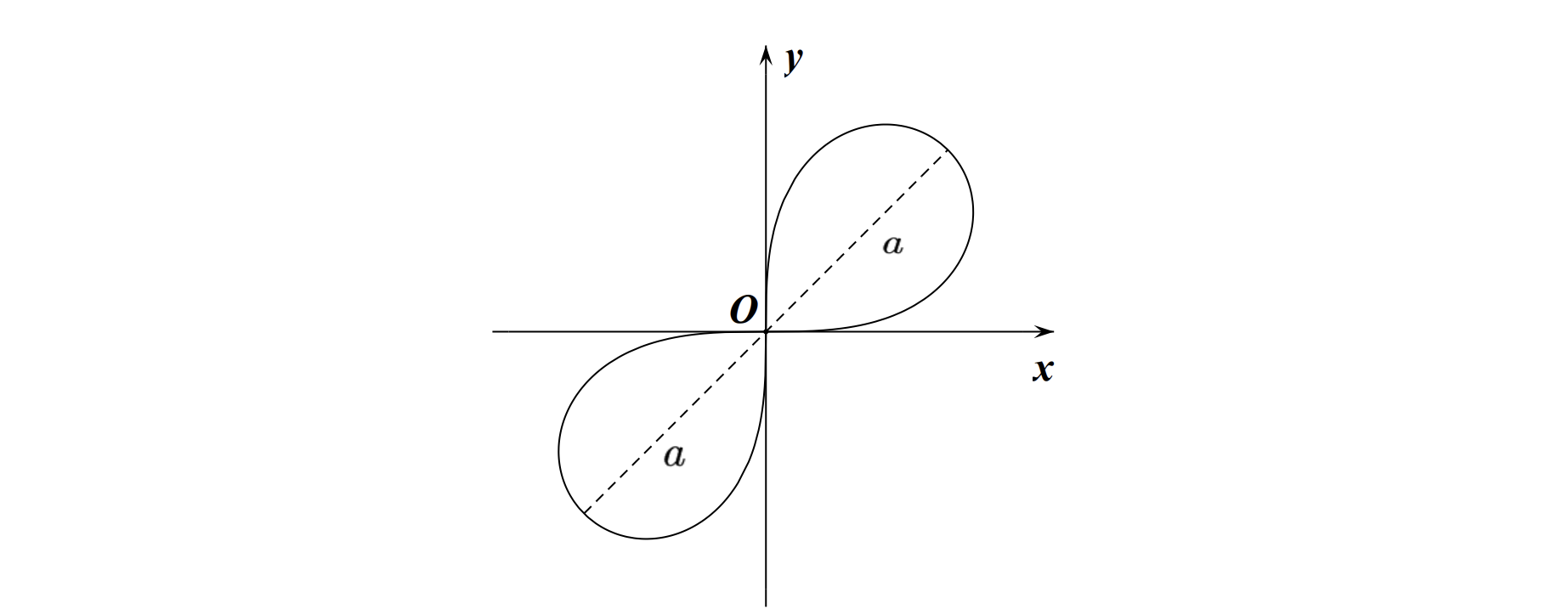
\[\text { 6.伯努利双纽线: }\left(x^{2}+y^{2}\right)^{2}=2 a^{2} x y \text {, 极坐标 } \rho^{2}=a^{2} \sin 2 \theta \text {. }
\]
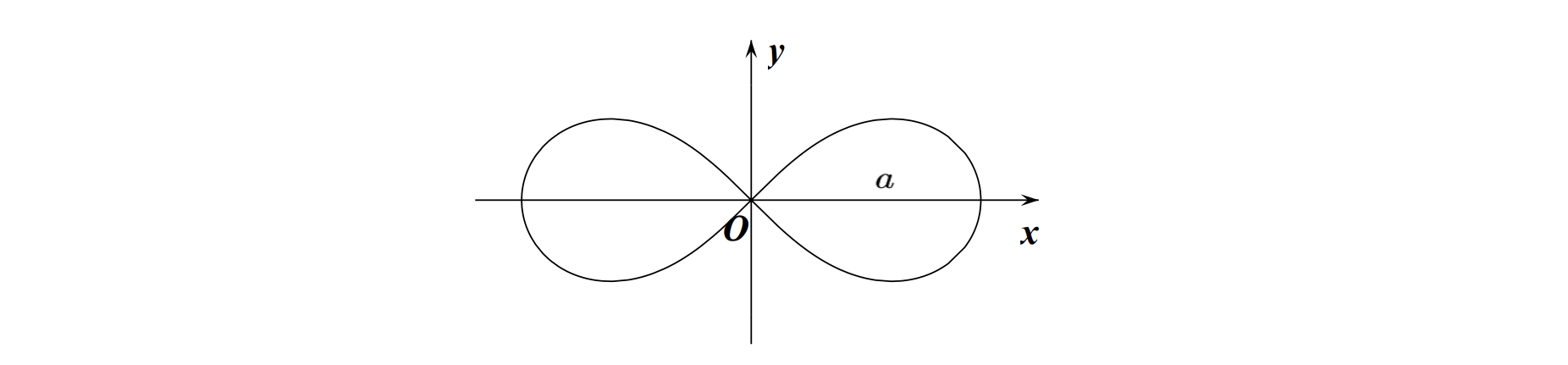
\[\text { 7. 伯努利双纽线: }\left(x^{2}+y^{2}\right)^{2}=a^{2}\left(x^{2}-y^{2}\right) \text {, 极坐标 } \rho^{2}=a^{2} \cos 2 \theta \text {. }
\]
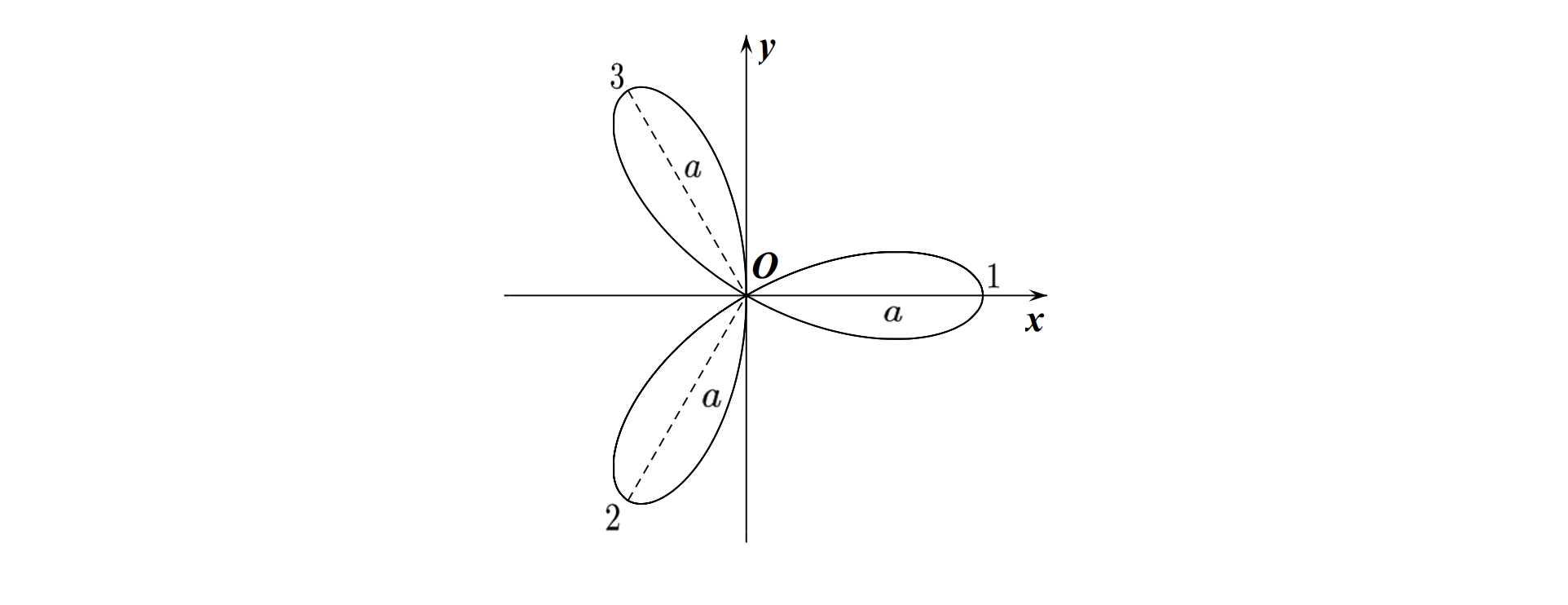
\[\text { 8. 三叶玫瑰线: 极坐标 } \rho=a \cos 3 \theta \text {. }
\]
\[\text { 9. 三叶玫瑰线: 极坐标 } \rho=a \sin 3 \theta \text {. }
\]
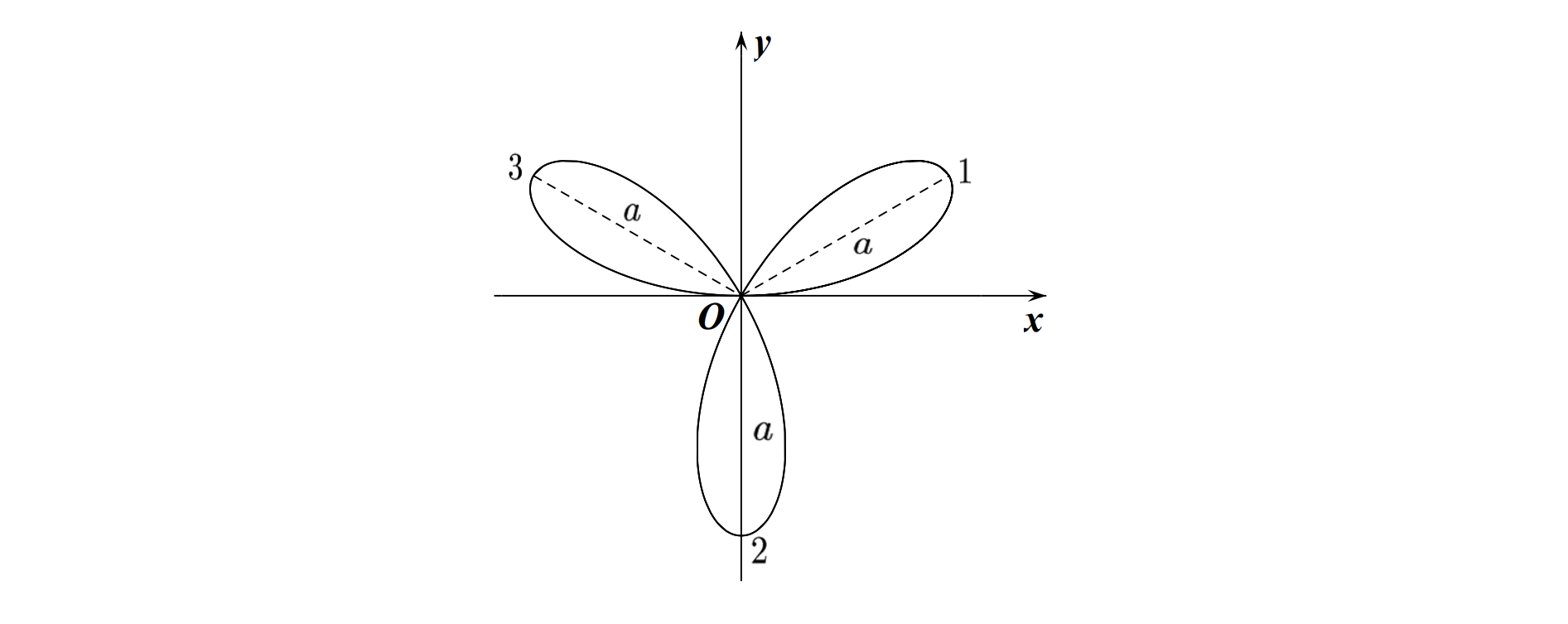
\[\text { 10. 三叶玫瑰线: 极坐标 } \rho=a \sin 2 \theta \text {. }
\]
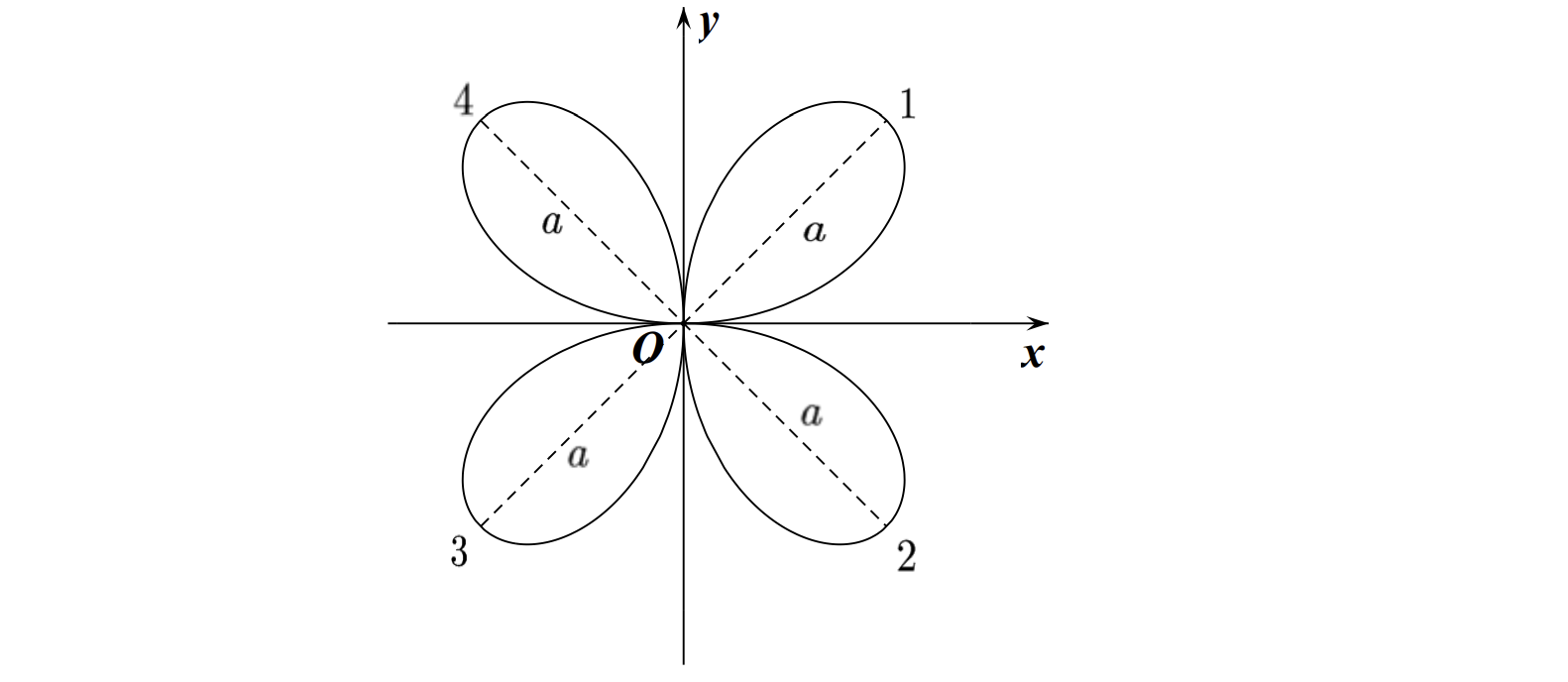
\[\text { 11. 三叶玫瑰线: 极坐标 } \rho=a \cos 2 \theta \text {. }
\]
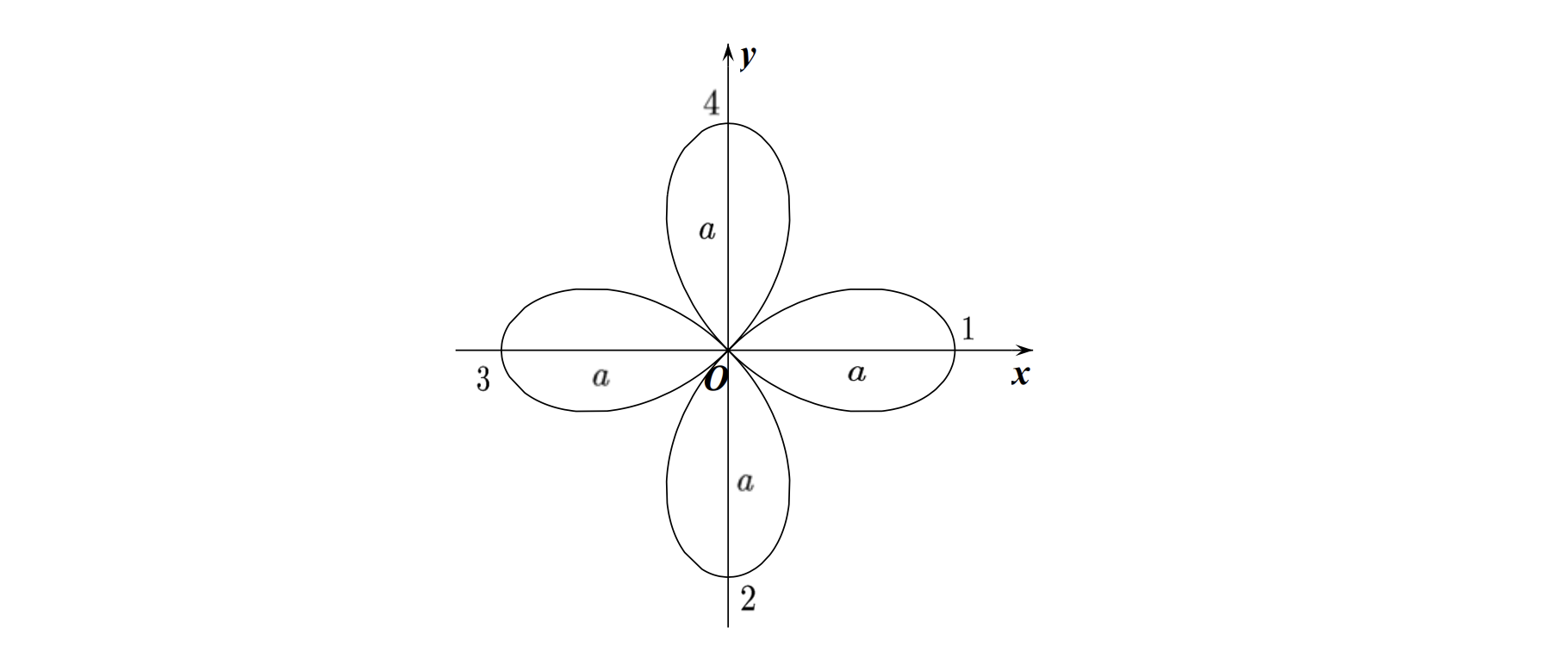
\[\text { 12.笛卡尔叶形线(第一象限部分) : } x^{3}+y^{3}-3 a x y=0 \text {,参数方程 }\left\{\begin{array}{l}
x=\frac{3 a t}{1+t^{3}} \\
y=\frac{3 a t^{2}}{1+t^{3}}
\end{array}\right. \text {. }
\]
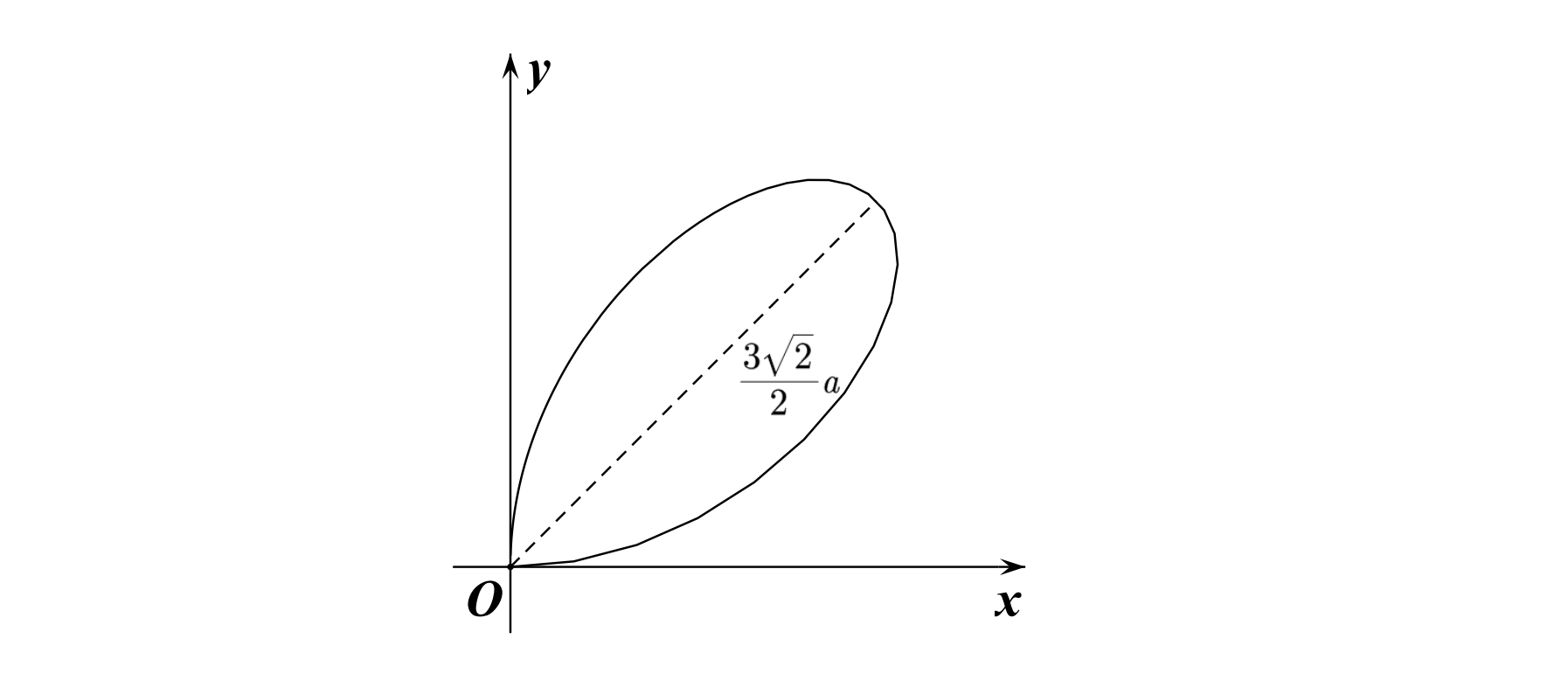
标签:right,
text,
曲线,
rho,
theta,
array,
高等数学,
极坐标,
考研
From: https://www.cnblogs.com/RioTian/p/16826090.html