博弈论入门
博弈论主要研究的是:在一个游戏中,进行游戏的多位玩家的策略。
公平组合游戏
定义:
- 游戏有两个人参加,轮流参加决策,双方均知道游戏的完整信息;
- 任意一名玩家在某一状态可以做出的决策集合只与当前状态有关,与游戏者无关;
- 游戏中某一状态不可能多次抵达,游戏以玩家无法行动为结束,且游戏一定会在有限步后以非平局结束。
\(Nim\) 游戏
\(Nim\) 游戏便是一个典型的公平组合游戏。
\(n\) 堆石子,分别有 \(a_1,a_2,a_3,a_4...a_n\) 个石子,两个玩家分别取走任意一堆的任意个石子,但不能不取。取走最后一个石子的人获胜。
博弈图与状态
如果将每个状态视作一个点,再将其与其后续状态连边则得到一个博弈状态图。
若将节点 \((i,j,k)\) 表示局面 \(i,j,k\) 时的状态,则可以这样表示博弈状态图:
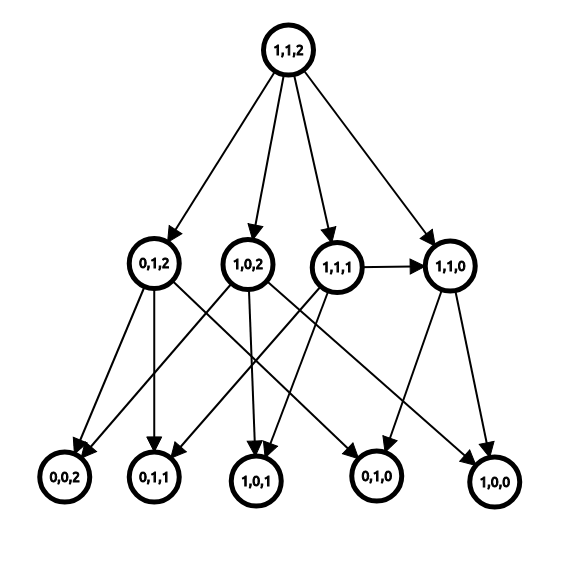
定义 必胜状态(后简称 \(N\) ) 为先手必胜的状态,必败状态(后简称 \(P\) )为先手必败的状态。
易得以下三个结论:
- 没有后继状态的状态是 \(P\) 。
- 一个状态是 \(N\) ,当且仅当存在至少一个 \(P\) 为它的后继结点。
- 一个节点是 \(P\) ,当且仅当它的后继结点都为 \(N\) 。
对于定理一,若游戏进行不下去了,则此玩家输掉游戏。
对于定理二,如果该状态至少有一个后继状态为 \(P\) ,则玩家可以通过操作到该 \(P\) 状态,则对手一定是 \(P\) 状态——对手一定失败,自己就赢得了胜利。
对于定理三,如果不存在一个后继结点为 \(P\) ,则无论如何操作,只能达到 \(N\) ,则对手一定是 \(N\) 状态——对手一定胜利,则自己一定失败。
\(Nim\) 和
让我们再次回到 \(Nim\) 游戏。
通过绘画博弈图,我们可以在 \(O(\prod_{i=1}^n a_i)\) 的时间里求出该局面是否先手必赢。
但是,这样时间复杂度实在太高。有没有更好的方法呢?
定义 \(Nim\) 和 \(=a_1 \oplus a_2 \oplus a_3 \oplus ... \oplus a_n\) 。0
当且仅当 \(Nim\) 和为零时,该状态为必败状态,否则为必胜状态。
证明
为什么异或的结果会与胜负有关?
要解决这个问题,只需证下面三个定理:
- 没有后继状态的状态是 \(P\) 。
- 对于 \(a_1 \oplus a_2 \oplus ... \oplus a_n \ne 0\) 的局面,一定存在某种移动使 \(a_1 \oplus a_2 \oplus ... \oplus a_n = 0\) 。
- 对于 \(a_1 \oplus a_2 \oplus ... \oplus a_n = 0\) 的局面,一定不存在某种移动使 \(a_1 \oplus a_2 \oplus ... \oplus a_n = 0\) 。
对于一,唯一无后继结点的状态为全0局面,此时 \(a_1 \oplus a_2 \oplus ... \oplus a_n = 0\) 。
对于二,假设 \(a_1 \oplus a_2 \oplus ... \oplus a_n = k \ne 0\) 。设我们将 \(a_i\) 改为 \(a_j\) 则 \(a_j=a_i \oplus k\) 假设 \(k\) 的最高位为 \(d\) 即 \(k \in [2^d,d^{d+1})\) 。根据定义,一定有奇数个 \(a_i\) 的二进制第 \(d\) 位为1。满足这个条件的 \(a_i\) 一定也满足 \(a_j > a_i \oplus k\) ,所以这是一个合法的移动。
对于三,若要将 \(a_i\) 变为 \(a_j\) ,根据异或的运算规则可以得出 \(a_i=a_j\) ,显然不是合法移动。
有向图游戏和 \(SG\) 函数
有向图游戏是一个经典的博弈游戏——实际上,大部分公平组合游戏都可以转化为有向图游戏。
在一个有向无环图上,只有一个起点,上面有个棋子,两个玩家轮流沿着有向边推动棋子,不能走的玩家判负。
定义 \(max\) 函数的值为不属于集合 \(S\) 的最小非负整数,即:
\(mex(S)=min\{x\}(x \notin S ,x \in N)\)
例如 \(mex(\{0,2,4\})=1,mex(\{1,2\}=0)\) 。
对于状态 \(x\) 和他的所有 \(k\) 个后续 \(y_1,y_2,...,y_k\) ,定义 \(SG\) 函数:
\(SG(x)=mex\{SG(y_1),SG(y_2),...,SG(y_k) \}\)
而对于由 \(n\) 个有向图组成的有向图游戏组成的组合游戏,设他们的起点分别为 \(s_1,s_2...s_n\) ,则有定理:当且仅当 \(SG(s_1) \oplus SG(s_2) \oplus...SG(s_n) \not = 0\) 时,这个游戏是先手必胜的。同时,这也是一个组合游戏的游戏状态 \(x\) 的 \(SG\) 值。
这一定理被称为 \(Sprague–Grundy\) 定理( \(Sprague–Grundy Theorem\) ),简称 \(SG\) 定理。
\(SG\) 函数的证明
使用数学归纳法。
假设对于游戏状态 \(x\) ,其当前节点 \(s_1^`,s_2^`,...s_n^`(对于任意i有s_i^`<s_ i)\) ,皆满足 \(SG\) 定理,显然当 \(SG(s_1)^`=SG(s_2)^`=...=SG(s_n)^`=0\) 时,该状态能满足 \(SG\) 定理。
只需证明对于游戏状态 \(x\) ,当其节点 \(s_1^`,s_2^`,...s_n^`\) 符合 \(SG\) 定理, \(SG\) 定理便成立。
其实可以看做一个 \(Nim\) 游戏,后略。
\(SG\) 函数的应用
\(SG\) 定理适用于 任何公平的两人游戏 ,它常被用于决定游戏的输赢结果。
计算给定的状态的 \(SG\) 值的步骤一般包括:
-
获取从此状态所有可能的转换;
-
每个转换都可以导致 一系列独立的博弈(退化情况下只有一个)。计算每个独立博弈的 \(SG\) 值并对它们进行 异或求和。
-
在为每个转换计算了 \(SG\) 值之后,状态的值是这些数字的 \(mex\) 。
-
如果该值为零,则当前状态为输,否则为赢。