反演是一种几何变换。在给出它的具体变换前，需要明确几个概念：

1. 直线是一种退化的圆，我们将直线与圆统称为广义圆

2. 所有直线交于一个点，即无穷远点 \(P_\infty\)

需要指出的是，反演中所述的无穷远点只有一个，这与射影几何中无穷个的无穷远点有一定区别

上述的定义可以给出广义圆的相切与相交的定义，也即有两个或一个交点，其中一个可能是无穷远点（需要注意的是，平行线交于无穷远点）

现在可以给出反演的定义：设 \(\omega\) 是一个圆，圆心为 \(O\) ，半径为 \(r\) ，关于 \(\omega\) 的反演是这样一个映射：

1. \(O\leftrightarrow P_\infty\)

2. \(A\leftrightarrow A'\) ，满足 \(OAA'\) 共线，且 \(OA\cdot OA'=r^2\) ， \(A,A'\) 称作关于 \(\omega\) 的反演对应点

我们也不必作出这个圆 \(\omega\) ，上述反演可以写作以 \(O\) 为反演中心， \(r\) 为幂的反演

我们将要给出一些反演的基本性质，设 \(O\) 是反演中心：

1. 过 \(O\) 的直线不变（不过，这条直线上面的点发生了一一对应的交换，只是它的形状位置而已）

2. 过 \(O\) 的圆变为不过 \(O\) 的直线，不过 \(O\) 的直线变为过 \(O\) 的圆 ，并且直线与圆过 \(O\) 的直径垂直

3. 不过 \(O\) 的圆 \(\odot O_1\) 变为另一个圆 \(\odot O_2\) ，并且 \(OO_1O_2\) 共线

要注意的是， \(O_1,O_2\) 不是反演对应点！

这些性质的证明不困难，关键是基于反演定义得到的：

\(\triangle OAB\sim \triangle OB'A'\)

建议对反演不熟悉的读者在阅读下列性质前先看看例题。

反演具有（逆向）保角性，换而言之，两个广义圆的夹角在反演前后不发生变化

两个圆 \(\odot O_1\) ，\(\odot O_2\) 的夹角 \(\theta\) 是这样定义的：

\(\large cos\theta =\frac{r_1^2+r_2^2-O_1O_2^2}{2r_1r_2}\)

若两圆有交点 \(K\) ， \(\theta=O_1KO_2\)

不过保角性并不常用，比较常见的是：

1. 相切的圆在反演后依旧相切

2. 正交的圆在反演后依旧正交，特别地，与反演圆 \(\omega\) 正交的圆在反演后形状位置不变化（但是上面的点发生了交换）

CP1

反演将圆变为直线的性质是非常有效的，我们来看看具体的问题如何寻找反演对应点

考试中不需要太多解释反演对应的关系是从何而来的

例1

\(K\) 为 \(\triangle ABC\) 中任一点，直线 \(AK\) 与 \(\odot(KBC)\) 交于 \(P\ne K\) ，同理对 \(B\) 定义 \(Q\) ， \(C\) 对应 \(R\) ， \(\triangle KQR,\triangle KRP,\triangle KPQ\) 的外心为 \(X,Y,Z\) ，证明： \(\triangle AXK,\triangle BYK,\triangle CZK\) 的外接圆三圆共轴

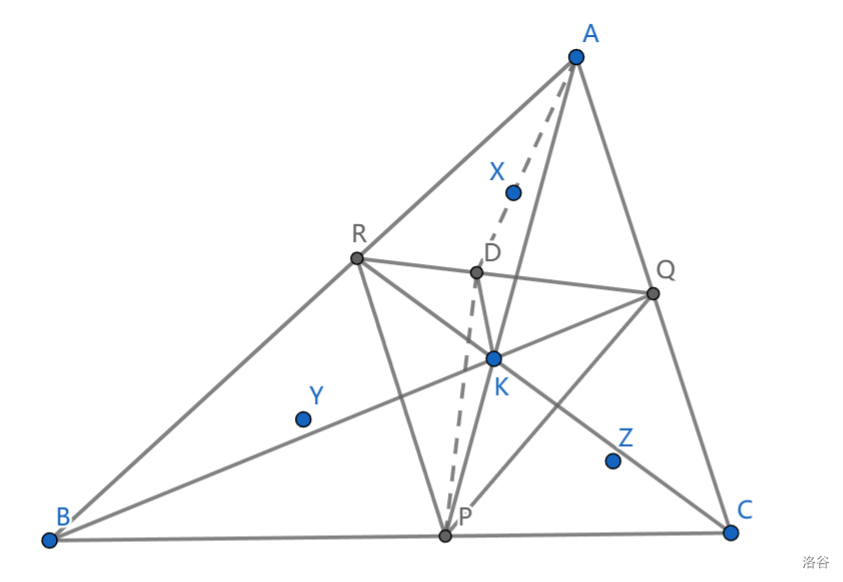
本题的人为构造痕迹非常严重，很显然是由一道正常的题目反演过来的

反演可以有效的将三圆共轴问题转变为三线共点问题，只要把三个圆反演成线就可以了

选取谁为反演中心呢？很显然是 \(K\) ，题目中的 \(9\) 个圆全部都经过它！不用在意反演幂，因为本题反演后的问题与原题没有任何联系（不会有人想去分析这9个圆的！）

1. \(\odot (KBC)\leftrightarrow B'C'\) ，同理定义另两个圆对应直线

2. \(P=\odot(KBC)\cap AK\leftrightarrow B'C'\cap A'K\) ，同理定义 \(Q,R\) 对应点

3. \(\odot (KQR)\leftrightarrow Q'R'\) ，同理定义另两个圆对应直线

4. \(X\) 的对应点比较麻烦，我们可以考虑 \(\odot (KQR)\) 的直径 \(KH\) ，现在 \(H\) 成为了 \(K\) 在 \(R'Q'\) 上的投影，而 \(KXH\) 共线且 \(KH=2KX\) 给出了 \(KX'=2KH'\) ，从而 \(X'\) 是 \(K\) 关于 \(R'Q'\) 的对称点

5. 三圆共轴 $\iff $ \(A'X',B'Y',C'Z'\) 共点

由于原图形没有用，我们不加引号分析（不要在考场上这么做！）

这里涉及一个常见的对称点处理手法，设 \(AX\cap RQ=D\) ，则 \(QD\) 是 \(\angle ADK\) 的平分线（很显然，但这个方法并不平凡）

注意到完全四边形构型，设 \(S=AK\cap RQ\) ，有 \((A,K;S,P)=-1\) ，现在有了调和点列和角平分线，自然的 \(PD\perp QR\) （这是阿氏圆构型的结论，尽管可以独立证明，但我更倾向于说这是阿氏圆）

我们将使用角元塞瓦，注意到 \(\frac {\sin \angle QAX}{\sin \angle RAX}=\frac{QD\cdot AR}{DR\cdot AQ}\) ，从而

\(\prod\limits_{cyc}\frac {\sin \angle QAX}{\sin \angle RAX}=\prod\limits_{cyc}\frac{QD\cdot AR}{DR\cdot AQ}=1\)

最后一个等号分别对 \(\triangle PQR\) 及其垂心和 \(\triangle ABC ,K\) 用了一次塞瓦 (注意 \(PD\) 是垂线，相应地另两条直线也是垂线）

例2

设四个圆 \(\omega_1,\omega_2,\omega_3,\omega_4\) 依次相切于 \(A,B,C,D\) ，证明： \(A,B,C,D\) 共圆

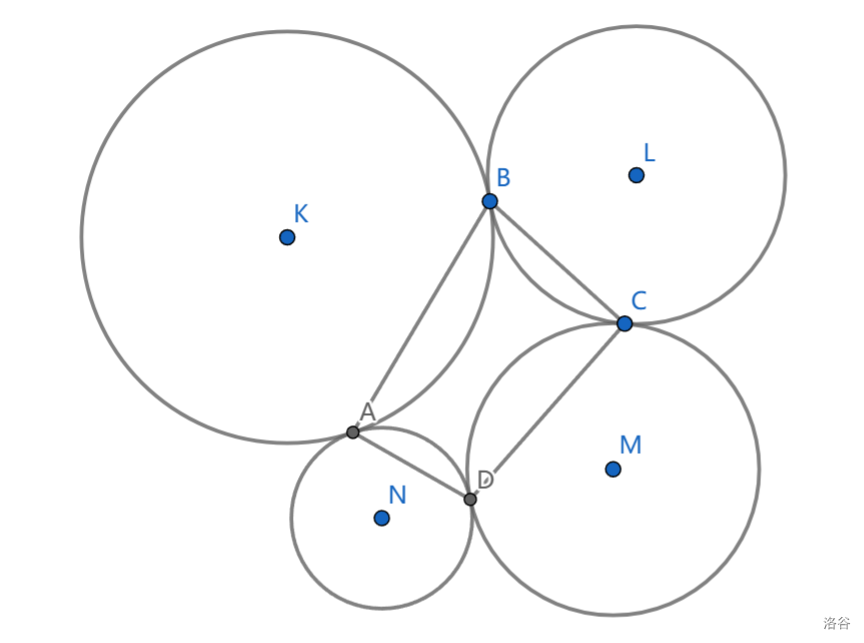
关于 \(A\) 作反演，那么 \(\omega_1,\omega_2\) 成为了两条平行直线 \(l_1,l_2\) ， \(l_1\) 与 \(\omega_3'\) 相切于 \(B'\) ， \(l_2\) 与 \(\omega_4'\) 相切于 \(D'\) ，而 \(\omega_3',\omega_4'\) 切于 \(C'\)

现在 \(\omega_3',\omega_4'\) 关于 \(C'\) 位似， \(l_1,l_2\) 又是它们的对应切线，从而 \(B',D'\) 是对应点， \(B'C'D'\) 共线，即 \(ABCD\) 共圆

尽管对解题没什么影响，但有一个问题： \(C'\) 在 \(l_1,l_2\) 之间还是之外？其实是在两者之间，因为 \(A\) 在 \(\omega_1\) 上，反演之后， \(\omega_1\) 内部的点跑到了 \(l_1\) 异于 \(A\) 一侧，而 \(\omega_1\) 外部的点跑到了 \(l_1\) 与 \(A\) 同侧， \(C\) 是在 \(\omega_1\) 外的，同理对 \(\omega_2\) 分析可得结论

例3

考虑以 \(O\) 为圆心， \(\overline{AB}\) 为直径的半圆， \(CD\) 是半圆上的弦， \(AB\cap CD=M\) ，有 \(MA>MB,MC>MD\) ，定义 \(K=\odot(AOC)\cap \odot(BOD)\) ，求证： \(\angle MKO=Rt\angle\)

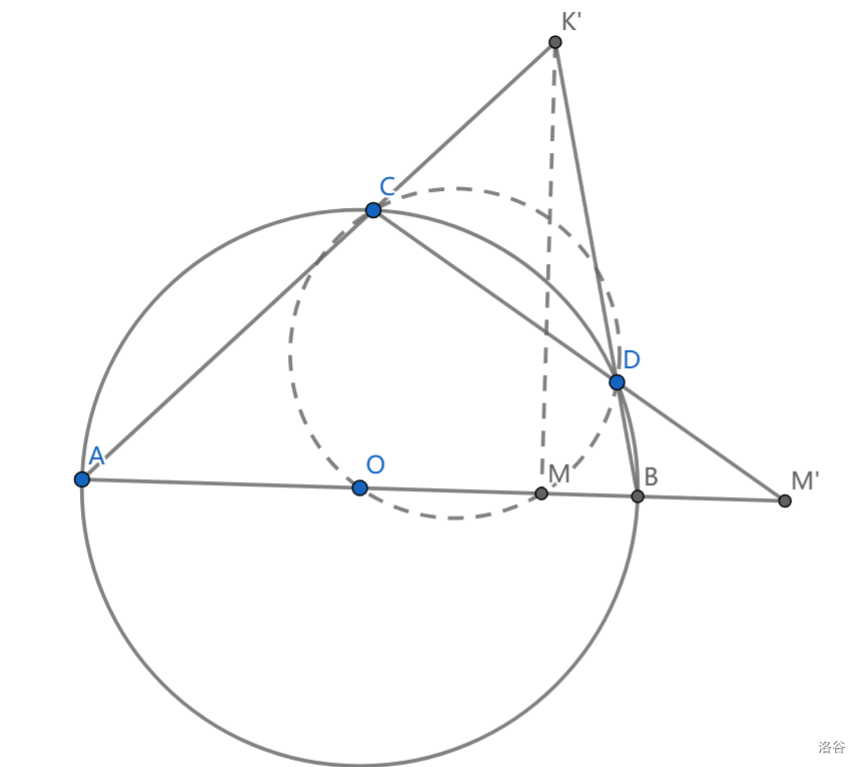
不是很容易看出可以用反演，不过，能够看出这不是那些不能用反演的题目（有很多直线与到处都是的角），所以最好试一试

反演对象很明确，是关于这个半圆（当然要补全）， \(M\) 就成为了 \(\odot(COD)\cap AB\) ， \(K\) 就成为了 \(AC\cap BD\) ，要证 \(\angle OMK=Rt\angle\)

这很显然，因为 \(\angle ACB=\angle ADB=Rt\angle\) ， \(O\) 为 \(AB\) 中点，说明 \(\odot(COD)\) 就是 \(\triangle ABK\) 的九点圆！

例4

圆 \(c_1,c_2\) 交于 \(A,B\) 两点，\(P\) 在过 \(B\) 且与 \(c_2\) 相切直线上，过 \(P\) 作 \(c_2\) 切线 \(PC\) ，作 \(c_1\) 切线 \(PD,PE\) ， \(Q=DE\cap BC\) ，求证： \(ACPQ\) 共圆

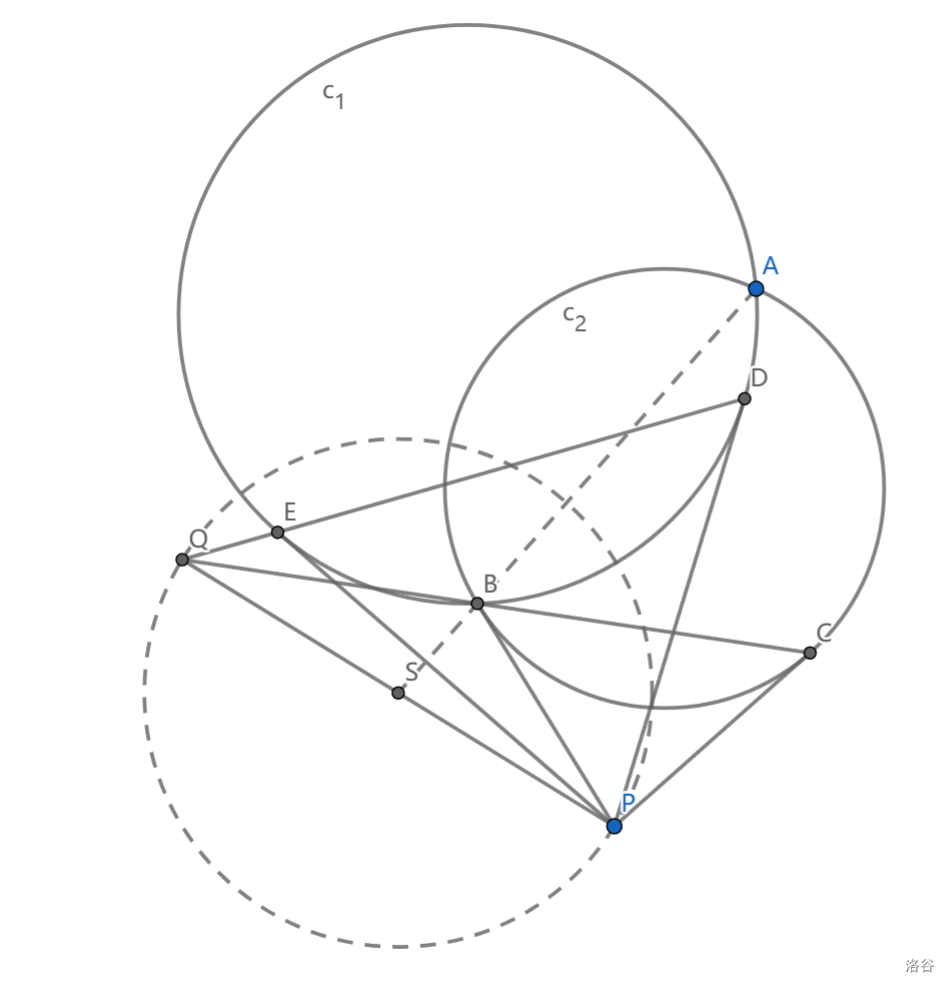
这题很容易联想到极线的共轭性质（或者配极原则，或者 La Hire 定理，不管你叫它什么），但实质需要的是这样的性质：

\(P,Q\) 关于 \(c\) 共轭 \(\iff\) 以 \(PQ\) 为直径的圆与 \(c\) 正交

极线的共轭性质证明太多了，但有一种计算（很简单的）给出了这个性质，它讲的是 \(P,Q\) 共轭 \(\iff OP^2+OQ^2-2R^2=PQ^2\)

作出这个圆（称 \(PQ\) 中点为 \(S\) ），关于 \(\odot S\) 反演后， \(c_1,c_2\) 不变（再次强调，只是形状位置），而 \(A\leftrightarrow B\) ，给出 \(ABS\) 共线，并且 \(SA\cdot SB=SQ^2\)

从而 \(\triangle AQS\sim \triangle QBS\) ，给出 \(\angle AQP=\angle AQS=\angle QBS=\angle ABC=\pi- \angle ACP\)

这个问题还说明了反演不一定要按照题目所给的构图顺序判断对应关系，甚至可以用圆的交点等刻画给出基于反演定义的性质，在后续问题中也会看到

例5

\(c_1,c_2\) 正交， \(c_1\) 的直径 \(AB\) 满足 \(B\) 在 \(c_2\) 内部，经过 \(OA\) 的两圆与 \(c_2\) 切于 \(F,G\) ，求证： \(FOGB\) 共圆

关于 \(c_1\) 反演，只要证 \(B\) 在 \(A\) 关于 \(c_2\) 的极线上（因为 \(c_2\) 形状位置不变），只要 \(A\in l_B\)

延长 \(O_2B\) 交 \(c_1\) 于 \(B'\) ，两圆正交给出 \(O_2B\cdot O_2B'=O_1O_2^2-R^2=r^2\) ，即 \(B,B'\) 是关于 \(c_2\) 的反演对应点，再由 \(\angle AB'B=Rt\angle\) 给出 \(AB'=l_B\)

CP2

反演在处理一些奇怪的角度关系时也是有效的工具。前提是，这些角的边大多会经过反演点，并且反演有时会将简单的相等关系转换的复杂，对于正常的（但毫不相干的）两个等角应当慎用

例1

设 \(A,B,C,D\) 是平面上四个点， \(C,D\) 在直线 \(AB\) 同一侧，满足 \(AC\cdot BD=AD\cdot BC\) ， \(\angle ADB=\angle ACB+90\degree\) ，求 \(\frac{AB\cdot CD}{AC\cdot BC}\) 的值，并证明 \(\odot(ACD),\odot(BCD)\) 正交

我们将展示反演如何将两个条件变得极其的优美：关于 \(A\) 作反演，有 $\angle AB'D'=\angle AB'C'+90\degree\iff \angle C'B'D'=Rt\angle $ ， \(\frac{AC}{BC}=\frac{AD}{BD}\iff \frac{AB'}{B'C'}=\frac{AB'}{B'D'}\iff B'C'=B'D'\)

那么 \(\frac{AB}{BC}\cdot \frac{CD}{AD}=\frac{AC'}{B'C'}\cdot \frac{C'D'}{AC'}=\sqrt 2\) ，正交由保角性显然

注：标准答案是使用旋转相似

例2

设 \(P\) 在 \(\triangle ABC\) 的内部，满足 \(\angle APB-\angle ACB=\angle APC-\angle ABC\) ，设 \(D,E\) 是 \(\triangle APB,\triangle APC\) 的内心，求证： \(AP,BD,CE\) 共点

题目条件 \(\iff \angle CAP+\angle CBP=\angle BAP+\angle BCP\) ，关于 \(P\) 反演，等价于 \(\angle A'B'P+\angle C'B'P=\angle A'C'P+\angle B'C'P\iff \angle A'B'C'=\angle B'A'C'\)

从而 \(\frac{AB}{AP}=\frac{A'B'}{A'P}=\frac{A'C'}{A'P}=\frac{AC}{CP}\) ，由角平分线定理完成证明。

注：直接作 \(\triangle ABC\) 的外接圆就可以把这两个角移到一块了，或许本题还不足以展示反演在处理角条件时的强大，下面的例题就不大一样了

例3

点 \(C\) 在 \(\triangle PAD\) ，点 \(S\) 与 \(T\) 分别在 \(AC,AD\) 上，线段 \(CT,DS\) 交于点 \(B\)，满足 \(\angle CPD+\angle APB=\angle ASD,\angle CPD-\angle APB=\angle ATC\) ， \(Q\) 是 \(\odot(PAB),\odot(PCD)\) 另一交点，求证： \(PSQT\) 共圆

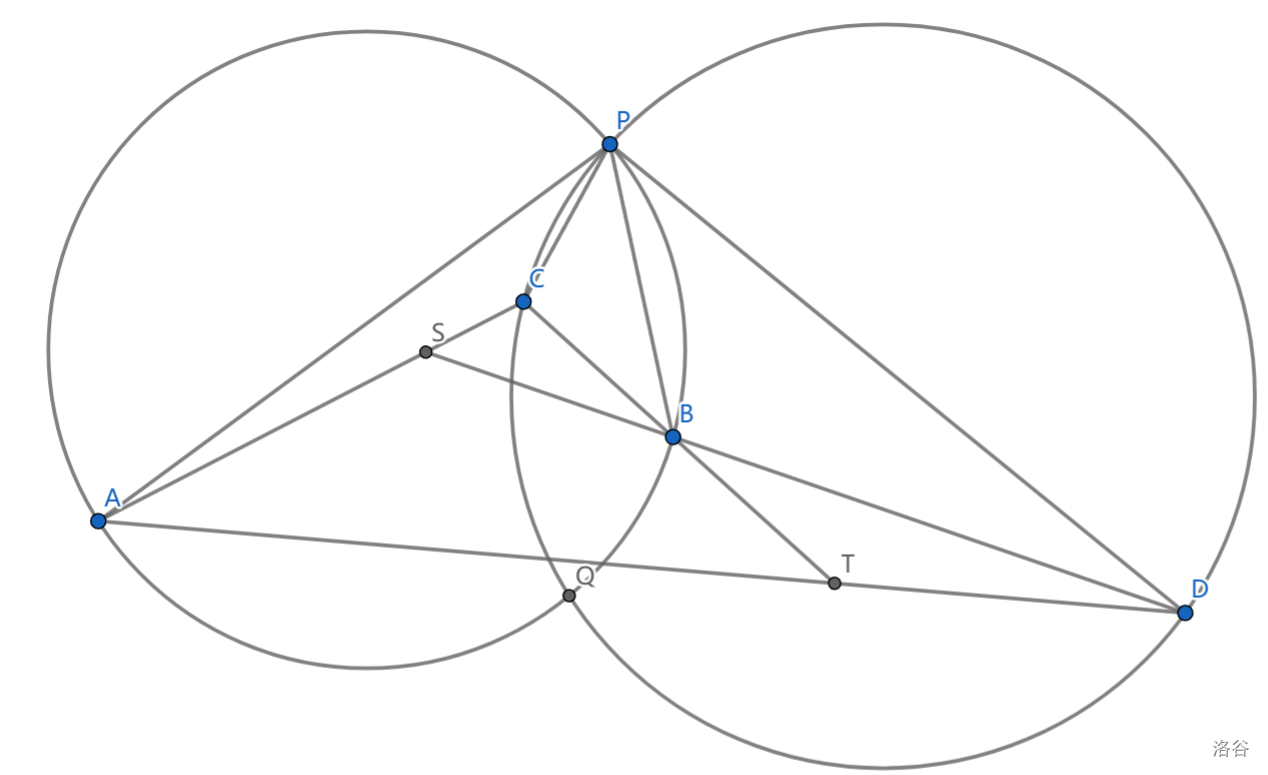
（此图仅作示意）

这题的圆和直线都不少，不过 \(\angle CPD+\angle APB=\angle ASD\iff \angle BPC=\angle PAC+\angle PBD\)

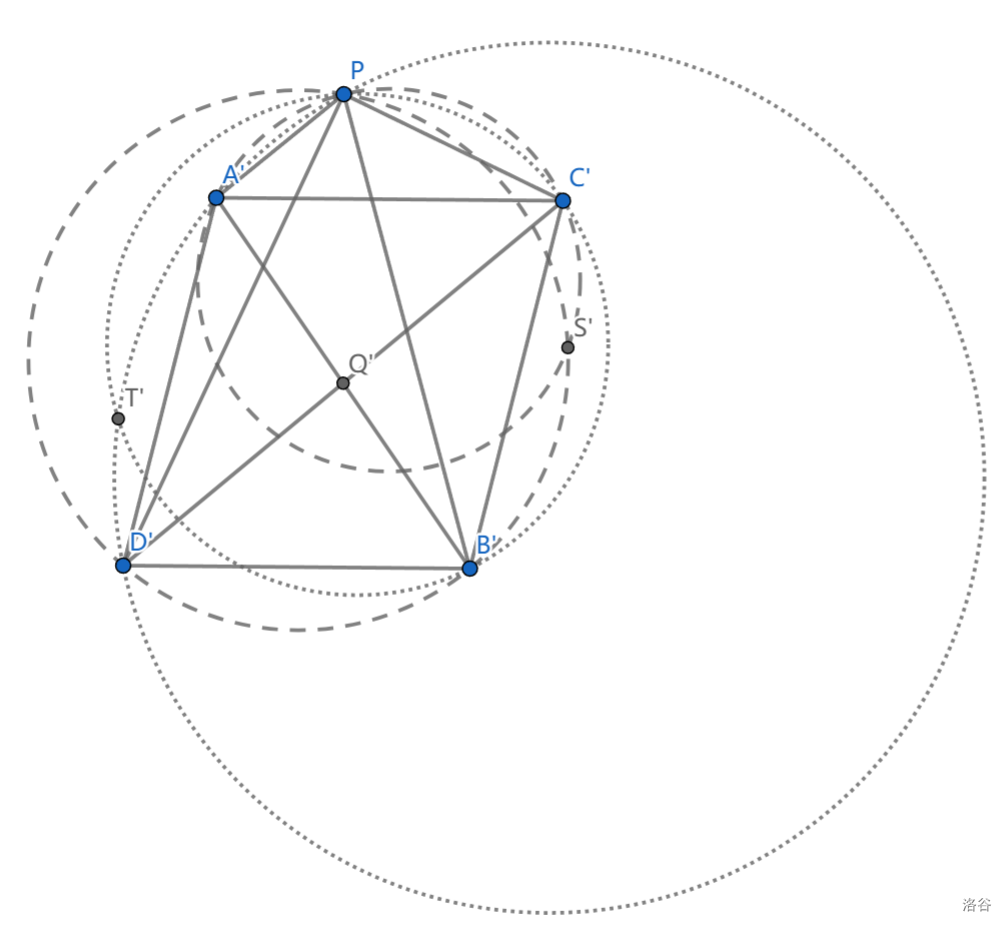
现在关于 \(P\) 反演，就可以看到一个在初中学习平行线时就给出的构型！具体地，得到 \(\angle B'PC'=\angle PC'A'+\angle PD'B'\) ，进而 \(A'C'//B'D'\)

同理 \(A'D'//C'B'\) ，得到平行四边形 \(A'C'B'D'\) ，中心为 \(Q'\) ，接下来需要大胆猜测（或者说在图上看出来）的是 \(S',T'\) 也是关于 \(Q\) 对称的（我们要证它们三点共线），令 \(T''\) 是 \(S'\) 关于 \(Q\) 的对称点，我们将证明 \(T''\) 属于圆 \((PA'D'),(PC'B')\)

来看看 \(\angle C'T''B'\) ，根据对称，它 \(=\angle A'S'D'=\angle S'A'C'+\angle S'B'D'=\angle S'P'C'+\angle B'P'S'=\angle B'P'C'\) ，则 \(PB'C'T''\) 共圆，同理 \(PA'D'T''\) 共圆，证毕

CP3

内切圆反演

关于内切圆 \(\odot I\) 的反演将外接圆变为切触三角形 \(\triangle DEF\) 的九点圆（由 \(A\) 关于内切圆极线为 \(EF\) ，且 \(AI\) 垂直平分 \(EF\) 可知）

伪内切圆切点变为 \(D\) 与垂心连线的中点

例1

三角形 \(\triangle ABC\) 内切圆切三边于 \(D,E,F\) ， \(Q\) 是 \(\triangle ABC\) 外接圆上 \(A\) 的对径点， \(QI\cap EF=P\) ，求证： \(DP\perp EF\)

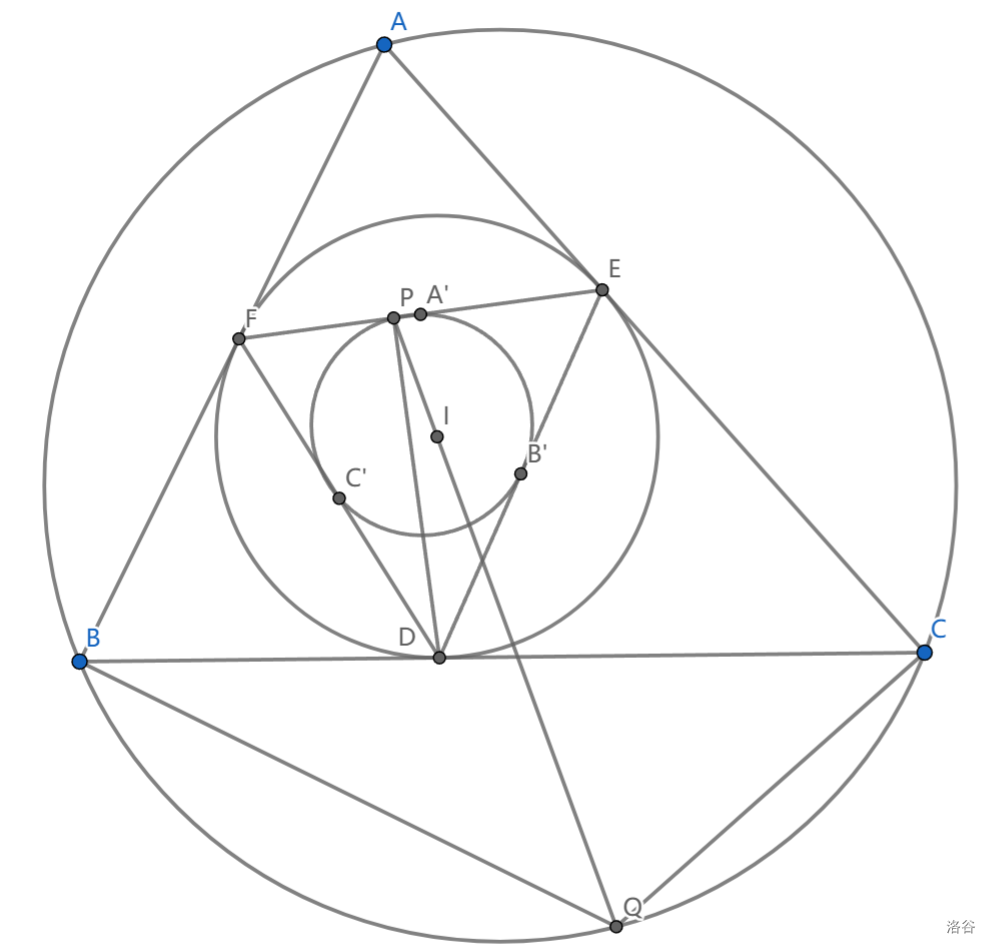
设 \(QI\cap \odot(ABC)=P'\) ，我们将证明 \(P,P'\) 是关于内切圆的反演对应点。，这直接由 \(P\in l_A,AP'\perp IP\) 得到

于是 \(P\) 是 \(\triangle DEF\) 九点圆上的点，而 \(P\ne A\) ，从而 \(P\) 是垂足，证毕

垂心反演对称

设锐角三角形 \(\triangle ABC\) 满足 \(AB>AC\) ，外接圆为 \(\omega\) ， \(D\) 是 \(A\) 在 \(BC\) 上的投影， \(M\) 是 \(BC\) 上的投影， \(Q\) 在 \(\omega\) 上且满足 $\angle HQA=Rt\angle $ ， \(K\) 在 \(\omega\) 上且满足 \(\angle HKQ=Rt\angle\)， \(A,B,C,K,Q\) 在 $\omega $ 上按一个方向排列，求证： \(\odot(KQH)\) 与 \(\odot(FKM)\) 相切

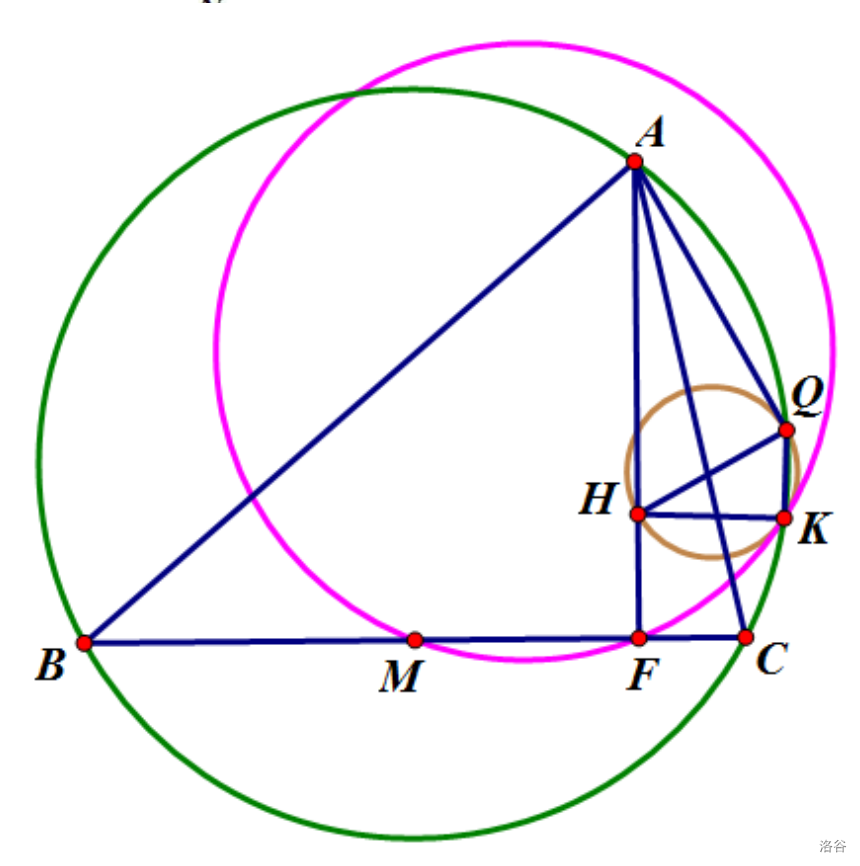
我们默认读者已经知晓（并清楚如何证明）： \(H\) 关于 \(\triangle ABC\) 三边对称点在 $\omega $ 上； \(MHQ\) 共线

关于 \(H\) 以 \(\sqrt{HA\cdot HD}\) 为幂反演，并将图形关于 \(H\) 中心对称，根据上述性质，可以验证：

\(A\leftrightarrow D,B\leftrightarrow E,C\leftrightarrow F,M\leftrightarrow Q\)

\(\odot (KQH)\) 成为了与 \(HQ\) 垂直的一条直线（因为 \(HQ\) 原来是它的直径），过 \(M\) 做 \(l\) 垂直于 \(MQ\) 交 \(\odot(MEF)\) 于 \(K'\)

则 \(K=\odot(直径QH)\cap\odot(ABC)\leftrightarrow K'=l\cap \odot(DEF)\)

设 \(AH\) 中点是 \(N\) ，中位线给出 \(NE=\frac 12\) 及 \(NE\perp MQ\) ，在九点圆内有矩形 \(K'MEN\) ，从而 \(K'A=K'Q\) （垂直平分），即 \(MK'\) 与 \(\odot(AQK)\) 相切，反演回去得到题目欲证。

伊朗式反演

对三角形 \(\triangle ABC\) ，以 \(A\) 为反演中心， \(\sqrt{AB\cdot AC}\) 为幂的反演叠加上关于 \(\angle BAC\) 角平分线的对称被称为伊朗式反演，或者强制对称变化

关键是 \(B,C\) 互为对应点，并且将外接圆变为了直线 \(BC\) ，这在处理伪内切圆时很有帮助

例1

\(\triangle ABC\) 内接于 \(\Gamma\) ， \(S_b,S_c\) 分别是劣弧 \(AB,AC\) 的中点， \(\omega_b\) 切 \(\Gamma\) 于 \(S_b\) 并与 \(AB\) 相切， \(\omega_b\) 切 \(\Gamma\) 于 \(S_c\) 并与 \(AC\) 相切，求证： \(\omega_b,\omega_c\) 的根轴过伪内切圆切点 \(T\)

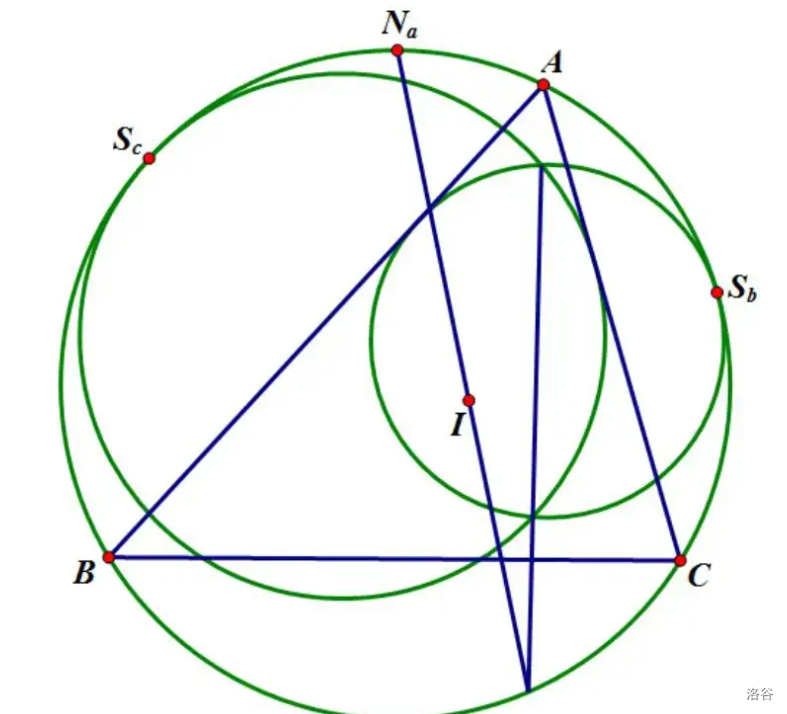
本题有初等几何证法，难度大概在高联 \(T2.5\) ，但是伊朗式反演可以直接“秒杀”

关于 \(\triangle ABC\) 作伊朗反演，设 \(S_b\leftrightarrow M,S_c\leftrightarrow N\)

则 \(\angle NAC=\angle S_cAB=\frac 12C\) ，从而 \(\triangle NAC\) 是等腰三角形，同理 \(\triangle MBA\) 是等腰三角形

来看看伪内切圆到哪去了，它现在与 \(AB,AC,BC\) 相切，它原来在 \(\Gamma\) 内，现在就应当在 \(BC\) 下侧，成为旁切圆，切点是 \(T'\)

\(\omega_b'\) 现在与 \(BC\) 相切，切点是 \(N\) ， \(\omega_c'\) 与 \(BC\) 切于 \(M\) ，欲证 \(T'\) 在两圆根轴，只要做两件事：

1. 证明 \(A\) 在根轴上，从而根轴还是直线

2. 证明 \(T'\) 在根轴上，即 \(T'M=T'N\) ，这是显然的

设 \(\omega_c\) 切 \(AC\) 于 \(X\) ， \(\omega_b\) 切 \(AB\) 于 \(Y\) ，由位似关系， \(S_bXYS_c\) 共线，而 \(A\) 在根轴上等价于 \(AX=AY\) ，这是显然的，证毕。

这个方法的唯一思维量在于证明 \(A\) 在两圆根轴上！

例2

\(D,E,F\) 是 \(\triangle ABC\) 上三点， \(I\) 是凸四边形 \(BCEF\) 内一点，满足 \(AFIE\) 共圆，设 \(EF\) 交 \(\odot(ABC)\) 于 \(P,Q\) ，若 \(\frac{BF}{FI}\cdot \frac{IE}{EC}\cdot \frac{CD}{DB}=1\) ，求证： \(\angle APD+\angle AQD=\angle PIQ\)

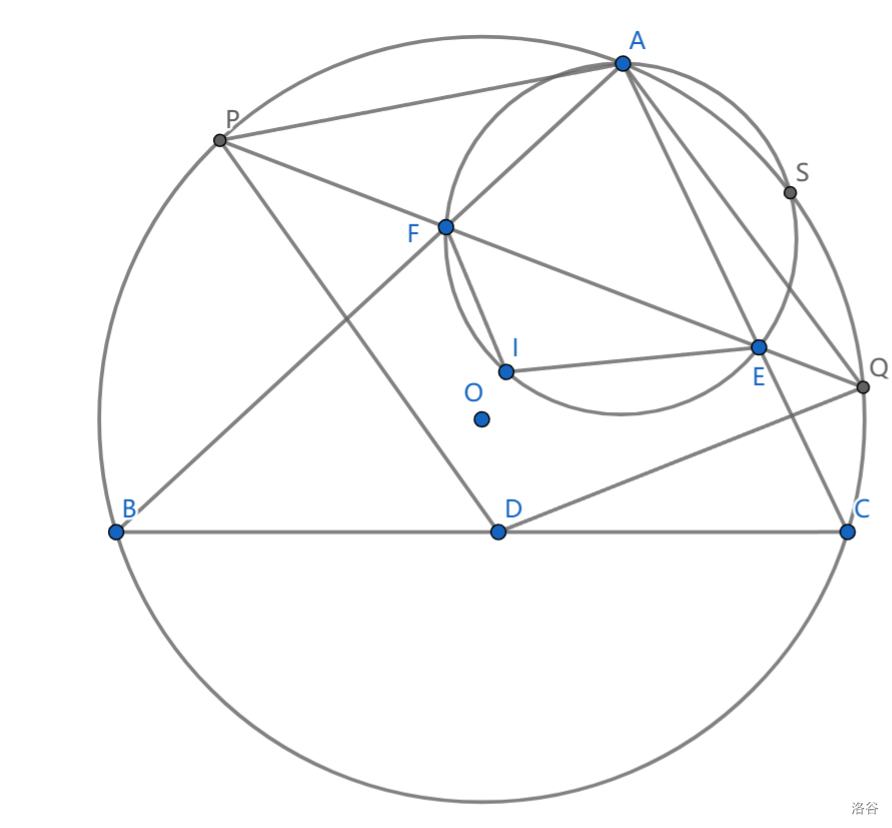
这样奇怪的条件与求证不难联想到反演，可以看到 \(A\) 上有很多圆，但如果你从 \(A\) 出发反演，那你就完蛋了，因为点 \(D\) 会无法跟踪

构造四边形 \(BCEF\) 的密克点 \(S\) ，这样做的好处是旋转相似 \(\triangle SFB\sim \triangle SEC\) 给出 \(\frac{BF}{EC}=\frac {SF}{SE}\) ，关于 \(\triangle SFC\) 作伊朗式反演， \(C\leftrightarrow F,B\leftrightarrow E\)

现在 \(EF\leftrightarrow \odot(ABC)\) ，则 \(P\leftrightarrow Q\) ，而 \(\odot(AEF)\leftrightarrow BC\) 给出 \(I'\in BC\)

是时候使用题目的比例条件了，我们有 \(\frac{SI'}{CI'}\cdot \frac{BI'}{SI'}\cdot \frac{CD}{DB}=1\) ，从而 \(I'=D\) ！

现在一切都已处理完毕，通过反演得到了 \(\angle APD+\angle AQD=\angle AIQ+\angle AIP\) ，显然等于 \(\angle PIQ\) ，证毕。