Tarjan 与连通性

标签：Tarjan 连通性 int 割点 SCC dfn low 节点

tarjan 是一系列与图连通性相关的算法的统称，本文将总结常见的 tarjan 算法。并配合一定量的练习。

无向图求割边割点

割点：删掉后让整个图不联通的点。

割边（桥）：删掉后让整个图不联通的边。

搜索树：对图进行 dfs 时经过的边的集合。容易发现其构成一棵树。搜索树上的边称为树边。

时间戳：对图进行 dfs 时经过的点的时间。

追溯值：这里，定义其为以下节点的时间戳的最小值。

x 的子树的节点。
x 的子树的节点通过一条非树边能到达的点。

（PS：追溯值在不同的 tarjan 中定义不同）

这里，x 的追溯值的含义其实就是 x子树上的点不走 (x,fa[x]) 能到的所有点的时间戳的 min。

追溯值的求法：

先令 low[x]=dfn[x]，考虑每条 (x,y)：
1. 若其是树边，则令 low[x]=min(low[x],low[y])。
2. 若其不是树边，则令 low[x]=min(low[x],dfn[y])。

解释：回头看定义。

割边判定法则

(x,y) 是割边，当且仅当 dfn[x]<low[y]。

感性理解一下，根据追溯值的含义，y 的子树不在通过 (x,y) 的情况下，一步走不到 x 及之前的点，完全可以说明 (x,y) 将图分成两边。

不难发现，割边一定是树边，且简单环上的边一定不是割边。

割边判定法则的几何意义：删掉这条边能把这条边的子树割出去。

求割边实现

void tarjan(int u, int in) // 记录入边
{
	dfn[u] = low[u] = ++num; // 初始 low=dfn
	for (int i = head[u]; i; i = e[i].nxt)
	{
		int v = e[i].v;
		if (!dfn[v]) // 对没访问过的点跑 tarjan
		{
			tarjan(v, i);
			low[u] = min(low[u], low[v]);
			if (low[v] > dfn[u])			   // 割边判定法则
				bridge[i] = bridge[i ^ 1] = 1; // 该条边和其反向边都是割边
		}
		else if (i != (in ^ 1)) // 不会用父亲更新
			low[u] = min(low[u], dfn[v]);
	}
}

割点判定法则

x 不是搜索树的根节点

当且仅当 x 存在一个子节点 y 使得 dfn[x]<=low[y]。
x 是搜索树的根节点

当且仅当 x 存在两个子节点 y 使得 dfn[x]<=low[y]。

y 的子树走一步最多到 x，可判定割点。

对根节点来说，至少有两个子树才可能是割点。

因为割点判定法则是小于等于号，所以不用考虑入边和父亲的问题。

割点判定法则的几何意义：删掉这个点能把这条边的子树割出去。

求割点实现

void tarjan(int u)
{
	dfn[u] = low[u] = ++num; // 初始 low=dfn
	int flag = 0;			 // 记录满足割点判定法则的点的个数（用于搜索树的根节点割点判定）
	for (int i = head[u]; i; i = e[i].nxt)
	{
		int v = e[i].v;
		if (!dfn[v])
		{
			tarjan(v); // 对没访问过的点 tarjan
			low[u] = min(low[u], low[v]);
			if (low[v] >= dfn[u]) // 割点判定法则
			{
				flag++;
				if (u != root || flag > 1) // 要么不是根节点，要么是根节点且满足多个
					cut[u] = 1;
			}
		}
		else
			low[u] = min(low[u], dfn[v]); // 访问过的也可以用于更新 low，但不是搜索树的子节点所以只能用 dfn
	}
}

联通分量的几何认识：

边双：无向环套环（连接处可以是点）、孤立点。

点双：环套环（连接处要是边）、两个点相连、孤立点。

强联通分量：有向环（连接处可以是点）、孤立点。

无向图的双联通分量（DCC）

边双连通图（边双 e-DCC）：没有割边的图。

点双连通图（点双 c-DCC）：没有割点的图。

分量：不能再扩展的子图。

求边双

非常简单，把所有割边都删掉，每个连通块就是一个边双。

实现上，一般先用 tarjan 标记出所有割边，然后染色。

边双的缩点

把每个边双看做一个点，点的颜色作为在新的图中的编号。最终图会缩成一棵树（或森林）。

拿另一个邻接表存一下即可。

求点双

不像边双那么简单，也和割点关系不大。

过程：

当一个节点第一次被访问（dfn=0）时，该节点入栈。
若 dfn[x]<=low[y] （割点判定法则）成立：
1. 从栈顶弹出节点，直到 y 被弹出；
2. 弹出的所有节点与 x 共同构成一个 v-DCC。

由于一个节点可能被纳入多个点双，点双的记录在循环内。

void tarjan(int u)
{
	dfn[u] = low[u] = ++num;
	st.push(u);
	if (u == root && !head[u])
	{
		dcc[++cnt].push_back(u);
		return;
	}
	int flag = 0;
	for (int i = head[u]; i; i = e[i].nxt)
	{
		int v = e[i].v;
		if (!dfn[v])
		{
			tarjan(v);
			low[u] = min(low[u], low[v]);
			if (dfn[u] <= low[v])
			{
				flag++, cnt++;
				int tmp;
				do
				{
					tmp = st.top(), st.pop();
					dcc[cnt].push_back(tmp);
				} while (tmp != v);
				dcc[cnt].push_back(u);
			}
		}
		else
			low[u] = min(low[u], dfn[v]);
	}
}

点双的缩点

也复杂一些，因为一个割点可能属于多个 v-DCC。

设有 p 个割点和 t 个 v-DCC，缩点后的图将会有 p+t 个节点。把每个割点和每个 v-DCC 作为新图中的节点，并在每个割点和包含它的 v-DCC 间连边。

在此之前，要先给割点一个新的编号，从 cnt+1 开始（cnt 是 v-DCC 的个数）。

有向图的强联通分量（SCC）

强联通图：对有向图中的任意两点 x,y，既存在 x 到 y 的路径，又存在 y 到 x 的路径，这张图就是一张强联通图。

强联通分量：极大的强联通子图。

感性理解：每个强联通分量就是一个环套环形态的图，求 SCC 的过程就是尽可能找到环。

前向边：搜索树上从祖先指向后代的边。

后向边（返祖边）：搜索树上从后代指向祖先的边。

横叉边：起点终点没有祖先关系的边。

对于找环来说，前向边用处不大。后向边可以与树边构成一个环。横叉边 (x,y) 如果能从 y 走后向边回到 x 的祖宗就有用。

追溯值：这里，定义其为以下节点的时间戳的最小值。

栈内的节点。
x 的子树的节点通过一条非树边能到达的点。

求强联通分量

开一个栈，保存：

搜索树上 x 的祖先节点，这类节点的集合记作 anc(x)。
已经访问过，且存在一条路径能到 anc(x) 的节点。

当 x 第一次被访问的时候，x 入栈，初始化 low[x]=dfn[x]。

对每条出边(x,y)：

若 y 没被访问过，则其为树枝边，递归访问 y，回溯后 low[x]=min(low[x],low[y])。
若 y 被访问过了且在栈中，low[x]=min(low[x],dfn[y])。

在 x 回溯之前，若 low[x]=dfn[x]，则不断弹出节点直到 x 出栈。

弹出的节点构成一个 SCC。

这也就是强联通分量判定法则。

由于一个节点只可能被纳入一个强连通分量，强联通分量的记录在循环外。

实现

void tarjan(int u)
{
	dfn[u] = low[u] = ++num;
	st.push(u), ins[u] = 1;
	for (int i = head[u]; i; i = e[i].nxt)
	{
		int v = e[i].v;
		if (!dfn[v])
		{
			tarjan(v);
			low[u] = min(low[u], low[v]);
		}
		else if (ins[v])
		{
			low[u] = min(low[u], dfn[v]);
		}
	}
	if (dfn[u] == low[u])
	{
		cnt++;
		int tmp;
		do
		{
			tmp = st.top(), st.pop(), ins[tmp] = 0;
			scc[cnt].push_back(tmp);
		} while (u != tmp);
	}
}

Q：一个节点和它的后代构成一个强联通分量，那它的祖先如果在内，什么时候加入？

A：这种情况下，统计会发生在祖先身上。

缩点

和无向图 e-DCC 的缩点类似。

把每个 SCC 看做一个点，点的颜色作为在新的图中的编号。最终图会缩成一个 DAG。

拿另一个邻接表存一下即可。

（upd：拿另一个 vector 存更不容易混淆 ——xkj）

圆方树

圆方树：对无向图建立圆方树，在圆方树中，原来的每个点对应一个圆点，每一个点双对应一个方点，每个方点与其对应的点双包含的点连边。

长相可以借助图解：

我是图图

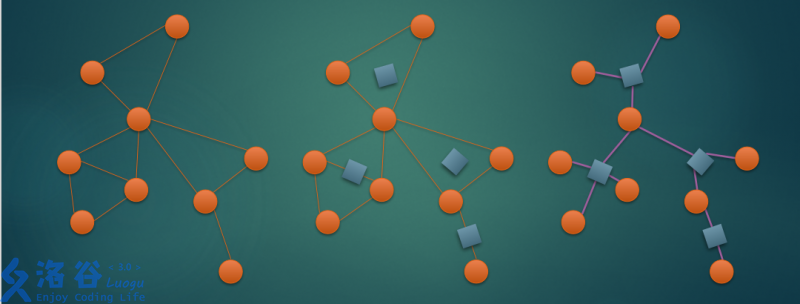
用处看题。

P4630 [APIO2018] 铁人两项

部分引用自 @Great_Influence。

可以发现，答案就是路径上可能经过的点数。

建出圆方树，统计树上路径点数。可以简单发现，如果将方点的权值标为点双大小，圆点的权值标为 \(-1\)，则某条路径上可能经过的点数就是圆方树上路径点权和。

这样做的理由是每个点双都会经过 \(1\) 次，点双中的每个点都可以作为中继点 \(c\)，但割点会在两边各统计一次，故把割点权值设为 \(-1\) 抵消重复计算。

可以统计每个点被经过多少次再乘上它的权值，直接树上差分求是 \(O(n^2)\) 的，但是可以利用简单 dfs 记录子树大小做到 \(O(n)\)。

P3225 [HNOI2012] 矿场搭建

点双缩点成圆方树。

叶子节点（只含有一个割点的点双）必须建，因为叶子节点如果不建一旦割点被爆就寄了。
非叶节点（含有两个或两个以上的割点的点双）不用建，因为即使一个割点被爆了也可以沿着另一个割点走到一个叶节点。
还有一种情况就是整个联通块都是点双（即不含割点的点双）这样我们讨论点双的大小。
- 如果只有一个点，那么这个点必须建。
- 如果有两个或两个以上的点，那么要建两个，一个被爆了还可以走另一个。

每个点的贡献就是这个点双的非割点的点的数量，乘起来就是答案。

P5058 [ZJOI2004] 嗅探器

必经点问题，考虑用圆方树解决。

一遍 dfs 求出搜索树，用 \(fa\) 记录从 \(a\) 到 \(b\) 的路径。

每次跳父亲记录最小值就可以了。

统计答案时注意舍去实际不存在的方点。

P2505 [HAOI2012] 道路

dij 写不到了（悲

好题解

波澜壮阔的一题。

最短路 \(\rightarrow\) 最短路图

最短路图：源点到其他所有点的最短路的并，是一张 DAG。

五步走：

跑 dij 跑出最短路图。
- 如果一条边 \((u,v)\) 满足 \(dis_v=dis_u+w(u,v)\)，则其在最短路图上。
在最短路图上拓扑排序。
按照拓扑序，求出任意一个点 \(u\)，\(S\) 到 \(u\) 的最短路径的数目 \(cnt_1 [u]\)。很显然，\(cnt_1[S]=1\)，如果最短路图上存在边 \(u→v\)，则 \(cnt_1[v]+=cnt_1[u]\)。
再按照拓扑序的逆序，求出任意一个点 \(u\)，在最短路图上以 \(u\) 为起点的路径条数 \(cnt_2[u]\)。容易得到，如果先把每个点的 \(cnt_2\) 设为 \(1\)（路径中只包含 \(u\)），那么如果最短路图上存在边 \(u→v\)，则 \(cnt_2[u]+=cnt_2[v]\)。
统计贡献。对于在最短路图上的一条边 \(u→v\)，贡献为 \(cnt_1[v] \times cnt_1[u]\)，即进入起点的方案数和出终点后的方案数。

P2783 有机化学之神偶尔会做作弊

边双缩点 + lca 数距离。

记得判断重边和自环，没保证就是有，要特殊考虑。

有些开不下的东西就用 map 存。

P4645 [COCI2006-2007#3] BICIKLI

数路径条数，这个要分讨。

若 \(1\) 和 \(2\) 不联通，答案自然为 \(0\)。

如果路径上可以经过一个 SCC，那在里面绕多少圈都可以，答案 inf。

怎么判断一个 SCC 是不是在 \(1\) 到 \(2\) 的路径上呢？我们可以正着从 \(1\) DFS 一遍，再建反图从 \(2\) DFS 一遍，这样两遍都搜到的 SCC 就是路径上的了。

概括地说，有向图上从 \(s\) 到 \(t\) 的经过点，就是从 \(s\) 出发所能经过的所有点与从 \(t\) 出发在反图上所能经过的所有点的交集。这些点都满足从 \(s\) 出发能走到，从这个点出发能走到 \(t\)。

如果前两条都不满足，就把路径上的 SCC 拓扑排序，跑 DP 即可。

P2746 [USACO5.3] 校园网Network of Schools

首先肯定缩点，SCC 内的点都可以互相转发，接下来的图是缩点以后的。

第一问：每个入度为 \(0\) 的点都必须要发一个，每个入度不为 \(0\) 的点都可以溯流而上找到一个入度为 \(0\) 的点，故只需要给每个入度为 \(0\) 的点发一个就可以了。

第二问：问题是最少加几条边可以把整张图加成一个强联通图。

一个入度为 \(0\) 的点必须要加一条入边。一个出度为 \(0\) 的点必须要加一条出边。我们让每个出度为 \(0\) 的点都连向一个入度为 \(0\) 的点，这样就可以保证每个点均有出度入度，这是必要的。

为什么这充分呢？第一篇题解有详细证明，与二分图相关，构造 SCC。

其实画几个图就可以初步判断了。

题解

P5008 [yLOI2018] 锦鲤抄

贪心地，肯定想获得尽可能大的 \(k\) 个（如果有）。

先缩点，发现按拓扑序的倒序来选点的话，后选的点一定与先选的点无关。因为只删掉指向后面的出边。

我们把所有能选的点找出来，然后选前 \(k\) 大的就可以了。

每个 SCC 内部不一定都能选，要分讨：

SCC 内有自环：

可以全选，最后选自环的。
SCC 内没有自环，但 SCC 有入度：

可以全选，最后选有 SCC 外入度的。
SCC 内没有自环，也没有入度：

必须要留下一个不能选，我们选择贪心地留下最小的一个。

全部丢进一个 set 里面就可以了。

P3119 [USACO15JAN] Grass Cownoisseur G

最喜欢的一集。

题意是求有向图的最大环，但是可以在环上“逆行”一次。

照例缩点，一个 SCC 内的点都可以互相通达。对新图的每条边考虑，我们逆行这条边，答案就是（这条边起点到 \(1\) 号点的距离 + \(1\) 号点到这条边终点的距离）。

实现上，处理出 \(1\) 到其他点的距离和其他点到 \(1\) 的距离，这可以用最短路实现，但显然在 DAG 上更优秀的方案是拓扑排序后 DP。

P2403 [SDOI2010] 所驼门王的宝藏

精妙的一题。

如果能把所有边连出来，那就是一个缩点 + DAG 最长路的套路题，但是这题的难点就在连边上。

考虑给每行、每列都设一个虚点，横天门就连边指向这一行的虚点，同时每行的虚点连边指向这一行的所有节点。这样横天门通过中继虚点可以抵达这一行的所有点。纵列同理。

任意门就暴力连边即可，把所有关键点存下来，要找的时候按按横纵坐标二分查找。

这道题卡空间，需要根据每行每列的使用情况动态开虚点空间。

标签：Tarjan,连通性,int,割点,SCC,dfn,low,节点
From： https://www.cnblogs.com/tai-chi/p/18340970