首页 > 其他分享 >图论连通性

图论连通性

时间：2024-07-15 20:51:42浏览次数：11  
标签：图论 连通性 int top cnt st dfn low

【学习笔记】图论连通性

啊啊啊啊啊!

先引用一篇犇的：）））

缩点

弱连通：

对于有向图中两点 \(x\) 和 \(y\)，它们在所有边为无向时存在一个环使它们相连。

强连通：

对于有向图中两点 \(x\) 和 \(y\)，存在一个环使它们相连。

强连通子图：

对于有向图 \(G = (V, E)\)，如果对于一个 \(V\) 的子集 \(V_0\) 满足，\({\forall x, y \in V_0}\)，\(x\) 和 \(y\) 均满足强连通，则称 \(V_0\) 为一个强连通子图。

强连通分量（SCC）：

极大的强连通子图。（一个图中可以有多个）

  • 极大的的含义：对于一个强连通子图 \(V_0\)，满足 \(\forall V_0 \subset V_1\)，且 \(V_1\) 都不是强连通子图。

Tarjan 算法

一些定义：

  • 在 dfs 过程中遍历的边称为树边，未遍历的边称为非树边。

  • \(dfn_x\) 表示图中 \(x\) 号节点在 dfs 算法中是第 \(x\) 个遍历到的。

  • \(low_x\) 表示 \(x\) 号节点经过若干条树边后再经过至多一条满足条件的非树边能到达的 \(dfn\) 最小的点的值。

实现方法：

  • 算出 \(dfn_x\) 并初始化 \(low_x\)：可以全局记录一个时间戳 \(T\)，并使 dfn[x] = low[x] = ++T。

  • 枚举 \(x\) 的所有出边指向的点 \(y\)。有两种情况：

  1. \(y\) 还没有被遍历过。可以直接调用 dfs(y)，因为该边是树边，所以直接更新 low[x] = min(low[x], low[y])。

  2. \(y\) 已经被遍历过了。如果 \(y\) 和 \(x\) 在同一个 SCC（\(y\) 存在到 \(x\) 的路径），则更新 low[x] = min(low[x], dfn[y])。

    2.1. 如何知道是否在一个 SCC 里呢？（判断横叉边）

    我们可以考虑开一个栈，在进入 dfs(x) 是将 \(x\) 入栈，并在找到 \(x\) 所在的 SCC 的所有点后将 \(x\) 弹出栈。

    所以，此时如果 \(y\) 在这个栈中，则证明 \(y\) 到 \(x\) 存在路径，否则不存在。因此如果 \(y\) 此时在栈中则更新 low[x] = min(low[x], dfn[y])。否则不用更新。

  • 结束 dfs 时，判断 \(x\) 是否为其所在 SCC 内 \(dfn\) 最小的点。

  1. 如果 \(dfn_x = low_x\)，则 \(x\) 是 \(dfn\) 最小的点。此时将栈中 \(x\) 及以上的元素弹出。这些元素即是跟 \(x\) 处于同一 SCC 的点。

  2. 否则 \(x\) 不是 \(dfn\) 最小的点，直接结束 dfs。

代码如下：

vector<int> g[N];
vector<int> scc[N];
int w[N], dfn[N], low[N], T, cnt;
int st[N], top;
bool ins[N];

void tarjan(int u){
    dfn[u] = low[u] = ++T;
    st[++top] = u, ins[u] = 1;
    for(int v : g[u]){
        if(!dfn[v]){
            tarjan(v);
            low[u] = min(low[u], low[v]);
        } else if(ins[v]){
            low[u] = min(low[u], dfn[v]);
        }
    }
    if(dfn[u] == low[u]){
        cnt++;
        while(st[top] != u){
            scc[cnt].push_back(st[top]);
            ins[st[top--]] = 0;
        }
        scc[cnt].push_back(st[top]);
        ins[st[top--]] = 0;
    }
}

一个 SCC 实际上就对应着一个可以单点经过多次的非简单环，那么如果我们把 SCC 缩成一个点，也就意味着把一个一般有向图变成了 DAG。

由于 Tarjan 算法以及后续的缩点只需要遍历一次图，所以算法的总时间复杂度为 \(O(n+m)\)。

然后 DAG 上可以用拓扑排序 DP 来解决问题。

trick：统计出来的 SCC 里 \(cnt\) 由大到小就是拓扑序。

P3387 【模板】缩点

板子。注意 trick 运用方式。

#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 1e4+5;

int n, m;
vector<int> g[N];
vector<int> scc[N]; // scc 里 cnt 由大到小就是拓扑序
vector<int> gn[N]; // scc 新图
int w[N], dis[N], dfn[N], low[N], T, cnt, ans;
int st[N], top;
bool ins[N];
int inscc[N], dp[N];

void tarjan(int u){
    dfn[u] = low[u] = ++T;
    st[++top] = u, ins[u] = 1;
    for(int v : g[u]){
        if(!dfn[v]){
            tarjan(v);
            low[u] = min(low[u], low[v]);
        } else if(ins[v]){
            low[u] = min(low[u], dfn[v]);
        }
    }
    if(dfn[u] == low[u]){
        cnt++;
        while(st[top] != u){
            scc[cnt].push_back(st[top]);
            inscc[st[top]] = cnt;
            dis[cnt] += w[st[top]];
            ins[st[top--]] = 0;
        }
        scc[cnt].push_back(st[top]);
        inscc[st[top]] = cnt;
        dis[cnt] += w[st[top]];
        ins[st[top--]] = 0;
    }
}


int main(){
    ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
    cin>>n>>m;
    for(int i=1; i<=n; i++)
        cin>>w[i];
    for(int i=1; i<=m; i++){
        int u, v; cin>>u>>v;
        g[u].push_back(v);
    }
    for(int i=1; i<=n; i++)
        if(!dfn[i]) tarjan(i);
    for(int i=1; i<=n; i++){
        for(int j : g[i]){
            if(inscc[i] != inscc[j])
                gn[inscc[i]].push_back(inscc[j]);
        }
    }
    // dp
    for(int i=cnt; i>=1; i--){  
        dp[i] = max(dp[i], dis[i]);
        for(int j : gn[i]){
            dp[j] = max(dp[j], dp[i] + dis[j]);
        }
        ans = max(dp[i], ans);
    }
    cout<<ans;
    return 0;
}

割点与割边

割点：

将某点从图中去掉后，得到了一个非连通图，则称这个点是割点。

割边：

将某边从图中去掉后，得到了一个非连通图，则称这条边是割边。

dfs 树：

对于一个无向图，通过 dfs 算法得到的一颗生成树。

  • 在 dfs 过程中遍历的边称为树边，未遍历的边称为环边。
  • 所有的环边一定是返祖边。
  • 没有横叉边。

一些定义：

  • \(dfn_x\) 表示图中 \(x\) 号节点在 dfs 算法中是第 \(x\) 个遍历到的。

  • \(low_x\) 表示 \(x\) dfs 树的子树内，通过环边能回到的 \(dfn\) 最小的点。

实现方法（如何判断一个点 \(x\) 是割点）：

  • 若 \(x\) 是 dfs 树的根，\(x\) 是割点当且仅当 \(x\) 有不少于两个儿子。

  • 否则，\(x\) 是割点当且仅当存在一个 \(x\) dfs 树的儿子 \(y\) 使得 \(low_y \ge dfn_x\)。

    证明：若删去 \(x\)，则 \(y\) 子树内没有向 \(x\) 祖先以及其它子树连接的边，故 \(y\) 子树与其它点会形成两个连通块。故 \(x\) 是割点。

实现方法（如何判断边 \((x, y)\) 是割边）：

  • 若 \((x, y)\) 是环边，则该边一定不是割边，因为删除该边之后生成树不受影响。

  • 若 \((x, y)\) 是树边，假设 \(x\) 是 \(y\) 的父亲，则该边是割边当且仅当 \(low_y > dfn_x\)。

    证明：若 \(low_y > dfn_x\)，则删除该边后，\(y\) 子树内与 \(y\) 子树外会分成两个连通块，故该边为割边。否则，在删除边后 \(y\) 子树内与 \(y\) 子树外仍然连通，故该边不是割边。

点双与边双

割点决定点双，割边决定边双。

点双连通图：

如果一个无向图不存在割点，则称该图是一个点双连通图。

等价定义：图中任意两点都存在两条除了起点终点外点不相交的路径。

边双连通图：

如果一个无向图不存在割边，则称该图是一个边双连通图。

等价定义：图中任意两点都存在两条边不相交的路径。

点双连通分量：

极大的点双连通子图。

边双连通分量：

极大的边双连通子图。

思路：

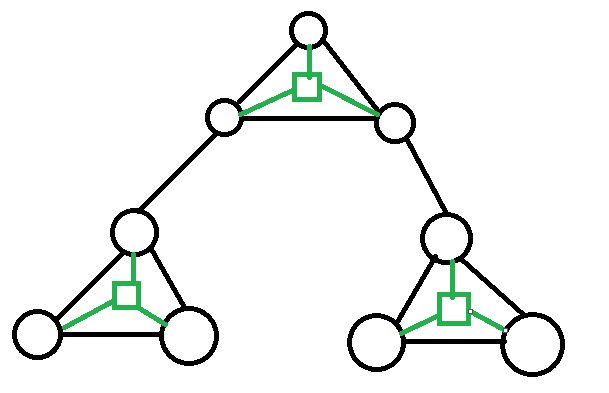
边双连通分量缩点后得到的图为树，而点双连通分量“缩点”后得到的图为圆方树。

圆方树的含义是用圆点表示原图上的点，方点（新建点）表示不同的点双。（再把原点双的边去掉就得到了一棵树）

P8436 【模板】边双连通分量

板子。注意重边处理方式。

#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 5e5+5;

int n, m;
vector<int> g[N];
vector<int> bs[N];
int dfn[N], low[N], T;
int st[N], top, cnt;
bool vis[N]; // 是否被遍历过

void tarjan(int u, int fa, int id){
    dfn[u] = low[u] = ++T;
    st[++top] = u; vis[u] = 1;
    for(int v : g[u]){
        if(v == fa && id == 0){
            id = 1;
            continue;
            // 处理重边
        }
        if(!vis[v]){
            tarjan(v, u, 0);
            low[u] = min(low[u], low[v]);
        } else{
            low[u] = min(low[u], dfn[v]);
        }
    }
    if(dfn[u] == low[u]){
        cnt++;
        while(st[top] != u){
            bs[cnt].push_back(st[top]);
            top--;
        }
        bs[cnt].push_back(st[top]);
        top--;
    }
}

int main(){
    ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
    cin>>n>>m;
    for(int i=1; i<=m; i++){
        int u, v; cin>>u>>v;
        g[u].push_back(v);
        g[v].push_back(u);
    }
    for(int i=1; i<=n; i++)
        if(!vis[i]) tarjan(i, 0, 0);
    cout<<cnt<<"\n";
    for(int i=1; i<=cnt; i++){
        cout<<bs[i].size()<<" ";
        for(int j : bs[i]) cout<<j<<" ";
        cout<<"\n";
    }
    return 0;
}

P8435 【模板】点双连通分量

板子。

#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 5e5+5;

int n, m;
vector<int> g[N];
vector<int> ds[N];
int dfn[N], low[N], T;
int st[N], top, cnt;
bool vis[N]; // 是否被遍历过

void tarjan(int u, int fa){
    dfn[u] = low[u] = ++T;
    st[++top] = u; vis[u] = 1;
    int son = 0;
    for(int v : g[u]){
        if(v == fa) continue;
        if(!vis[v]){
            son++;
            tarjan(v, u);
            low[u] = min(low[u], low[v]);
            if(low[v] >= dfn[u]){
                cnt++;
                while(st[top+1] != v){
                    ds[cnt].push_back(st[top]);
                    top--;
                }
                ds[cnt].push_back(u);
            }
        } else{
            low[u] = min(low[u], dfn[v]);
        }
    }
    if(fa == 0 && son == 0) ds[++cnt].push_back(u); // 孤立点判定
}

int main(){
    ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
    cin>>n>>m;
    for(int i=1; i<=m; i++){
        int u, v; cin>>u>>v;
        g[u].push_back(v);
        g[v].push_back(u);
    }
    for(int i=1; i<=n; i++)
        if(!vis[i]) tarjan(i, 0);
    cout<<cnt<<"\n";
    for(int i=1; i<=cnt; i++){
        cout<<ds[i].size()<<" ";
        for(int j : ds[i]) cout<<j<<" ";
        cout<<"\n";
    }
    return 0;
}

P2860 [USACO06JAN] Redundant Paths G

由题意很自然想到可以边双缩点，然后建新图并找到叶子节点的个数。

答案为 \(\lfloor \frac{s+1}{2} \rfloor\)（\(s\) 为叶子节点数）。

转证明。

口胡一下另一种：将度数为 2 的点缩了之后，每次连距离最长的两个叶子节点即可。

#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 5e3+5;

int n, m;
vector<int> g[N];
vector<int> bs[N];
int dfn[N], low[N], inbs[N], T;
int st[N], top, cnt, leaf;
bool vis[N]; // 是否被遍历过
int ind[N];

void tarjan(int u, int fa, int id){
    dfn[u] = low[u] = ++T;
    st[++top] = u; vis[u] = 1;
    for(int v : g[u]){
        if(v == fa && id == 0){
            id = 1;
            continue;
            // 处理重边
        }
        if(!vis[v]){
            tarjan(v, u, 0);
            low[u] = min(low[u], low[v]);
        } else{
            low[u] = min(low[u], dfn[v]);
        }
    }
    if(dfn[u] == low[u]){
        cnt++;
        while(st[top] != u){
            bs[cnt].push_back(st[top]);
            inbs[st[top--]] = cnt;
        }
        bs[cnt].push_back(st[top]);
        inbs[st[top--]] = cnt;
    }
}

int main(){
    ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
    cin>>n>>m;
    for(int i=1; i<=m; i++){
        int u, v; cin>>u>>v;
        g[u].push_back(v);
        g[v].push_back(u);
    }
    for(int i=1; i<=n; i++)
        if(!vis[i]) tarjan(i, 0, 0);
    for(int i=1; i<=n; i++){
        for(int j : g[i]){
            if(inbs[i] != inbs[j]){
                ind[inbs[j]]++;
                // 每个点都会被遍历到一次，因为之前已经连的是无向边，所以统计一个就行。
            }
        }
    }
    for(int i=1; i<=cnt; i++)
        if(ind[i] == 1) leaf++;
    cout<<(leaf+1)/2;
    return 0;
}

标签：图论,连通性,int,top,cnt,st,dfn,low
From： https://www.cnblogs.com/FlyPancake/p/18303948

相关文章

  • 图论_杨宁远
    图论_杨宁远A-01Balanced差分约束本质求得最大解题面考虑构造一个长度为\(N\)的字符串s，由0和1组成，其中\(s\)必须满足\(M\)个条件。第\(i\)个条件由整数\(L_i​\)和\(R_i​（1≤L_i​<R_i​≤N）\)表示。这意味着在字符串\(s\)的第\(L_i\)​个字符和第\(R_i​\)个......
  • 无向图的连通性（割点与割边）
    割点与割边 割点的求解方法  割点详解 板题：https://www.luogu.com.cn/problem/P3388  第1题   割点 查看测评数据信息给出一个n个点，m条边的无向图，求图的割点。输入格式 第一行输入两个正整数n,m。下面m行每行输入两个正整数x,y表示x到y有一......
  • 动态图连通性笔记
    首先离线的话有几种方法：线段树分治动态维护最大生成树：边的权值为他的（下一次）删除时间，加边正常做，询问时问路径最小值是否小于当前时刻.动态图连通性Holm-deLichtenberg-Thorup(HLT)暴力：维护生成森林，若删树边则暴力找另一条边能替代这条树边.思想：给每条边赋一个“不重......
  • 【代码随想录——图论——小岛问题】
    1.水流问题使用两个visited数组即可。1.1DFS版packagemainimport"fmt"vardirection=[][]int{{0,1},{0,-1},{1,0},{-1,0}}funcmain(){ varM,Nint fmt.Scanln(&N,&M) sea:=make([][]int,N) one_visited:=make([][]bool,N) two_visi......
  • 【代码随想录|第十一章 图论part01 | 797.所有可能的路径 】
    代码随想录|第十一章图论part01|图论理论基础，797.所有可能的路径，广搜理论基础一、图论理论基础1.图的基本概念2.图的构造1）邻接矩阵2）邻接表3.图的遍历方式4.深度优先搜索理论基础二、797.所有可能的路径1.核心代码2.问题三、广搜理论基础总结python一、图论理......
  • 二十个基于 Python 的 NetworkX 图论算法库入门应用实例
    前言大家好，最近我在美丽的重庆度过了一段美好的学习时光。重庆以其独特的山城地貌和美食闻名，而在火锅和享受美食之余，这里的项目学习激发了我对图论的兴趣。图论是一门既古老又新兴的学科，它在计算机科学、网络分析、社会网络、物流优化等领域有着广泛的应用。而Python的......
  • 数据融合工具（6）线要素网络连通性分组计算
            出行，一直在使用导航辅助我们从起点奔赴终点，或许我们会有过这样的思考？导航路线规划是怎么实现的？        ……        我们先掰扯掰扯……一、导航路线规划是如何实现的？        导航路线规划是一种复杂的算法和技术，它用于确定......
  • [学习笔记] 长链剖分 - 图论
    长链剖分字面意思，不同于重链剖分，每次选取最长的树链进行剖分，直到剖完为止。其原理和重链剖分相似。建议学习长链剖分前，先学习重链剖分。重链剖分能做的，长链剖分都能做（当然不包括找重儿子），长链剖分还能以\(O(nlogn)-O(1)\)的优秀复杂度找到\(k\)级祖先（当前节点的第\(k\)个......
  • 图论
    点双连通分量#include<bits/stdc++.h>#definesz(a)int((a).size())#defineFOR(i,l,r)for(inti=l;i<=r;i++)#defineROF(i,r,l)for(inti=r;i>=l;i--)#definelllonglong#definexfirst#defineysecond#definepipair<int,int&g......
  • 代码随想录算法训练营第56天 | 图论理论基础 、深搜理论基础、98. 所有可达路径、广
    图论理论基础今天主要是理论大家可以在看图论理论基础的时候，很多内容看不懂，例如也不知道看完之后还是不知道邻接矩阵，邻接表怎么用，别着急。理论基础大家先对各个概念有个印象就好，后面在刷题的过程中，每个知识点都会得到巩固。https://www.programmercarl.com/kamacoder/图......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99