图论_杨宁远
A - 01 Balanced
差分约束本质求得最大解
题面
考虑构造一个长度为\(N\)的字符串s,由0和1组成,其中 \(s\) 必须满足 \(M\) 个条件。 第 \(i\) 个条件由整数\(L_i\)和\(R_i(1≤L_i<R_i≤N)\)表示。 这意味着在字符串 \(s\) 的第 \(L_i\) 个字符和第 \(R_i\) 个字符(包括)之间应该有相等数量的0和1。
解法
【题解】AGC056C 差分约束 思维 建模 - 洛谷专栏 (luogu.com.cn)
方法
-
差分约束本质找到最大解
原因:其在最强的限制 \(dis\le val\) 取等,
D - 最大XOR和路径
一点思路都没有,应该去看样例
题面
考虑一个边权为非负整数的无向连通图,节点编号为 \(1\) 到 \(N\),试求出一条从 \(1\) 号节点到 \(N\) 号节点的路径,使得路径上经过的边的权值的异或和最大。
解法
假设一开始有一条从 \(1\) 号节点到 \(N\) 号节点的链。
假设\(k\)是连接这条链和某个环的某条路径,那么显然,链和环都将走过一遍,而这条路径k会被走过两遍(从链到环一遍,从环到链一遍)。根据我们上面的推论,k对答案的贡献是0。于是我们发现,我们根本就没有必要算出这条路径\(k\)!(反正贡献是0)
于是我们枚举所有环,将环上异或和扔进线性基,然后用这条链作为初值,求线性基与这条链的最大异或和。
后说一下怎么选最开始的这条链,其实它可以随便选。我们考虑以下这种情况:
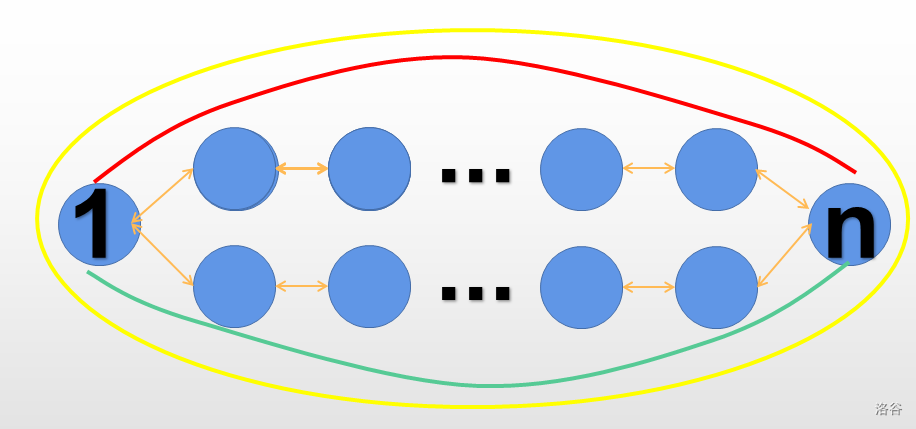
假设路径A比路径B优秀一些,而我们最开始选择了路径B。显然,A与B共同构成了一个环。如果我们发现路径A要优秀一些,那么我们用B异或上这个大环,就会得到我们想要的A!
方法
-
线性基
-
模拟过程
模拟样例的过程,研究答案的组成
E - Edges in MST
题面
给出一个 \(n\) 个点 \(m\) 条边的无向图,保证连通。
每条边有正整数边权,统计每条边的情况属于:
- "any" 这条边在每种最小生成树上
- "at least one" 这条边至少在某种最小生成树上
- "none" 这条边不在任何最小生成树上
\(2\le n\le 10^5,n-1\le m\le \min(10^5,\dfrac{n(n-1)}2)\)
解法
考虑 Kruskal 的加边过程,可以将边权相同的边统一考虑。
-
如果一条边连接的两个连通块在之前已经被联通了,则为 none
-
如果他是桥,则为 any
-
否则为 at lest one
处理完后将那些可以每条边连接的两个连通块合并
方法
-
Tarjan连通性
-
模拟过程
模拟Kruskal的算法过程
F - Tourists
只向上考虑父亲,减少修改复杂度
G - Too Many Constraints
将取值范围为 \(k\) 的值变为 \(k\) 个0/1变量
题面
求你建立一个数组 \(a\), 由 \(n\) 个整数组成, 每个元素的范围应为 \(1\) 到 \(k\).
数组应该是非递减的(\(\forall i\in[1,n-1],a_i≤a_{i+1}\) ).
您还会得到额外的约束条件。每个约束都是以下三种类型之一:
- \(1 i x : ai\) 不应等于 \(x\) ;
- \(2 i j x : ai+aj\) 应小于或等于 \(x\) ;
- \(3\ i j x : ai+aj\) 应大于或等于 \(x\) 。
建立满足所有约束条件的非递减数组,或者报告不存在这样的数组。
解法

方法
-
01变量思想
-
k-sat拆为2-sat
设01变量 \([a\ge x]\)
本质为“若……则……”的偏序关系
-
枚举
H - 序列
找到若则关系
题面
有一个长度为 \(n\) 的序列 \(a_1,a_2,…,a_n\),序列里的每个元素都是 \([1,10^9]\) 内的正整数。
现在已知了 \(m\) 条信息,每条信息形如 \(i,j,k,x\),表示 \({a_i,a_j,a_k}\) 的中位数为 \(x\)
请构造一个满足条件的序列。
\(1\le n\le 10^5\)
解法
对于 \(i,j,k\) 中任意两个数 \(p,q\),应该满足 \([a_p<x]\implies[a_q\ge x],[a_p>x]\implies [a_q\le x]\) 以及他们的逆否命题
直接建边跑 2-sat 即可。
注:\([a_p<x]\) 可以表示为 \([a_p\le x-1]\)
方法
- 2-sat
I - Flip and Reverse
相邻状态中的变化关系
题面
给定 01 字符串 \(s\),现在你能进行若干次操作,对于每一次操作:
- 选择字符串 \(s\) 的连续的一段子串,要求这段子串必须包含同样数量的字符
0与1。 - 把该子串的所有字符转换,即所有字符
0换为1,字符1换为0。 - 把选中的子串反转。
求经过若干次操作后字典序最小的字符串。
多测。
\(1\le T\le 10^5,1\le \sum|s|\le 10^5\)
解法
令 \(a_i=a_{i-1}+[s_i=1]-[s_i=0]\)
于是若区间 \([l,r]\) 中 01 数量相等,则一定有 \(a_r=a_{l-1}\),即回到之前的状态,整个过程构成了一个环。可以发现(可以数形结合画图观察)每次操作其实是把一个环反着走,于是问题变成了有一个无向图,从 \(0\) 出发,要使每条边恰好经过一次,求字典序最小的走法,直接构造即可。
方法
-
偏序关系
从一个状态变化到另一种状态是一种偏序关系
-
数形结合
不然很难发现操作是在干嘛
J - Red-Blue Graph
状态与答案的关系
题面
给定一张 \(n(2\le n\le 58)\) 个点的图,除了 \(n\) 号点外的每个点都有两条出边,分别被染成红色和蓝色,每个点的两条出边在任意时刻均有且仅有一条是活跃的,保证 \(n\) 从任意一个点出发可达。
一开始,所有蓝边都是活跃的,你在 \(1\) 号点,每秒将会依次发生以下事件:
-
你所处的点的两条出边活跃性交换,即活跃的边变成不活跃的,不活跃的边变成活跃的。
-
你走到活跃的边所指向的点。
如果走到 \(n\) 号点则停止走动。
将会给出 \(q(1≤q≤5000) \)组询问,每组询问将会给出一个正整数 \(v(1≤v<n)\) 和长为 \(n−1\) 的由 R 和 B 组成字符串 \(s\),表示一个你所在的点和每个点的活跃的出边的颜色的状态,你需要找出这个状态首次出现是在第几秒末,如果不存在这个状态则回答 -1。
注意每秒中间仅进行了状态翻转操作后尚进行移动操作时出现的状态并不算“出现是在第几秒末”中的“出现”。
解法
注意到每个时间与一个形如 \(\{所在点,活跃边颜色状态\}\) 的状态时一一对应的,于是我们可以从询问找到可能的对应时间点的性质。
当一个点的活跃边状态确定的时候,我们可以知道经过这个点的次数的奇偶性。
对于状态 \(\{p,c_1c_2\cdots c_{n-1}\}\) ,假设点 \(i\) 走了蓝边 \(x_i\) 次。则走了红边 \(x_i+[s_i=R]\) 次,由于出入次数平衡,我们可以建立等式(注意需要特判 \(p\) 节点与 \(1\) 节点),接着高斯消元,复杂度为 \(\mathcal O(qn^3)\)。
由于一个线性方程组可以被表示为 \(A\vec x=\vec b\),根据上面的分析可知,不同的状态只会修改 \(\vec b\),而不会修改系数矩阵 \(A\), 因为 \(A\) 一定是满秩矩阵,我们可以求出 \(A\) 的逆元 \(A^{-1}\),得到\(\vec x=A^{-1}\vec b\),复杂度为 \(\mathcal O(n^3+qn^2)\)。
最后判断无解,当一个状态有解当且仅当满足以下两个性质:
-
\(\vec x\) 有非负整数解
-
对于 \(2x_i+[s_i=R]\) 不为 \(0\) 的每一个点,都能通过当前的状态中活跃的激活边到达,必要性显然,充分性可以归纳。
求逆元的操作迫使我们加上取模以保证精度,具体可以找两个大于 \(10^{18}\) 次方的不同质数,如果得到 \(\vec x_i\) 值相同,则几乎一定为非负整数解。
方法
-
方程思想
建立元素之间的等量关系
-
归纳
-
高斯消元,系数矩阵不变时,先矩阵求逆。
O - Bricks
题面
有一个 \(n×m\) 网格,每个单元格要么是黑色要么是白色。用长或宽为一的矩形覆盖所有黑色单元格,并且没有两块砖重叠,求最少需要几块砖
\(1\le n,m\le 200\)
解法
有一个朴素的思路是将各种可能的砖头都建一个点,接着建图跑最大流,但这样会建立 \(\mathcal O(n^2m+nm^2)\) 个点,跑最大流会超时。
我们可以关心相邻的位置,查看相邻的位置能否由一个砖块覆盖,这样做的意义在于,就算是有一个很长的砖块,也一定因为两个子部分内部可以合并,加上这两个子部分可以合并为一个。容易发现,合并两个位置就会将答案减一,那么我们应该让选择的合并尽量的多。但有一个限制是,一个点不能在上下合并的同时左右合并。
那么可以将上下左右的限制连无向边,最后成为一个二分图,那么答案就为 \(总黑点数-二分图最大独立集\)
方法
-
无向关系
-
由单元及整体的思想
小的合并成大的
Q - 切糕
题面
有一个 \(n\times m\) 的矩阵 \(a\in[1,R]\),每个位置及这个位置的数合起来有一个权值 \(v(i,j,a_{i,j})\) 。现在给出这个所有的权值 \(v\) ,求满足相邻位置(上下左右)的值之差 \(\le D\) 这一限制的情况下,权值和最小是多少,即使得 \(\sum_{x,y}v(x,y,a_{x,y})\) 最小。
\(1\le n,m,R\le 40,0\le D\le R\)
解法
考虑建立最小割模型。
对于每个位置,选择一个权值可以看作将这条边割掉,所以应该建立一条链,即(图中表示两个位置)
值之差 \(\le D\) ,可以看作当前位置值为 \(\ge k\),则相邻位置的值应该 \(\ge k-D\),于是连边(图中 \(D=2\))

跑最小割即可。
方法
-
最小割
最小割中,串联表示选择一个,并联表示选择同时选择,无穷大的边表示限制——若p则q,p,q不一定是布尔变量,但有时不可以使用。
串联 并联
T - 太空飞行计划问题
题面
有m个实验,每个实验只可以进行一次,但会获得相应的奖金,有n个仪器,每个实验都需要一定的仪器,每个仪器可以运用于多个实验,但需要一定的价值,问奖金与代价的差的最大值是多少?
解法
这是一个经典的网络流问题,如果一个点被选择了则后继必须被选择,那么称该图是 闭合的,因此该问题叫做最大权闭合子图问题。可以使用最小割解决。
具体的建图方法为:
源点向所有正权点连结一条容量为权值的边
保留原图中所有的边,容量为正无穷
所有负权点向汇点连结一条容量为权值绝对值的边
则原图的最大权闭合子图的点权和即为所有正权点权值之和减去建出的网络流图的最小割。
考虑证明:
先证明得到的子图是闭合的:
首先考虑由于求得是最小割,一个点要么和 s 相连,要么和 t 相连,否则一定割掉它向 s 或 t 的一条边是没有意义的,因为割掉该边不会改变图的不连通性,最小割不会割掉它。
由于原图中的边全部是正无穷,最小割只会割掉源点和正权点之间或负权点和汇点之间的边。
考虑如果选择了正权点 u,为了保证 s−t 不连通,必须割掉 u 所有后继中的负权点。这证明了如果选择了一个正权点那么所有的后继负权点都会被选择。
如果选择了正权点 u,设 v 是 u 的后继且 v 的的权值为正,由于没有割掉 u,通过 u−v 之间的正无穷边总能使得 s−v 联通,于是割掉 s−v 的边是没有意义的,最小割不会割掉这条边,这证明了如果选择了一个正权点那么该点的所有后继正权点都会被选择。
点权为 0 的情况同理。
考虑事实上选择的闭合子图的过程是不可能从一个负权点开始的,因为去掉这个负权点直接选择它的后继显然优于选择该点。于是只考虑选择正权点就可以包括所有的情况。证毕。
再证明得到的是最大权子图:
考虑如果 i 与 s 联通,那么选择 i,否则不选择 i。所以最小割割掉的权值和是 不被选择的正权点权值和 + 被选择的负权点的权值的绝对值和 ,即 最小割 = min{没被选择的正权点权值和 + 被选择的负权点的权值的绝对值和}
于是
\(最大权闭合子图的权值和 = max{被选择的点权和} \\= 正点权和−min{没被选择的正权点之和 + 被选择的负权点绝对值和} \\= 正点权和−最小割\)
证毕。
于是本题只需要按照上述方法建图即可。输出方案只需要输出与 s 联通的点。
方法
- 最小割
V - Dominance
题面
给出一个宽为 \(W\),高为 \(H\) 的矩形 。
在它上面有两种点,共 \(n\) 个, \(black\) 及 \(white\)。 每个点都有自己的辐射范围。对于其它的点如果它受到白点的辐射多于黑色的,则为白点,反之亦然,如果相同的话则中立。
现给出白点及黑色的坐标及各自的辐射范围,问最后白色点一共有多少个,黑色点共有多少个 。
\(1\le W,H\le 10^9,0\le n\le 3\times 10^3\)
解法
[CEOI2008] Dominance-题解 - 洛谷专栏 (luogu.com.cn)
标签:10,图论,le,题面,最小,选择,权值,宁远 From: https://www.cnblogs.com/lupengheyyds/p/18303126