标签：总结 sz 图论 cn luogu www https com

重链剖分

树上修改，查询路径信息之类的 最多经过logn个轻边，这样可以更好地划分

注意点:

修改边权可以转化到点权上面：注意lca的位置不要修改，应该是update(id[y]+1,id[x])

例题：

轻重边：

https://www.luogu.com.cn/problem/P7735

判断是不是重边，信息转化到点上面，边两端的颜色相同就是重（这样好在图上修改）

树上维护颜色段数：

https://www.luogu.com.cn/problem/P2486

维护每个区间左右的颜色，以及每一个段的不同颜色个数，记录左右端点的颜色

某一条路径上，颜色为ci的有多少，可以用动态开点每个颜色开一个线段树：
https://www.luogu.com.cn/problem/P5838

P4211 [LNOI2014] LCA

经典套路：求一个点和多个点的lca的深度和，可以转化成:

比如z和l~r中每个点的lca的深度和：

l~r这些点到根的路径全部+1,然后查询z到根路径上的点权和

对于多个区间的时候：

除了用主席树：把每个右端点当做版本，
如果可以离线，并且满足区间可减性：可以把区间拆成左右端点，然后排序以后询问

P3676 小清新数据结构题

这道题可以以1为根的时候的值作为基准，推式子，退出来以x为根的时候的答案会增大多少，以及修改x权值的时候以1为根的值会增大多少

假设all是所有点权的和

对于第一个问题：我们发现只有x->root路径上的点的sz[u]会变假设从root->x的点是： a1,a2...an

会变成ai的贡献是(all-sz[ai+1])^2(这里的sz[u]是以1为根的)

所以会增大的就是dep[x]all^2 - all ^ 2 - 2all*(sz[a2]+sz[a3]+...+sz[adep])

对于第二个:就是sigema :(sz[u] + d) ^ 2 - sz[u]^2

发现只用知道x->root路径上的sz[u]的和，这个直接树剖维护即可

长链剖分：

长链剖分可以把维护子树中只与深度有关的信息优化到线性。
用来解决树上dp的维度里面有长度这个维度的优化
空间O(n), 时间O(n)!!!!!!!每个点在长链的顶端被合并一次
nlogn预处理， O(1)查询树上k级祖先:
维护贪心
数据结构维护长链

注意

f数组在dp以后就会被覆盖，也就是f[u][i]不一定表示u节点下面距离为i的了，可能已经变成1号节点为根的值了，所以如果有多组询问要把询问先存下来，用邻接表的存储关于u点的询问，在dfs的时候就直接更新
如果有g[son[u]] = g[u] - 1; 那么g的前后都需要h[v]的内存
nw += h[v]; g[v] = nw; nw += h[v]
合并上来的时候，f[v][j] 的j下标必须<h[v]
记得内部要dfs下
参考文献：
https://www.luogu.com.cn/blog/chen-zhe/zhang-lian-pou-fen-xiao-jie

例题:

P3565 [POI2014] HOT-Hotels

转化成一个点下面挂两个点，再再另一个子树找一个点。如果有g[son[u]] = g[u] - 1; 那么g的前后都需要h[v]的内存
nw += h[v]; g[v] = nw; nw += h[v]

k级祖先

跳2^{k以后的链一定>=2}k

所以维护从top,向上向下跳x步到达的位置(x <= 链长)

更为厉害

长剖+懒惰标记

这道题需要得到所有到u距离<=i 的点的权值和（每个点的权值是sz），由于长链是直接继承上来的，所以继承上来以后无法对于每一层都+=sz[u], 所以用tag的方式

继承的时候把下面的tag加上来，然后f[u][0] -= tag

代码里的细节见注释

注意：在tag更新的时候要更新f[u][0]

从根选择k条到叶子的路径，要求覆盖点权最大：按照路径长度剖分，选前k大

重建计划

这道题用数据结构维护长链，先分数规划，然后转化成L~R条边里面，路径最长的是谁

线段树的下标是id[u], id[u]+j表示距离u节点为j的所有点里面，路径最长为多少

然后合并，查询即可（同一个长链上，由于id连续，所以可以直接继承）

点分治

点分治基础

例题：

P4178 Tree

P3806 【模板】点分治 1

acwing 264. 权值

树上路径=k, <=k. 直接点分治统计

然后在calc里面：树状数组(map)/排序双指针

点分树

点分树基础

一共就两条性质：

第一种是：两个点在点分树上的lca, 一定在原树中两点的路径上。因为lca让两个点分开，所以一定在路径上。可以用这个来维护路径：

例如震波，开店

第二种就是: u点在点分树上的子树v，在原图中也是它的子树（或者祖先上的那个子树）

比如幻想乡，捉迷藏

震波

这道题把两点路径变成了枚举两个点的lca, 也就是不断往上跳

每一个节点u, ans += u节点处<=k-dis的个数

为了避免重复，还要 -= u的儿子v的子树中到u<=k-dis的个数

用树状数组和动态开点，都是nlogn的空间（后者*4）

动态开点，看似nlogn * logn 但是很多重复

这道题用树状数组，对于第一个树状数组，子树到自己的距离最多是sz[u]

对于第二个，虽然x和dfa[x]的距离在原树中不一定是1，但是由于dfa[x]的子树最多sz[u]个节点，所以开到sz[u]+1就可以了 (树状数组需要整体右平移)

如果是动态开点，开满了，也就多一个4*...（因为一个节点真正有效的只有1~sz[u]）

捉迷藏

这道题我们发现：

点分树上一个点u的不同儿子v, 一定在原图中u的不同子树里面（把u上方的那些点也当做一个子树）

所以我们每个子树传上来一个最大值即可

我们可以用一个堆维护： q[u]表示u子树的点到dfa[u]的距离集合
s[u]表示u的不同孩子送上来的最大值

ans表示答案序列

https://www.luogu.com.cn/problem/P3241

每个点维护一个年龄序列，按照年龄排序，维护一个距离前缀和

然后每一次二分，加上前缀和即可，因为lca(x,u)是dfa的时候，dfa集合内的点u到x的距离可以用u<->dfa + dfa<->x

注意：！！！getdis乘的数量，要排除掉当前子树

两个点在点分树上的lca, 一定在原树中，两点的路径上。因为lca让两个点分开，所以一定在路径上

https://www.luogu.com.cn/problem/P3345

一种从根节点向下走的思路，在原图上面：

如果从u->v 那么sum[v] * 2 > sum[u]

那么在点分树上面，对于u,假设原图中满足2sum>sum的点是x,点分树上的儿子是v,那么我们先走到v(因为x在v的子树), 此时得到的代价是

nsum[u] - fsum[u] + edge[i].w * (sum[u] - sum[v])

nsum/fsum 分别表示到u和dfa[u]， sigema si * di

同时我们还需要把x节点的d += sum[u] - sum[v]

因为之后从v移动的时候，如果走向点分树上的x,也一定在原图中靠近x,因为上面的sum[u]-sum[v]是直接链接x的，所以这样是对的

虚树

详细讲解

O(klogk)把树缩成只和关键点有关的大小

性质

虚树的点数<=2k-1, 分叉点的个数<=k-1, 无分叉链（所有点都没有分叉）的个数<=2k-1（考虑所有关键点及分叉点的父边）
所有dfs相邻两点的lca等于任意两点lca集合
虚树的链并，等于相邻两点距离和的1/2:(最后一个和开头也相邻)

虚树如果想要保留边权信息：如果是和：可以直接维护一个dis

如果是max, 可以用倍增或者树剖+st表

每一条边，暴力向上跳

注意

建树的时候是 while (id[lc] < id[stk[top-1]]) 是id[stk]!!!!!!!!!!
是lc != stk[top-1] 或者id[lc] != id[stk[top-1]]

Kingdom and its Cities

首先排除相邻的情况，然后用f[u]表示u子树满足两两不连通的答案

有时候dp的状态可以直接确定:比如这道题就可以直接确定子树内是否有通向子树外的关键点

g[u]表示上面的定义

如果u是关键点，那么g[u] = 1

如果u不是：假设u子树有两个g[u]=1的，那么这个时候一定要在u阻断，所以g[u] = 0，如果有0个，g[u]也等于0

否则，如果只有一个g[u] = 1的，那么之后在阻断一定不会更差，所以g[u] = 1,

假设子树的g的和为sum

如果是关键点: f[u] = sigema f[v] + sum g[u] = 1;

如果不是: f[u] = sigema f[v] + (sum >= 2) g[u] = sum == 1

消耗战
从1dfs到第一个im[u],这个点到1之间删除一条边即可

P4103 [HEOI2014] 大工程

任意两点距离和: 统计没一条边的工薪

最大/小距离: 类似dp求直径

寻宝游戏

动态插入,删除点，求最小包含生成树:

上面第3和结论，用set维护id排序的序列，然后维护距离和

七彩树

前置: https://www.luogu.com.cn/problem/CF893F

如果想要对S集合内的点到根（当做1）的路径上的所有点(相同算一次)，全部加上c

那么首先对于S集合的点+=c,然后对于S集合按照dfs序排序以后：

相邻的两个点的lca-=c。（头和尾不算）

然后每个点的权值就是子树和：

因为：对于一个点，假设内部有k个关键点，那么在内部的lca数是k-1（相邻的点求lca）,所以子树和正好+=c

如果想要把S集合的完整虚树上的点+=c,完整虚树的root = lca(a1, an)

那就相当于上面的去掉了root<->1的这些点

所以就在上面的基础上，对于fa[lca(a1, an)]-=c

回到这道题：

假设不考虑深度：一个颜色会被包含在它所有祖先节点的子树里，所以对于一种颜色集合S，我们需要把这些点到根的路径上的所有点(相同算一次)，全部加上1,代表有贡献。利用上面的差分，一个点子树的和，答案

因为有深度限制，那么就用前置里的可持久化线段树的思路，按照深度加点

然后每个颜色用一个set,按照id排序，维护lca即可

世界树

https://www.luogu.com.cn/blog/on-the-way/xu-shu-p3233-hnoi2014-shi-jie-shu

考虑异或k本质上是什么：首先对于n个数建立trie, 那么如果第k层是1, 就相当于把所有k层的左右孩子交换一下，对于一条从1~叶子链x, 原本的排名是a, 现在要求变成b, 那么需要+m(m = b - a)

x链的第i层如果是1, 那么交换以后会-=sz[i][0], 如果是0，交换以后会+=sz[i][1]

这个操作只会在有分叉点有用

那么这个就相当于一个可行性背包：用ai凑m

这个可以用bitset优化, bitset f[i]表示用前i个，能不能凑出来bitset对于的若干个m

转移f[i] = f[i-1], f[i] |= f[i-1] << ai; 或者 f[i] |= f[i-1] >> -ai(ai<0)

我们发现对于每一个n都求一遍好像比每一次询问都求要好，但是发现存不下

那么就离线下来，然后dfs这个trie

到达叶子就更新答案

这个图可以看成是n个叶子点和1为关键点的完整虚树,总点数依然是nlogn。但是有2个儿子的节点<=n-1个（因为每一个这样的节点合并两个关键点）。所以无分叉链的个数<=2n-1(叶子和分叉的节点)。所以只有2n-1个物品

总复杂度n^2/w 每一次转移O(m)

https://www.luogu.com.cn/problem/P4242

树剖维护颜色，虚树上dp, f[u]表示不考虑自己到自己，到子树内点的距离和

https://www.luogu.com.cn/problem/P6071

性质：一个点x加入虚树，他的父节点就是dfs序<id[x]的最大节点和它的lca, 以及dfs序>id[x]的最小节点和x的lca里面深度更大的那个

一个虚树的根，就是idmin和idmax的lca

https://www.luogu.com.cn/problem/P5439

我们发现直接计算每一个路径上的贡献不太好做，那么转换求和顺序，找每一对点被几个路径包含

那么就会产生两种思路：

点分治，或者分类讨论是否一个点是另一个点的祖先

方法1: 虚树
https://www.luogu.com.cn/blog/command-block/ds-ji-lu-p5439-xr-2-yong-heng

建立线性虚树：可以再点分治的时候把每个点属于的虚树编号都存下来，结束以后，从dfs序大的点到小的点遍历，加入到这个点所属的所有虚树里面，这样每个虚树的点都是从小往大排序的了（因为链式前向星是反着的）

方法2: 树剖
https://www.luogu.com.cn/blog/Owencodeisking/solution-p5439

对于lca(x,y) != x 且!=y, 这种情况就是sz[x] * sz[y] * dep(lca)

deplca这类的问题，可以转化成在T2上面x到根的路径上的点都+1，然后查询y到根的路径的和就行了

但是我们发现还有szx * szy 所以T2到根的路径都+szx, 然后最后的和再*szy就行了

对于第二种情况多算的，再去减掉就行

https://www.luogu.com.cn/problem/P5360

预处理前缀和后缀最小生成树

并且以左边一列和右边一列为关键点，建立虚树，每条边只保留最大的那条作为这条边的边权。然后存储一下如果把每一条边的最大边权都删掉，所得到的最小生成树的大小sum

以x列分裂的时候，就是1~x-1 和 x+1~m的生成树按照第1列和最后一列的最小生成树，中间的边的边权是最大的那条边，选择了就代表不删除，不选择就代表删除，不选择就代表不删除，不联通。

中间建立虚树的时候，可以用dfs的方式，只有son>=2或者是关键点再建立

https://www.luogu.com.cn/problem/CF526G

https://www.luogu.com.cn/blog/command-block/ds-ji-lu-cf526g-spiders-evil-plan

k条路径等价于叶子<=2k的树，所以就是一个x为root,选择<=2k个节点的最长路径（长链剖分）

如果多组询问，发现一定会有一个直径的端点被选择，所以以直径的端点作为根，然后调整覆盖x即可(注意，两个直径端点都可能),直径的端点一定是叶子，所以选择2y-1条

调整的时候，把x子树里面最深点t到根的路径加入。我们发现第2y-1条长链，要么出现在t的祖先中最深的地方(否则就不是最短的)，要么就不和t到祖先的路径重合

第一种情况找到后删掉后半部分，第二种，直接删掉2y-1这条

Boruvka

核心: 每个点选择一个最小的边，然后扩展

每一轮点数至少/2, 所以总共执行logn轮

应用范围：用于一类完全图，边数特别多的时候，转化成找到每个点的最小边
注意事项：

每一次的getto要提前，每一次要初始化g, 还有flag, bet函数在边权相同的时候不用按照第二关键字排序（一般写法需要）

例题：

https://www.luogu.com.cn/problem/CF888G

第一种是用boruvka, 然后每个集合开一个trie, 合并的时候启发式合并，每一次对于每个点在除去自己的trie里面找最小

第二种是发现一共有n-1个2个节点的点，这个节点的两侧各选择一个叶子，形成一条边，这个过程就是枚举左儿子的所有节点，然后在右儿子的子树找，找到最小的

https://www.luogu.com.cn/problem/AT_cf17_final_j

拆分成wx+disx+wy+disy-dislca, 对于每个x,求min wy+disy-dislca

为了防止同一个，就不同种类的最小值都记录一下，还要记录具体是哪个种类

void update(int u, ll x, int id) {
	if (x < f[u][0]) {
		if (id != g[u][0]) {
			f[u][1] = f[u][0]; g[u][1] = g[u][0];
		}
		f[u][0] = x; g[u][0] = id;
	} else if (x < f[u][1]) {
		if (id != g[u][0]) {
			f[u][1] = x; g[u][1] = id;
		}
	}
}

//!!!!!!!!!!如果边权有<0的，那么换根的时候有可能是错的，因为假设fa[v]=u
//f[u]的最小节点就在v里面，那么重复走一条负数可能会导致结果变小
//如果没有颜色的限制，我们同样可以利用0/1维护不同子树的min以及具体来自哪2个子树, 然后更新
//但是如果有，我们对于u，可以先正着枚举儿子然后反着枚举，维护一个前缀最小，然后更新子树dfs ,先进入儿子，再用儿子更新前缀最小。

https://www.luogu.com.cn/problem/P6199

两个dis不好计算，把其中一个树进行点分治，然后发现可以把dis转换成wi+wj

这个w是到当前分治中心的距离

然后建立虚树，像tree mst一样求一下就行了

这里建立虚树可以不用带log:
建立线性虚树：可以再点分治的时候把每个点属于的虚树编号都存下来，结束以后，从dfs序小的点到大的点遍历，加入到这个点所属的所有虚树里面，这样每个虚树的点都是从小往大排序的了（用vector存储）

最小斯坦纳树

基本思想：

fi, s表示以i为根，包含了s这些关键点的最小代价

转移：分类讨论i的度数, 如果不是1，那就考虑fi,sn + fi,s^sn。如果是1，那么就考虑是由j,s转移。

复杂度：第一个转移是n*3^n

第二个是mlogm*2^n

注意，先转移第一个，也就是同层的，然后转移不同层的

例题:

https://www.luogu.com.cn/problem/P4294

按照点权dp, 记录一下过来的方向

void dfs(int i, int s) {
	if (g[s][i] == -1) return;
	if (g[s][i] > 0) {
		dfs(i, g[s][i]); dfs(i, s ^ g[s][i]);
	}
	else {
		us[i] = 1; dfs(-g[s][i], s);
	}
}
for (int i = 1; i <= k; i++) us[key[i]] = 1;

us不一定把所有关键点都标记了，但是非关键点并且在树中的都标记了

圆方树

https://www.luogu.com.cn/blog/on-the-way/yuan-fang-shu

例题:

Prufer

https://www.luogu.com.cn/blog/on-the-way/prufer

支配树

https://www.luogu.com.cn/blog/on-the-way/zhi-pei-shu

最大团

https://www.luogu.com.cn/blog/on-the-way/bronkerbosch

环的计数

https://oiwiki.org/graph/rings-count/

例题1：如链接的t1

例题2：三元环计数

让度数小的指向度数大的(大链接小也行)，然后遍历出边，再遍历出边的出边是否能到达第一步的位置

注意：度数相同的时候要按照编号来比较大小

复杂度: msqrt(m) 证明: 相当于对于每一条边u->v, sigema out[v]

对于出度<sqrt(m)的点(一共m个边)，msqrtm

对于出度>sqrt(m)的点，它连出去的点的度数一定>sqrt(m), 所以最多sqrt(m)个，总共msqrt(m)

如果由重边，合到一起作为边的边权，然后每一个三元环提取出来三条边的权值的乘积用ed[i]表示来到i的那条边

例题3：四元环计数

具体思路：

每次找到最大点a, 然后找到由多少个c满足, (a,b) (b,c)有边（b,c都要小于a, 但是c不用小于b）

然后对于一个固定的c, ci有toti个，那么就是sigema C(toti,2)

然后清空tot数组

注意：一定是度数大的连接到度数小的

const int N = 1e5 + 10;
vector<int> e[N], g[N]; ll ans;
int n, m, deg[N]; int tot[N];
//!!!!!!!!!四元环必须是从大度数到小度数
//因为四元环： 先枚举有向边， 然后枚举的是原图的无向
//复杂度是: sigema in[u](对于每一个原图的无向)
//只有从大度数连到小度数， 才能保证in<=sqrt(n)   如果是从小->大， 那么是out<=sqrt(n)
//三元环计数， 按照in和out都可以算复杂度， 但是这个只能按照in算复杂度 
int main() {
	n = read(), m = read();
	for (int i = 1; i <= m; i++) {
		int u = read(), v = read();
		e[u].push_back(v); e[v].push_back(u);
		deg[u]++; deg[v]++;
	}
	for (int u = 1; u <= n; u++) {
		for (auto v : e[u]) {
			if (deg[v] < deg[u] || (deg[v] == deg[u] && v < u)) g[u].push_back(v);
			//因为一开始建立的就是双向的， 所以这样一定有一条是对的 
		}
	}
	for (int a = 1; a <= n; a++) { //a是最大点 
		for (auto b : g[a]) { //找到前面的b,然后找c。b,c都要<a
			for (auto c : e[b]) { //第二个是原图， 因为不要求c < b 只要求a是最大 
				if (deg[c] < deg[a] || (deg[c] == deg[a] && c < a)) { //!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!c不能大于a 
				//如果c = a也不能算 
				//因为a,b,c,d (a<b<c<d)和a,c,b,d都是合法的方案，所以第二次要用原图 
					ans += tot[c]; tot[c]++;
				}
			}
		}	
		for (auto b : g[a]) {
			for (auto c : e[b]) { //!!!!!!!!!!!!!!!!!!!!!!!!!!!记得清空 
				tot[c] = 0;
			}
		}	
	}
	cout << ans;
	return 0;
}

完美消除序列

https://www.cnblogs.com/onglublog/p/14507852.html

https://www.cnblogs.com/zhoushuyu/p/8716935.html

弦图判定：

先得到一个完美消除序列：lable的倒序(lable是当前节点和几个已经加入节点有边相连接）

然后判断每个a[i]和N(a[i])是否构成团， N(a[i])表示和a[i]有连边，在a[i]后面的点

复杂度O(n+m)


const int N = 1e3 + 10;
vector<int> e[N], to[N];//to表示所有lablei = x的有那些
int lab[N], rnk[N], a[N], n, m; //  num表示lablei 
void msc() {
	for (int i = 1; i <= n; i++) to[0].push_back(i); 
	int mx = 0;//表示当前最大的lable 
	for (int p = n; p >= 1; p--) {
		bool flag = 0; int x = 0;
		while (!flag) {
			for (int j = to[mx].size() - 1; j >= 0; j--) {
				int v = to[mx][j];
				if (!rnk[v]) {
					x = v; flag = 1; break;
				} else to[mx].pop_back();
			}
			if (!flag) mx--;
		} rnk[x] = p; a[p] = x;
		for (auto v : e[x]) {
			if (!rnk[v]) {
				to[++lab[v]].push_back(v); mx = max(mx, lab[v]);
			}
		}
	}
}
bool vis[N]; int tmp[N];
bool check() {
	//每一次找到有边的最近的那个 
	for (int i = 1; i <= n; i++) {
		int sz = 0; int u = a[i];
		for (auto v : e[u]) {
			if (rnk[v] > rnk[u]) {
				tmp[++sz] = v, vis[v] = 0; //所有有边的点 
				if (rnk[tmp[sz]] < rnk[tmp[1]]) swap(tmp[1], tmp[sz]);//tmp[1]是最靠前的 
			}
		}
		for (auto v : e[tmp[1]]) vis[v] = 1;
		for (int j = 2; j <= sz; j++) {
			if (!vis[tmp[j]]) return 0; //tmp[1]不能算 
		}
	}
	return 1;
}
void init() {
	for (int i = 1; i <= n; i++) {
		e[i].clear(); lab[i] = 0; rnk[i] = 0; to[i].clear();
	}
}

弦图的极大团

x + N(x)一定是一个合法的，我们预处理first[u], 表示第一个和u有连边的点

那么如果sz[u] >= sz[fst[u]] + 1, 说明fst被完全包含，就不要了，vis[fst[u]]=1. 那些vis[u]=0的点是合法的

最大团就是所有sz的max

弦图的色数

色数=最大团

//	for (int i = n; i >= 1; i--) { //方案 
//		int u = a[i];
//		for (auto v : e[u]) if (col[v]) vis[col[v]] = 1;
//		int c = 1; while (vis[c]) c++;//一定<=deg 
//		col[u] = c;
//		for (auto v : e[u]) if (col[v]) vis[col[v]] = 0;
//	} 
	int ans = 0;
	for (int i = 1; i <= n; i++) {
		int u = a[i]; int sz = 1;
		for (auto v : e[u]) {
			if (rnk[v] > rnk[u]) sz++;
		} ans = max(ans, sz); //等于最大团大小 
	}

弦图的最小团覆盖/独立集大小

显然一个团内只能取一个点，而独立集大小即为最小团覆盖。
对于序列中的每个点，把之后的点全部打上标记即可。

int ans = 0;
for(int q = 1; q <= n; q++) {
    int x = id[q];
    if(!vis[x]) {
        ans++;
        for(int i = head[x]; i; i = nxt[i])
            vis[ver[i]] = 1;
    }
}

全局最小割

https://www.luogu.com.cn/blog/on-the-way/stoer-wagner

图的绝对中心

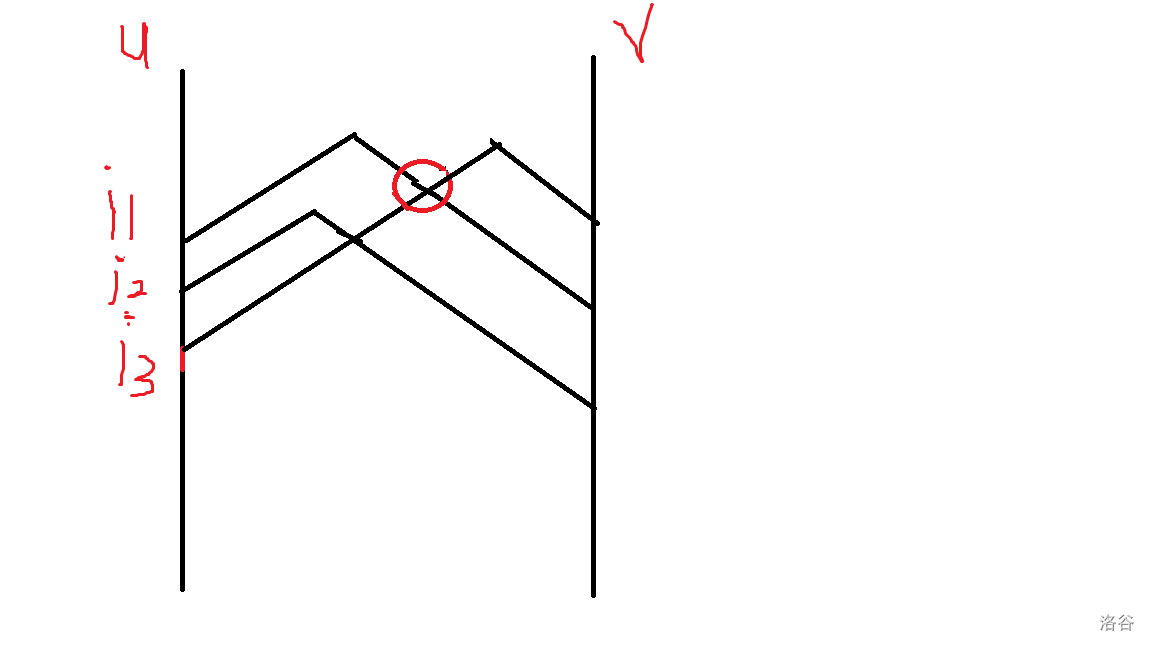
我们发现这些交点处是最优的地方（和u，v轴相交的就是中心在点上的情况）

交点的特征就是我们从距离u从大往小：i1->i2->i3

如果发现某一个点: dis[v][i3]>max(dis[v][i1,...i2])，那么就会出现交点

这个时候的长度就是dis[u][i3] + dis[v][maxindx:i1] + w, 因为红色交点表示的是i1更靠近v（下降阶段）, i3更靠近u(上升阶段）

最小直径生成树就是以绝对中心为根的最短路径树（记录一下每个点的最短路径是从哪里来的）

带花树

https://www.luogu.com.cn/blog/on-the-way/dai-hua-shu

Hall定理

https://www.cnblogs.com/came11ia/p/16676776.html

对于二分图中vl <= vr:存在vl的匹配当且仅当 vl中的任意一个集合S, 和S集合每个点出边构成的集合Q，S <= Q

拓展： vl<=vr的图里面最大匹配等于 vl - max(0,S-Q)

bzoj3693: 圆桌会议

这道题转换成左边人和右边的座位的完全匹配

!!!!!!!!!!!!!!!一定要判断vl<=vr, 如果vl>vr一定不成立

左边的人拆成ai个，就变成了，左边任意选择，右边必须大于左边

但是发现一组人一下子选完肯定限制更严格。

所以转化成若干个区间，每个区间有权值，看能不能选择若干个区间，ai的和>长度

把区间排序，假设选择了当前区间，线段树维护一下最左边区间是i的时候的值。找个最大值，比较一下是否大于0即可

这道题是环形的，所以还要2倍

上下界网络流

可行流，先把底线流满，算出每个点的in,out

如果in>out, 那么从s->i, 边权是in-out, sum += in-out

如果in<out 那么从i->t, 边权是out-in

判断最后dinic是否等于sum,等于就合法

每条边的流量是网络的流量+下界

上下界最大流

按照可行流建图，然后连ed->st inf

从s->t跑可行流，st->ed的反相边就是可行流，然后再从st->ed跑最大流（把ed->st的边删掉，edge[cnt].w = edge[cnt^1].w = 0）

结果相加是答案

最小流，按照最大流跑，只不过需要从ed->st跑最大流，结果是第一次-第二次

最小费用可行流（或者最大流也行？？？）：

按照可行流建边，然后跑费用流

线性规划转网络流

https://www.cnblogs.com/rainybunny/p/15700263.html

对于这个链接里面的套路适用于：

min: sigema buxi + sigema I * max(0, xu-xv-c)

如果bu>0 那么建立s->i的边，如果<0,那么建立i->t的

后面的链接v->u 上线为I, 费用为c的边

最后跑最小费用，相反数就是答案

对偶问题的转化：

大于小于号变，约束条件和结果边，变量变

比如：

min sigema xici

lim:

对于每个j,找到所有si<=j<=ti的xi求和: sigema xi >=aj

变成

max sigema yjaj

lim:

对于每个i, 找到所有si<=j<=ti的yj求和: sigema yj<=ci

ci和aj互换， <=和>=换， min和max换

xi和yj换（下标也换），枚举的范围也换(i->j)

平面图

点-边+面=2

https://www.luogu.com.cn/blog/on-the-way/ping-mian-tu

网格图最小割转最短路：

从左上角到右下角的最小割，从左到右和从上到下的边有用，所以所有边顺时针转90, 构造对偶图，从右上角到左下角的最短路

同余最短路

用来解决用若干个a,b,c,d,e....(假设a<=b<=c<=d...)

能不能凑出来某个数,或者能凑出来多少个<=k的

具体方法,任意一个数,我们把它放在最小模数a的剩余系里面

那么我们求一下用剩下的b,c,d...能凑出来%a=i的最小值是多少,记为h[i]

那么建图:

每个i到(i+b)%a 边权b, i到(i+c)%a 边权c

跑最短路,就是h[i]

判断能不能凑出n, 就是看一下h[n%a]是不是<=n

如果是,那么一定可以不断+a,凑到n

否则一定不行

判断能凑出来多少个<=的数

那么对于每一i, ans += (n-h[i])/a + 1

h[i]每当+a,就可以凑出来一个新的

对于2个的时候:

ax+by=n的解

相当于问by=n(mod a)

y = invb * n 对a取mod, 然后判断一下y*b是否>n,如果不大于,那么就合法

求=n的方案数，就是想跳楼机那样求一下前n-1的前缀和，然后求一下前n的前缀和。减一下就行了

例题:

https://blog.csdn.net/weixin_45750972/article/details/118581945

https://www.luogu.com.cn/problem/CF986F

标签：总结,sz,图论,cn,luogu,www,https,com
From： https://www.cnblogs.com/strywr/p/18283447

图论总结