[SHOI2012]随机树
题目背景
SHOI2012 D1T3
题目描述
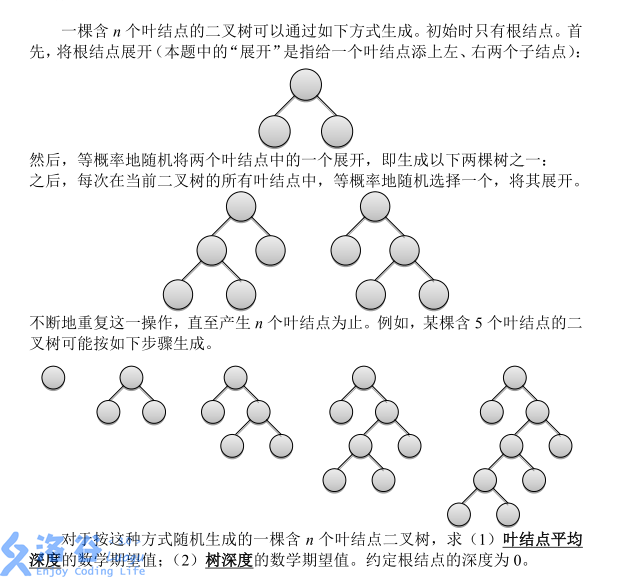
输入格式
输入仅有一行,包含两个正整数 q, n,分别表示问题编号以及叶结点的个数。
输出格式
输出仅有一行,包含一个实数 d,四舍五入精确到小数点后 6 位。如果 q = 1,则 d 表示叶结点平均深度的数学期望值;如果 q = 2,则 d 表示树深度的数学期望值。
样例 #1
样例输入 #1
1 4
样例输出 #1
2.166667
样例 #2
样例输入 #2
2 4
样例输出 #2
2.666667
样例 #3
样例输入 #3
1 12
样例输出 #3
4.206421
样例 #4
样例输入 #4
2 12
样例输出 #4
5.916614
提示

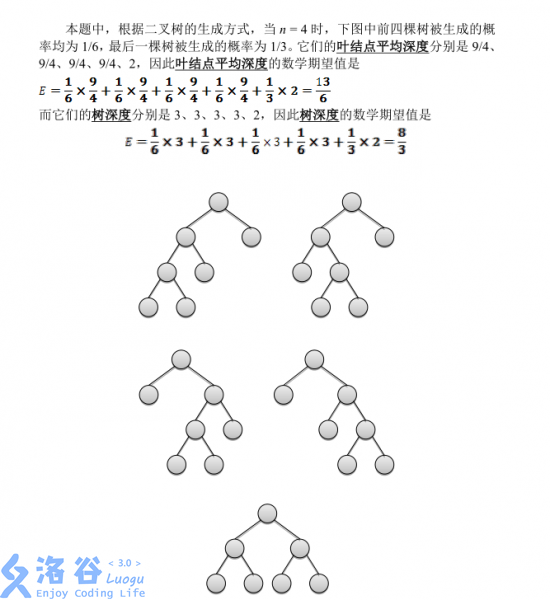
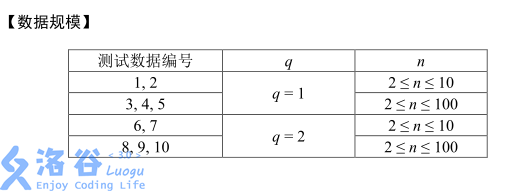
Solution
第一问其实不算难。设 \(f[x]\) 表示有 \(x\) 个叶子节点的树的叶子节点期望平均深度。会发现当我们随机选择一个节点进行扩展会对期望的深度的总和带来 \(f[x-1]+2\) 的贡献(两个节点的期望深度都是 \(f[x-1]+1\),因此新增加了 \(2\times (f[x-1] + 1)\) 的深度,原来被扩展的节点不再是叶子节点,因此深度和需要减去 \(f[x-1]\))。原来期望的深度总和为 \(f[x-1]\times (x-1)\),因此可以推出 \(f[x]\) 的转移方式:
\[\begin{matrix} f[x] & = &\displaystyle\frac {f[x-1] \times (x-1) + f[x-1] + 2} {x} \\ & = &\displaystyle \frac{f[x-1]\times x + 2}{x} \\ & = &\displaystyle f[x-1] + \frac 2 x \end{matrix} \]直接 \(\mathcal O (n)\) 转移即可。
难点在于第二问。
首先引入一个公式:整数期望公式
\(E(x) = \displaystyle\sum\limits_{i=1}^\infty P (i\le x)\)
其中 \(E(x)\) 表示随机正整数变量 \(x\) 的期望,\(P\) 表示概率。简单来说就是一个随机变量 \(x\) 的期望就是所有小于等于 \(x\) 的概率之和。有了这个式子,就可以通过概率来推导答案的期望了。
设 \(f[i][j]\) 表示 \(i\) 个叶子节点的时候,树的深度大于等于 \(j\) 的概率,根据上面那个公式可以得知答案是 \(\displaystyle \sum \limits_{i=1} ^ {n-1} f[n][i]\)。考虑怎么转移 \(f[i][j]\)。
考虑枚举生成的树的左右子树叶子节点的个数来转移,那么可以写出这样一个转移方程:
\[f[i][j] = \frac 1 {i-1} \sum \limits_{k = 1} ^ {i - 1} (f[k][j-1] + f[i-k][j-1] - f[k][j-1]\times f[i-k][j-1]) \]解释一下这个方程,其中 \(f[k][j-1]\) 表示左子树的叶子节点个数为 \(k\) 深度为 \(j-1\),此时可以从左子树扩展一个节点到深度 \(j\),同理,可以从右子树扩展一个节点到深度 \(j\)。但是会发现这样重复计算了左右子树同时拓展到深度 \(j\) 的情况,因此需要减去这部分重复的部分 \(f[k][j-1]\times f[i-k][j-1]\)。因为可选择的叶子节点的个数是 \(i-1\),而只有一个节点可以扩展到深度 \(j\),因此需要乘以 \(\displaystyle \frac 1 {i - 1}\)。
一切看起来都是那么的完美。真的就这样推出结论了吗?
并没有,因为我们并不知道是否选择其余的节点的概率是否是相等的(因为这些节点扩展出来的概率可能并不相等),因此需要证明的确是相等的。
这里的证明参考了这一篇题解的方法。
考虑构造一棵左子树包含 \(k\) 个叶节点,右子树包含 \(i-k\) 个叶节点的树,那么这棵树的深度大于等于 \(j\) 的概率 \(P_k\) 就是:
\[P_k = f[k][j-1] + f[i-k][j-1] - f[k][j-1] \times f[i-k][j-1] \]设构造出来这样的树的概率是 \(P_k'\),那么可以得知 \(i\) 个节点的随机构造出来的树的深度大于等于 \(j\) 的概率就是 \(\displaystyle \sum \limits _{k = 1} ^ {i-1} P_k \cdot P_k'\)。
因为我们要证明每个节点扩展出来的概率是相等的,因此只需要证明 \(\forall k_1, k_2 \in [1, i-1], P_{k_1}' = P_{k_2}'\) 即可。
考虑将生成这样的左子树有 \(k\) 个叶子节点,右子树有 \(i-k\) 个节点的树的序列写出来。设 \(\text{L}\) 表示在左子树扩展,\(\text{R}\) 表示在右子树扩展。那么整体的操作序列可以写作这样(总的操作次数是 \(i-1\) 次,并且第一次一定操作在根节点上,因此不讨论第一次操作):
\[\overbrace{\text{LRLLLRRRLR}\cdots} ^ {(k-1)\times \text L + (i-k-1)\times \text R} \]方案数就相当于是在 \(i-2\) 个位置中选择 \(k-1\) 个位置替换成为 \(\text{L}\),其它位置就表示为 \(\text R\),根据一点组合数学的知识就可以知道这样的方案数是 \(\displaystyle \begin{pmatrix}i - 2 \\ k - 1\end{pmatrix} = \frac{(i-2)!}{(k-1)!(i-k-1)!}\)。
接着考虑生成 \(k\) 个叶子节点的树的方案,显然第一次生成没得选择,只有一种方式,第二次因为有两个叶子节点,因此第二次生成的方案数为 \(2\),以此类推,第 \(k - 1\) 次操作的方案数就是 \(k-1\),综合起来就是生成 \(k\) 个叶子节点的树的方案数是 \((k-1)!\)。这就是左子树的所有可能的生成方案。
类似的,右子树因为有 \(i-k\) 个节点,需要 \(i-k-1\) 次操作,因此右子树的生成方案数是 \((i-k-1)!\)。将左右子树拼在一起,生成这样的一棵树的方案数是 \((k-1)!(i-k-1)!\),而 \(\text L,\text R\) 的先后顺序由操作序列控制,因此按照操作顺序生成这样的树的方案数是 \(\displaystyle(k-1)!(i-k-1)!\times \frac{(i-2)!}{(k-1)!(i-k-1)!} = (i-2)!\)。会发现这个方案数是与 \(k\) 无关的,也就是说不管左右子树的叶子节点数目是多少方案数都是相同的。举个例子说就是生成一棵左子树 \(1\) 个节点,右子树 \(114\) 个节点的方案数和生成一棵左子树 \(19\) 个节点,右子树 \(96\) 个节点的方案数是相同(尽管这相当反直觉)。
结合上述证明,可以得知随机构造出来的这样的树的各种概率是相等的,这样才能够直接对每个概率加和然后乘以 \(\displaystyle\frac 1 {i-1}\)。
对于边界的取值,很明显无论有多少个叶子节点,树的深度都是大于等于 \(0\) 的,也就是说 \(\forall i\in[1,n], f[i][0]=1\)。
推导过程非常复杂,但是与之对应的,代码难度非常的小。
Code
#include<bits/stdc++.h>
using namespace std;
int q, n;
double f[105][105];
void solve1() { // 问题 1,直接计算即可
double ans = 0;
for (int i = 2; i <= n; i++) ans += 2.0 / i;
cout << fixed << setprecision(6) << ans << '\n';
}
void solve2() {
for (int i = 1; i <= n; i++) f[i][0] = 1; // 边界值
for (int i = 2; i <= n; i++) {
for (int j = 1; j < i; j++) {
for (int k = 1; k < i; k++) // 不能从 0 开始,因为讨论一个没有节点的树的深度是无意义的
f[i][j] += f[k][j - 1] + f[i - k][j - 1] - f[k][j - 1] * f[i - k][j - 1];
f[i][j] /= i - 1;
}
}
double ans = 0;
for (int i = 1; i < n; i++) ans += f[n][i];
cout << fixed << setprecision(6) << ans << '\n';
}
signed main() {
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
cin >> q >> n;
if (q == 1) solve1();
else solve2();
return 0;
}
不得不说,写完这道题的代码和题解感觉对期望的理解增长了特别多。
标签:text,样例,times,displaystyle,P3830,深度,节点,SHOI2012,随机 From: https://www.cnblogs.com/hanx16msgr/p/16813878.html