说明:关于将象函数转为傅里叶变换,部分院校考研或期末考题会出现,但大部分辅导机构和网络资料枚举的例题对于这部分内容的阐述不全面,而杨晓非老师的《信号与系统(第二版》对这部分解析比较好,但有部分地方需要说明解释一下,故著以此章便于同学们理解。
1 傅里叶变换的存在性
首先需要考虑傅里叶的存在性,即收敛坐标的位置,若收敛边界在左半开面或虚轴上,则傅里叶变换存在,若在右半开面则不傅里叶变换不存在。
如下图所示:图(b),(c)的傅里叶变换存在

2 对于位于左半开面的象函数
1)若给出关于时间函数,将函数拉氏变换后,将即可
例2.1 指数衰减信号
,其收敛边界位于左半开平面,所以
3 对于位于虚轴上的象函数
总体公式是:
其中就是将
带入象函数中,而
需要分两种情况讨论
3.1 当 在
在 上有
上有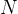 个单极点
个单极点
例3.1 求
的傅里叶变换
解:
由此可见,
存在两个单独的极点:
均位于虚轴上
其中
,
,
,
,带入公式为
3.2 当 在
在 上有重极点时
上有重极点时
例3.2 求
的傅里叶变换
解:由部分分式展开法
而
位于左半开面,所以直接带
,而
本身也需要
带入,所以相当于不用再带
部分的,而
带入公式即可,其中
(值得注意的是
时不需要管下面的阶乘)
4 举一反三
求 的傅里叶变换
本题答案后续公布
标签:函数,变换,傅里叶,带入,拉氏,虚轴,半开 From: https://blog.csdn.net/m0_67648017/article/details/140556047