神仙题目。
tips:后面把 \(4\) 个点说成一个组。
我们先考虑一个组怎么连才不是强联通的。
-
一个点 A 向另外三个点 BCD 连一条有向边。
-
在不满足第一种的情况下,BCD 向另一个点 A 连一条有向边。
-
AB 之间连有向边,CD 之间连无向边,然后 AC 和 AD 连一条有向边,BC 和 BD 也连一条有向边。
以上的三种情况没有重叠,可以覆盖所有非强连通组。
接下来我们只需要最小化这一些组数即可。
第一中:
假如第 \(i\) 个点的出度为 \(d_i\),那么这个点是第一个条件中的 A 的情况数为 \(C^3_{d_i}\)。
所以第一类总数为 \(\sum_{i = 1}^n C^3_{d_i}\)。并且 \(\sum_{i = 1}^n d_i = n \times \dfrac{n - 3}{2}\)。
又因为 \(C_x^3 = x(x - 1)(x - 2)\),所以在 \(x \ge 3\) 的情况下是个凸函数,那么:
\[\sum^n_{i = 1} C^3_{d_i} \ge n \times C^3_{\frac{n - 3}{2}} \]在 \(d_1 = d_2 = d_3 = \cdots \cdots = d_n\) 时,等号成立。所以最小值就是当 \(d_1 = d_2 = d_3 = \cdots \cdots = d_n = \dfrac{n - 3}{2}\) 时的答案。
所以第一组的总和为 \(n \times C^3_{\frac{n - 3}{2}} = \dfrac{n(n - 3)(n - 5)(n - 7)}{48} = \dfrac{n(n - 3)(n ^ 2 + 6 \times n - 31)}{48}\)。
第二和第三种:
这组通过构造可以是答案变为 \(0\)。构造方法如下:
首先我们需要满足第一组的条件,所以每一个点必须连 \(n - 1\) 条边,而其中有 \(\dfrac{n - 3}{2}\) 的边都是向外得边。
从这个点连出的的 \(1\) 到第 \(\dfrac{n - 3}{2}\) 条边都是从自己出发的有向边,第 \(\dfrac{n - 1}{2}\) 和第 \(\dfrac{n - 3}{2}\) 条边是无向边,其余的都是到自己的边。
当 \(n = 5\) 时,图长这样:
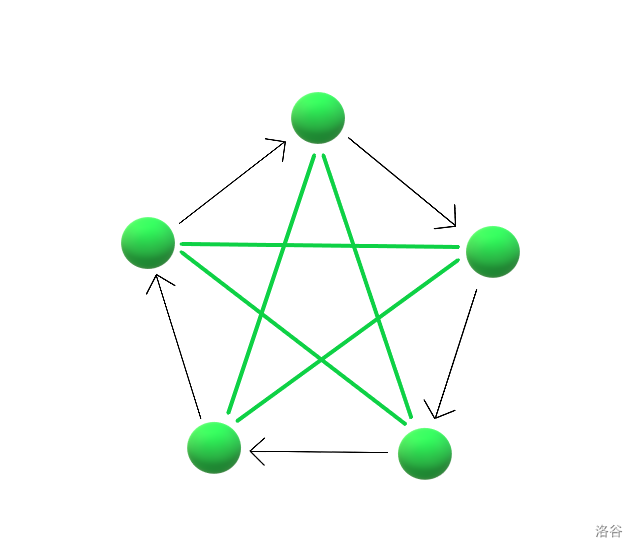
这样子就不能满足第二和第三种的条件了。所以这两种的答案为 \(0\)。
所以答案为 \(\dfrac{n(n - 3)(n ^ 2 + 6 \times n - 31)}{48}\)。
最后给出构造的代码:
for(int i = 1;i <= n;i++)
{
for(int j = i + 1;j <= i + (n + 1) / 2;j++)
{
a[i][(j - 1) % n + 1] = 1;
}
}