5 月 Div.2
场切:ABCDE
F 想出正解了,但是没写对拍 100->72,痛失 AK。
5 月 Div.1
场切:A(状压 DP)
B
TODO:
C
TODO:
D
简要题意:给定 \(n\)。你需要找一个数 \(w\),以 \(w\) 为参数画格子:在前 \(\lfloor \frac n w \rfloor\) 行每行画 \(w\) 个格子;紧接下来的一行画 \(n \bmod w\) 个格子紧贴左侧;以从上往下为第一关键字,从左往右为第二关键字,依次在格子中写上 \(1 \sim n\) 的数字。(下方有图解释)从 \(1\) 开始走,可以走到相邻(四连通)格子,不能走到质数格,目标为走到 \(n\)。找一个最小的 \(w\),使得目标被满足。保证 \(n\) 不为质数。可以证明答案必然存在。\(n \le 10^{24}\)。
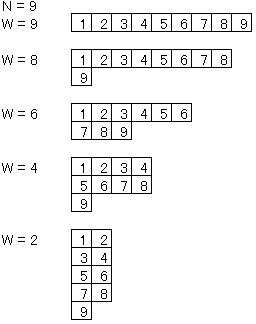
先写 BFS 暴力,观察可得,数据较小时无规律,数据较大时答案好像只有 \(8\) 和 \(14\)。
【赛时卡在此处】接下来不难了啊,我怎么就把这题给弃了呢!但凡仔细分析一下可知,\(n\) 足够大时,\(n \bmod 8 = 1\) 且 \(n-8\) 为质数时答案为 \(14\),否则答案为 \(8\)。
MR 判质数即可。(根据 OEIS A014233,\(10^{24}\) 范围内确定性判素可以用前 \(13\) 个质数)
6 月 Div.1
场切:A(环上 DP)
B
没想出正解,但是骗分骗到 48,非常好。
TODO:
C
想出正解了,但是 100->10。
简要题意:求 \(x\) 是数列 A010062(递推式:\(a_1 = 1, a_i = a_{i-1} + \text{popcount}(a_{i-1})\))的第几项(或报告 \(x\) 不在该数列中)。\(x \le 10^{12}\)。
TODO:
D
简要题意:已知 \(n,m,k\),求用 \(k\) 种不同颜色给 \(n \times m\) 的方格染色本质不同的方案数(\(\bmod 10^9 + 7\))。两种方案本质不同,当且仅当两种方案不能通过上下左右的循环移位得到。\(n,m,k \le 10^9\)。
前置知识:Burnside 引理。
令 \((a,b)\) 表示向右移 \(a\) 位,向下移 \(b\) 位的置换。
根据 Burnside 引理,可知答案为 \(\frac 1 {nm} \sum\limits_{(a,b)} \left( (a,b) \text{下的置换不变元个数} \right)\)。
\((a,b)\) 作用下的轨道长均相同,为 \(L = \text{lcm}(\frac n {\gcd(a,n)}, \frac m {\gcd(b,m)})\)。轨道个数为 \(\frac {nm} L\)。
对于置换不变元,同一根轨道上必须染同样颜色,每根轨道的染色方案互相独立,置换不变元个数为 \(k^{\frac {nm} L}\)。
指数太抽象,所以幂运算用 \(\text{pow}\) 代替。
\[\begin{aligned} & \frac 1 {nm} \sum\limits_{a=1}^n \sum\limits_{b=1}^m \text{pow}(k, \frac {nm} {\text{lcm}(\frac n {\gcd(a,n)}, \frac m {\gcd(b,m)})}) \\ =& \frac 1 {nm} \sum\limits_{d_1 | n} \sum\limits_{d_2 | m} \text{pow}(k, \frac {nm} {\text{lcm}(\frac n {d_1}, \frac m {d_2})}) \left( \sum\limits_{a=1}^n [d_1 | a] [\frac a {d_1} \perp \frac n {d_1}]\right) \left( \sum\limits_{b=1}^m [d_2 | b] [\frac b {d_2} \perp \frac m {d_2}]\right) \\ =& \frac 1 {nm} \sum\limits_{d_1 | n} \sum\limits_{d_2 | m} \text{pow}(k, \frac {nm} {\text{lcm}(\frac n {d_1}, \frac m {d_2})}) \varphi(\frac n {d_1}) \varphi(\frac m {d_2}) \\ =& \frac 1 {nm} \sum\limits_{D_1 | n} \sum\limits_{D_2 | m} \text{pow}(k, \frac {nm} {\text{lcm}(D_1, D_2)}) \varphi(D_1) \varphi(D_2) \\ \end{aligned}\]精细实现一点,分解质因数顺便把 \(\varphi\) 处理好,复杂度 \(O(d(n)d(m)(\log n + \log m))\)。
7 月 TG Day 1 图论
切 BCDEF。
A
XMOJ3353 是 BZOJ 原题。
简要题意:给定图,求 \(1 \to n\) 最短路。\(n \le 10^6, m \le 10^7\)。每个数据中有部分为随机生成。空间 256MB。
用 vector 存图会爆空间,需要用链式前向星。
直接二叉堆优化 Dijkstra 可过(\(O(m \log m)\) 为什么能过啊喂)。用 pbds 配对堆会 MLE。
卡常数:dis[n] 被求出之后直接退出 Dijkstra。
7 月 TG Day 2 膜你赛
A
是 NOIP 2006 原题,直接贴洛谷链接:P1066 [NOIP2006 提高组] 2^k进制数
场上懒得写高精度,用 int128 得 80pts。这样的策略事后证明是对的,我赛后高精度调了半天。
B
是 USACO 原题,直接贴洛谷链接:P3047 [USACO12FEB] Nearby Cows G
TODO:
C
TODO:
D
是 USACO 原题,直接贴洛谷链接:P1848 [USACO12OPEN] Bookshelf G
TODO:
7 月 TG Day 3 数据结构
切 ABCE。
TODO:
7 月 TG Day 4 膜你赛
个人评价:T1 黄 / 绿、T2 绿、T3 黄、T4 黄。
场切:A(种类并查集)
C 2log 被卡常 100->80,标答是基数排序,非常生气。
D(树状数组)场上写对忘交了 100->15,很傻逼。
B
TODO: