抽象代数的意义:\( \newcommand{\a}{\alpha} \newcommand{\b}{\beta} \newcommand{\D}{\Delta} \newcommand{\eps}{\varepsilon} \newcommand{\ph}{\varphi} \newcommand{\t}{\theta} \newcommand{\la}{\lambda} \newcommand{\si}{\sigma} \newcommand{\d}{\mathrm{d}} \newcommand{\e}{\mathrm{e}} \newcommand{\i}{\mathrm{i}} \newcommand{\N}{\mathbb{N}} \newcommand{\F}{\mathbb{F}} \newcommand{\Z}{\mathbb{Z}} \newcommand{\Q}{\mathbb{Q}} \newcommand{\R}{\mathbb{R}} \newcommand{\C}{\mathbb{C}} \newcommand{\fr}{\frac} \newcommand{\l}{\left} \newcommand{\r}{\right} \newcommand{\ov}{\overline} \newcommand{\ud}{\underline} \newcommand{\bs}{\backslash} \newcommand{\mps}{\mapsto} \newcommand{\op}{\operatorname} \newcommand{\Ker}{\operatorname{Ker}} \newcommand{\tr}{\operatorname{tr}} \newcommand{\abs}[1]{\left| #1 \right|} \newcommand{\infn}[1]{\| #1 \|_{\infty}} \newcommand{\an}[1]{\langle #1 \rangle} \newcommand{\scr}{\mathscr} \newcommand{\bf}{\mathbf} \newcommand{\rm}{\mathrm} \newcommand{\al}{\mathcal} \newcommand{\xeq}{\xlongequal} \newcommand{\bal}{\begin{aligned}} \newcommand{\eal}{\end{aligned}} \newcommand{\bc}{\begin{cases}} \newcommand{\ec}{\end{cases}} \newcommand{\bpm}{\begin{pmatrix}} \newcommand{\epm}{\end{pmatrix}} \newcommand{\bvm}{\begin{vmatrix}} \newcommand{\evm}{\end{vmatrix}} \)
- 对具有结合律的作用的抽象表示,相同的作用只要研究一遍。
- 研究不同作用所共有的性质,发展系统性的手段处理具有特定性质的作用。
- 最终发现特定性质的作用与研究它们的各种手段的广泛应用。
Chap.1 Introduction to Groups
群是具有结合律,存在单位元和逆元的抽象概念,只有作用在集合上才能体现出它的 “作用”。从群作用在集合上导出的对称性和其它性质是研究群的重要手段。事实上,很多群就是由此定义的。因此,很多人说群论是描述对称的理论。
A group is not really about symmetries of a particular object, it's an abstract way that things even can be symmetric. —— Grant Sanderson
*Sec.1.1 Basic Axioms and Examples
基本公理。非常基本,必须熟练掌握。
二元运算
集合 \(G\) 上的二元运算 \(\star\) 是 \(G\times G \to G\) 的函数 \(\star(a, b)\)。
- 若 \((a\star b)\star c = a\star (b\star c)\),则称 \(\star\) 具有 结合律。
- 若 \(a\star b = b\star a\),则称 \(\star\) 具有 交换律。
- 对 \(G\) 的子集 \(H\),若 \(H\) 的任意两个元素运算后仍属于 \(H\),则称 \(H\) 在 \(\star\) 下 封闭。
二元运算本身不要求结合律或交换律,自由度高。
群公理
集合 \(G\) 和其上的二元运算 \(\star\) 构成的有序组 \((G, \star)\) 称为 群(Group),若其满足以下三条公理:
(i) \(\star\) 有结合律。
(ii) 存在单位元 \(e\),满足 \(a\star e = e\star a = a,\ \forall a\in G\)。
(iii) 每个元素存在逆元 \(a ^ {-1}\),满足 \(a \star a ^ {-1} = a ^ {-1} \star a = e,\ \forall a\in G\)。
\(G\) 的大小称为 阶(Order),记作 \(|G|\)。\(G\) 不一定有限,但公理 (ii) 保证 \(G\) 非空。由有限集定义的群称为 有限群。
群公理暗含了 \(G\) 对 \(\star\) 运算的封闭性。
结合律是几乎所有作用的内在性质:函数复合具有结合律。
单位元说明 “什么也不做” 是一种对称。
逆元说明对称作用的逆作用(反悔)也是一种对称(这也是一种对称)。
阿贝尔群
运算具有交换律的群称为 阿贝尔群(Abelian Group)。
简要记号
一般视 \(\star\) 为元素的乘法运算(记号,不是数学乘法),\(a\star b\) 记为 \(ab\),单位元 \(e\) 记为 \(1\)。
对 \(n\in \Z ^ +\),记 \(x ^ n = xx\cdots x\),共 \(n\) 项;记 \(x ^ {-n} = x ^ {-1}x ^ {-1}\cdots x ^ {-1}\),共 \(n\) 项;令 \(x ^ 0 = 1\)。定义的合理性由性质 1.1 第五条保证。
特殊情况视 \(\star\) 为元素的加法运算(记号,不是数学加法),\(a\star b\) 记为 \(a + b\),单位元 \(e\) 记为 \(0\),逆元记为 \(-a\)。例如环要求 \(G\) 上定义加法和乘法,且 \((G, +)\) 构成阿贝尔群。类似有 \(nx, -nx\) 和 \(0x\)。
性质 1.1(基本性质)
(1) 单位元唯一。
(2) 每个元素的逆元唯一。
(3) \((a ^ {-1}) ^ {-1} = a\)。
(4) \((ab) ^ {-1} = b ^ {-1} a ^ {-1}\)。
(5) 广义结合律:\(a_1a_2\cdots a_n\) 的结果与括号位置无关。
以 (2) 为例:假设 \(b, c\) 都是 \(a\) 的逆元,则 \(ab = 1\) 且 \(ca = 1\),于是 \(c = c1 = cab = 1b = b\)。
性质 1.2(消去律)
(1) \(au = av \implies u = v\)。
(2) \(ub = vb\implies u = v\)。
以 (1) 为例:\(au = av\implies a ^ {-1}au = a ^ {-1}av \implies 1u = 1v \implies u = v\)。
像解方程一样将元素在等式左右移动。
注意:必须同时左乘或同时右乘。\(a = a\),但 \(xa\) 不一定等于 \(ax\)。
阶
最小的正整数 \(n\) 满足 \(x ^ n = 1\) 称为 \(x\) 的阶,记作 \(|x|\)。当 \(G\) 为无限群时,\(n\) 可能不存在,此时认为 \(|x|\) 无穷大。
有没有很熟悉?和数论的阶是同一个概念。模 \(n\) 下的简化剩余系就是群 \((\Z / n\Z) ^ \times\)。
*Sec.1.2 Dihedral Groups
基本群之一。
二面体群
考虑所有使正 \(n\) 边形保持原状的作用(刚体运动,必须恰好落在原来的位置):绕中心旋转 \(\fr {2k\pi} {n}\) 弧度,其中 \(0\leq k < n\)。
如果将正 \(n\) 边形视为三维空间中的二面体,则翻转导出了更多的作用。所有这些作用构成的群称为 \(2n\) 阶 二面体群(Dihedral Groups) \(D_{2n}\),因为 \(|D_{2n}| = 2n\)。\(1\) 有 \(n\) 种方案,\(2\) 有两种方案,剩下的点由 \(1, 2\) 的位置确定。
注意:对于 \(D_4\),将二面体旋转 \(\pi\) 弧度和沿线段的垂直平分线翻转是两种不同的对称作用。后者改变了二面体的正反。
注意:\(D_{2n}\) 是 \(n\) 边形对应的二面体群,不是 \(2n\) 边形。
为什么能构成群?
- 对二面体的作用满足结合律。
- 不进行任何操作也是一种保持形状的作用,它是群的单位元。
- 刚体运动可逆,且保持形状的作用的逆作用保持形状,所以逆元存在。
记 \(r\) 表示绕中心顺时针旋转 \(\fr {2 \pi} n\) 弧度,\(s\) 表示以 \(1\) 和中心的连线为轴翻转,则
(1) \(1, r, \cdots, r ^ {n - 1}\) 互不相同,所以 \(|r| = n\)。
(2) \(|s| = 2\)。
(3) 对任意 \(i\),\(s\neq r ^ i\)。
(4) 对任意 \(0\leq i, j < n\) 且 \(i\neq j\),\(sr ^ i\neq sr ^ j\)。
(5) \(rs = sr ^ {-1}\)。
(6) \(r ^ is = sr ^ {-i}\)。
注意:作用的复合从右向左,\(rs\) 表示先执行 \(s\),再执行 \(r\),与函数复合的顺序一致。这一点很重要。
容易根据实际意义证明这些性质。
(5) 是二面体群最核心的性质,(6) 是 (5) 的直接推论:它揭示了 \(s\) 如何与 \(r\) 的幂次交换,于是 \(D_{2n}\) 的所有元素可以写成 \(s ^ ir ^ j\) 的形式,其中 \(0\leq i < 2\),\(0\leq j < n\),因为总可以将 \(r\) 右侧的 \(s\) 挪到它左侧。类似地,总可以将 \(r\) 左侧的 \(s\) 挪到它右侧,用 \(r ^ is ^ j\) 表示所有元素。
生成元和关系
二面体群由 \(r, s\) 和一些关系生成。推广这个思想,称 \(G\) 被集合 \(S\) 生成,若 \(G\) 的每个元素由 \(S\) 的元素和它们的逆元有限相乘得到,记作 \(G = \an {S}\)。\(S\) 称为 \(G\) 的 生成元(Generator)。
为什么要有逆元?阶不一定存在,考虑 \(\Z = \an{1}\)。对于有限群则不需要逆元。
由群的封闭性可知 \(S\) 中元素的乘积集合等于 \(G\),而不只是包含 \(G\)。
\(S\cup \{1\}\) 的元素之间的等式 \(R_1, R_2, \cdots, R_m\) 称为 关系(Relation),如 \(D_{2n}\) 有关系 \(r ^ n = s ^ 2 = 1\) 和 \(rs = sr ^ {-1}\)。
\[G = \an {S \mid R_1, R_2, \cdots, R_m} \]称为 \(G\) 的 表示(Representation)。于是
\[D_{2n} = \an {r, s \mid r ^ n = s ^ 2 = 1,\ rs = sr ^ {-1}} \]这些关系唯一确定了 \(D_{2n}\)。任何其它满足这些关系的群一定满足某些无法由这些关系推出的其它关系。
寻找一个群的表示是困难的(况且表示不一定唯一),涉及高深的表示论内容。
Sec.1.3 Symmetric Group
基本群之二。
对称群
所有 \(n\) 阶排列构成 \(n\) 阶 对称群(Symmetric Group)。\(S_{\Omega}\) 表示所有双射 \(\sigma : \Omega \to \Omega\) 构成的集合,\(S_n\) 表示 \(\Omega = \{1, 2, \cdots, n\}\),\(|S_n| = n!\)。
排列就是把集合双射到自身。
对 \(n\geq 3\),\(S_n\) 不是阿贝尔群。
环表示
环
\[(a_1\; a_2\; \cdots\; a_n) \]表示 \(a_i\mps a_{i + 1}\),\(a_n\mps a_1\),其它位置不变。不要把顺序搞反了。
不交的环是可交换的。
环分解算法
从每个点开始跳出边。OI 基本算法。
一个排列的阶是它的环分解中所有环的环长的最小公倍数。
Sec.1.5 The Quaternion Group
四元数群
\[Q_8 = \{\pm 1, \pm i, \pm j, \pm k\} \]满足 \(1\) 为单位元,\(-1\) 的作用是改变符号。
乘法的顺序是 \(i, j, k\),即 \(ij = k\),\(jk = i\),\(ki = j\),交换顺序反号。特别地,\(i ^ 2 = j ^ 2 = k ^ 2 = -1\)。
\[Q_8 = \an {i, j} \]*Sec.1.6 Homomorphisms and Isomorphisms
同态
同态是一个群到另一个群的保持结构的映射。对 \((G, \star)\) 和 \((H, \diamond)\),映射 \(\ph : G\to H\) 称为 同态(Homomorphism),若
\[\ph(x\star y) = \ph(x) \diamond \ph(y),\ \forall x, y\in G \]或简写为
\[\ph(xy) = \ph(x)\ph(y) \]同构
同构是两个群之间保持结构的映射。映射 \(\ph\) 称为 同构(Isomorphism),若它既是同态,也是双射。如果两个群同构,则它们拥有完全相同的结构性质,除了元素表示不同,它们在其它所有方面都是相同的。
表示同构的二元关系符为 \(\cong\)(\cong)。\(G\cong G\),\((\R, +) \cong (\R ^ + , \times)\)(指数和对数),\(S_{\Delta} = S_{\Omega} \iff |\Delta| = |\Omega|\)。
同构的意义:
- 同构的群只需要研究其中一个。
- 具有相同性质的群同构。
同态的意义:设 \(G\) 的像集为 \(K\)。
- 若 \(\ph\) 是单射,则 \(H\) 存在子结构(子群)\(K\) 和 \(G\) 同构。
- 若 \(\ph\) 不是单射,则同态相当于将 \(G\) “折叠” 成若干几乎和 \(K\) 同构的部分(陪集),每一份在映射后均得到 \(K\)。引出商群的概念:映射到相同元素的元素坍缩成一个元素,那么 \(G\) 坍缩成和 \(K\) 同构的商群,自然地有第一同态定理 \(G / \ker \ph \cong K\)。
同态与表示
对 \(G = \an {s_1, \cdots, s_m}\),\(H = \{r_1, \cdots, r_m\}\),若 \(G\) 的关系将 \(s_i\) 替换为 \(r_i\) 后仍成立,则存在唯一同态 \(\ph : G\to H\) 将 \(s_i\) 映到 \(r_i\)。
若 \(H = \an {r_1, \cdots, r_m}\),则 \(\ph\) 是满射,因为将乘积中的 \(r_i\) 替换为 \(s_i\) 即得一个原像。但 \(\ph\) 不一定是单射,因为 \(H\) 的关系可能更强。此时若 \(|G| = |H|\),则 \(\ph\) 是单射,推出 \(\ph\) 是双射,\(G\cong H\)。
Sec.1.7 Group Actions
群作用在集合上导出的性质一定程度上反映了群本身的结构性质。
群作用
映射 \(G\times A\to A\)(写作 \(g\cdot a\))是群 \(G\) 在集合 \(A\) 上的 群作用(Group Action),若
(1) \(\forall g_1, g_2\in G,\ a\in A : g_1\cdot( g_2 \cdot a) = (g_1g_2) \cdot a\)。
(2) \(\forall a\in A : 1\cdot a = a\)。
即单位元保持元素不动且满足结合律。\(\cdot\) 通常省略不写,注意它不是二元运算。
作用的排列表示
对每个 \(g\in G\) 定义映射 \(\si_g : A \to A\),其中 \(\si_g(a) = g\cdot a\)。
(1) \(\si_g\) 是 \(A\) 的排列,因为 \(\si_g \circ \si_{g ^ {-1}}\) 是单位排列,即 \(\si_g\) 有逆映射。
(2) 定义映射 \(\ph : G\to S_A\),其中 \(\ph(g) = \si_g\),则 \(\ph\) 是同态。\(\ph\) 称为对应作用的 排列表示(Permutation Representation)。
因为 \(g\) 作用在 \(A\) 上得到 \(A\) 的排列,所以 \(g\) 构成的群就是 \(A\) 的若干排列构成的群。不同的 \(g\) 的作用可以相同,所以 \(\ph\) 不是单射。
反之,给定 \(G\to S_A\) 的同态,由该同态唯一确定了 \(g\) 在 \(A\) 上的一个作用。
Chap.2 Subgroups
揭示某种数学对象的结构的基本手段是研究其满足相同公理的子集。
Sec.2.1 Definition and Examples
子群
称 \(G\) 的子集 \(H\) 是 \(G\) 的 子群(Subgroup),若 \(H\) 非空且在乘积和逆元下封闭,即 \(\forall x, y\in H : x ^ {-1}, xy\in H\)。记作 \(H\leq G\)。\(H < G\) 强调了 \(H\neq G\)。
对任意 \(x\in H\),\(x ^ {-1}\) 在 \(H\) 和 \(G\) 中相等,所以该符号是良定义的。
群判定是一项繁琐的工作,因为需要检查群公理,尤其是结合律。但子群判定只需要检查乘积和逆的封闭性。
子群具有 传递性:若 \(K\leq H\) 且 \(H\leq G\),则 \(K\leq G\)。特别地,若 \(K, H\leq G\) 且 \(K\subseteq H\),则 \(K\leq H\)。
性质 2.1(子群判别法)
\(G\) 的子集 \(H\) 是 \(G\) 的子群当且仅当
(1) \(H\neq \varnothing\),且
(2) \(\forall x, y \in H : xy ^ {-1}\in H\)。
证明:\(\forall x, y\in H : xx ^ {-1} = 1,\ 1y ^ {-1} = y ^ {-1},\ x(y ^ {-1}) ^ {-1} = xy\)。
(2) 将乘积和求逆结合为一条限制。特别地,若 \(H\) 有限,则可只检查 \(H\) 非空且乘积封闭,因为 \(x ^ {|x| - 1} = x ^ {-1}\)。
*Sec.2.2 Centralizers and Normalizers, Stabilizers and Kernels
一些重要的基本概念的定义。设 \(A\) 是 \(G\) 的任意非空子集。
中心化子
定义
\[C_G(A) = \{g\in G \mid gag ^ {-1} = a,\forall a\in A\} \]为 \(A\) 在 \(G\) 中的 中心化子(Centralizer)。
\(gag ^ {-1} = a\) 即 \(ga = ag\)。\(C_G(A)\) 是 \(G\) 中和 \(A\) 的所有元素交换的元素集合。
因为 \(xyay ^ {-1} x ^ {-1} = xax ^ {-1} = a\) 且 \(gag ^ {-1} =a\implies a = g ^ {-1}ag\),所以 \(C_G(A)\leq G\)。
中心
定义
\[Z(G) = \{g\in G\mid gx = xg, \forall x\in G\} \]为 \(G\) 的 中心(Center)。
\(Z(G)\) 是 \(G\) 中和 \(G\) 的所有元素交换的元素集合。
因为 \(Z(G) = C_G(G)\),所以 \(Z(G)\leq G\)。
正规化子
定义 \(gAg ^ {-1} = \{gag ^ {-1} \mid a\in A\}\)。由消去律可知 \(|A| = |gAg ^ {-1}|\)。定义
\[N_G(A) = \{g\in G\mid gAg ^ {-1} = A\} \]为 \(A\) 在 \(G\) 中的 正规化子(Normalizer)。
\(gAg ^ {-1} = A\) 即存在 \(a'\in A\) 使得 \(ga = a'g\)。\(N_G(A)\) 是 \(G\) 中和 \(A\) 可交换的元素集合。因为和 \(A\) 的所有元素交换则和 \(A\) 交换,所以 \(C_G(A)\subseteq N_G(A)\)。中心化子的条件强于正规化子。
因为 \(xyay ^ {-1}x ^ {-1} = xa'x ^ {-1} = a''\in A\) 且 \(gAg ^ {-1} = A \implies A = g ^ {-1}Ag\)(\(gAg ^ {-1}\to A\) 是双射),所以 \(N_G(A)\leq G\)。可知 \(C_G(A)\leq N_G(A)\)。
\(G\) 的每个元素和 \(A\) 可交换是 \(G\) 可将 \(A\) 坍缩为 \(1\) 的充要条件,否则存在元素无法和单位元交换。\(A\) 可以作为商群的陪集当且仅当 \(N_G(A) = G\),即 \(A\unlhd G\)。
群作用的稳定子与核
令 \(G\) 作用在集合 \(S\) 上,定义
\[G_s = \{g\in G\mid g\cdot s = s\} \]为 \(s\in S\) 的 稳定子(Stabilizer)。
定义
\[\{g\in G\mid g\cdot s = s,\forall s\in S\} \]为群作用的 核(Kernel),它是所有 \(G_s\) 的交。
显然 \(G_s\leq G\),核也是 \(G\) 的子群。
稳定化子,正规化子和中心是子群是稳定子与核是子群的特例。
设 \(S = \mathcal{P}(G)\) 表示 \(G\) 的所有子集构成的集合。定义 \(G\) 在 \(S\) 上的 共轭(Conjugation)作用 为 \(\forall B\subseteq G : B\mps gBg ^ {-1}\)。\(N_G(A)\) 是 \(A\) 的稳定子,所以 \(N_G(A)\leq G\)。
设 \(S = A\),考虑 \(N_G(A)\) 在 \(A\) 上的共轭作用,即 \(\forall a\in A : a\mps gag ^ {-1}\)(由 \(N_G(A)\) 的定义,这确实是一个群作用)。\(C_G(A)\) 是作用的核,所以 \(C_G(A)\leq N_G(A)\)。
考虑 \(G\) 在自身上的共轭作用。\(Z(G)\) 是作用的核,所以 \(Z(G)\leq G\)。
*Sec.2.3 Cyclic Groups and Cyclic Subgroups
OIer 最熟悉的一集。
循环群
\(H\) 称为 循环群(Cyclic Group),若 \(H\) 仅由一个元素生成。即
\[H = \{x ^ n \mid n\in \Z\} = \an {x} \]其中 \(|x|\) 决定了 \(H\) 的大小。
OI 最常涉及到的循环群是模 \(p\) 意义下的加法群 \(\Z / n\Z\),它可以看成加性群 \(\an {1 \mid p1 = 0}\)。
性质 2.2
若 \(H = \an {x}\),则 \(|H| = |x|\)。具体地:
(1) 若 \(|H| = n < \infty\),则 \(x ^ n = 1\) 且 \(1 = x ^ 0, x ^ 1, x ^ 2, \cdots, x ^ {n - 1}\in H\) 互不相同。
(2) 若 \(|H| = \infty\),则不存在 \(n\in \Z\backslash \{0\}\) 使得 \(x ^ n = 1\),且 \(\forall a\neq b\in \Z : x ^ a \neq x ^ b\)。
性质 2.3
对群 \(G\) 的任意元素 \(x\),若 \(x ^ m = x ^ n = 1\),则 \(x ^ {\gcd(n, m)} = 1\)。特别地,若 \(x ^ m = 1\),则 \(|x| \mid m\)。其中 \(n, m\in \Z\)。
注意 \(G\) 不需要是循环群。
定理 2.4
阶相同的循环群同构。
记 \(Z_n\) 表示 \(n\) 阶循环群。\(Z_n\) 强调乘法,\(\Z / n\Z\) 强调加法。
接下来刻画每个元素的阶。
性质 2.5
令 \(x\in G\),\(a \in \Z - \{0\}\)。
(1) 若 \(|x| = \infty\),则 \(|x ^ a| = \infty\)。
(2) 若 \(|x| = n < \infty\),则 \(|x ^ a| = \fr {n} {\gcd(n, a)}\)。
(3) 特别地,若 \(|x| = n < \infty\) 且 \(a\mid n\),则 \(|x ^ a| = \fr n a\)。
证明 (2):设 \(d = \gcd(n, a)\),\(n = db\),\(a = dc\),\(y = x ^ a\),则 \(b\perp c\),需要证明 \(|y| = b\)。一方面
\[y ^ b = x ^ {ab} = x ^ {dcb} = (x ^ n) ^ c = 1 \implies |y| \mid b \]另一方面
\[y ^ {|y|} = 1 \implies x ^ {dc|y|} = 1 \implies n\mid dc|y| \implies b\mid c|y| \stackrel {b\perp c}{\implies} b\mid |y| \]所以 \(|y| = b\)。
相当于求最小的 \(k\) 使得 \(n\mid ka\),即 \(k = \fr {n} {\gcd(n, a)}\)。
和 OI 数论中的阶一模一样!它们完全是同一个概念。
性质 2.6
令 \(H = \an {x}\)。
(1) 若 \(|x| = \infty\),则 \(H = \an {x ^ a}\) 当且仅当 \(a = \pm 1\)。
(2) 若 \(|x| = n < \infty\),则 \(H = \an {x ^ a}\) 当且仅当 \(a\perp n\)。这样的 \(a\) 的数量为 \(\ph(n)\)。
定理 2.7
令 \(H = \an {x}\)。
(1) \(H\) 的所有子群都是循环群。若 \(K\leq H\),则 \(K = 1\) 或 \(\an {x ^ d}\),其中 \(d\) 是最小的正整数使得 \(x ^ d\in K\)。
(2) 若 \(|H| = \infty\),则对任意两个不同的非负整数 \(a, b\),\(\an {x ^ a}\neq \an {x ^ b}\)。\(\an {x ^ m} = \an {x ^ {|m|}}\)。
(3) 若 \(|H| = n < \infty\),则对 \(n\) 的每个正因数 \(a\),都存在 \(a\) 阶循环子群 \(\an {x ^ d}\),其中 \(d = \fr n a\)。对所有整数 \(m\),\(\an {x ^ m} = \an {x ^ {\gcd (n, m)}}\),所以 \(H\) 的子群和 \(n\) 的正因数一一对应。
一些情况下有限群和无限群需要分开考虑。
对于 OI 水平较高的读者,Section 2.3 的所有内容应当是非常显然的。
Sec.2.4 Subgroups Generated by Subsets of a Group
给定集合 \(A \subseteq G\),包含 \(A\) 的最小子群是什么样的?
性质 2.8
如果 \(\mathcal A\) 是 \(G\) 的子群集合,那么 \(\mathcal A\) 的所有元素的交也是子群。
集合的生成子群
令 \(A\) 是 \(G\) 的任意子集,定义 \(\an {A}\) 为 \(G\) 的所有包含 \(A\) 的子群的交,即
\[\an {A} = \bigcap_{A\subseteq H\leq G} H \]称为 由 \(A\) 生成的 \(G\) 的子群。
当 \(A\) 是有限集 $ {a_1, a_2, \cdots, a_k}$ 时,也写作
\[\an {a_1, a_2, \cdots, a_k} \]以及记
\[\an {A, B} := \an {A\cup B} \]定义
\[\ov A = \{a_1 ^ {\epsilon_1} a_2 ^ {\epsilon_2} \cdots a_n ^ {\epsilon_n} \mid n \in \Z, \ n\geq 0,\ \forall i : a_i\in A,\ \epsilon_i = \pm 1\} \]即 \(A\) 及其逆元的有限乘积集合。
实际上 \(\ov A\) 更符合 “生成” 的观念,前一种定义保证了 \(A\) 的生成子群的存在和唯一性。
性质 2.9
\[\ov A = \an {A} \]首先有 \(\ov A\leq G\)。
由 \(A\subseteq \ov A\) 知 \(\ov A \in \mathcal {A}\)(\(\mathcal {A}\) 的定义见性质 2.8),再由 \(\an {A}\) 的定义知 \(\an {A}\subseteq \ov A\)。
又因为 \(A\subseteq \an {A}\) 且 \(\an {A}\) 是群,所以 \(\ov A\) 的任何元素属于 \(\an {A}\),即 \(\ov A \subseteq \an{A}\)。
生成子群的阶
合并相邻相同的元素,得
\[\an {A} = \{a_1 ^ {\a_1} a_2 ^ {\a_2}\cdots a_n ^ {\a_n} \mid n\in \Z,\ \forall i : a_i\in A,\ \a_i \in \Z,\ a_i \neq a_{i + 1}\} \]对阿贝尔群 \(G\),因为相邻元素可交换,所以当 \(A\) 是有限集 \(\{a_1, a_2, \cdots, a_k\}\) 时,有
\[\an {A} = \{a_1 ^ {\a_1} a_2 ^ {\a_2}\cdots a_k ^ {\a_k} \mid \forall i : \a_i \in \Z\} \]进一步地,当 \(|a_i| = d_i < \infty\) 时,\(|\an {A}| \leq d_1 d_2 \cdots d_k\)。
若 \(G\) 不是阿贝尔群,情况复杂得多。对于 \(G = GL_2(\R)\),\(a = \bpm 0 & 1 \\ 1 & 0 \epm\),\(b = \bpm 0 & 2 \\ \fr 1 2 & 0 \epm\),有 \(a ^ 2 = b ^ 2 = 1\) 但 \(ab = \bpm \fr 1 2 & 0 \\ 0 & 2 \epm\),\(|ab| = \infty\),所以 \(\an {a, b}\) 是由两个阶为 \(2\) 的群生成的无限群。
Sec.2.5 The Lattice of Subgroups of a Group
一种可视化有限群子群关系的结构。
格
用以下方法构建有限群 \(G\) 的子群的 格(Lattice)。
(1) 写下所有子群,\(1\) 在底部,\(G\) 在顶部。大致地,阶更大的子群位置更高。
(2) 若 \(A < B\) 且 \(A, B\) 之间没有其它子群 \(A < C < B\),则从 \(A\) 向上到 \(B\) 连线。
最终形成入度和出度均为 \(1\) 的有向无环图,\(A\leq B\) 当且仅当存在从 \(A\) 向上到 \(B\) 的一条路径。
下图是 \(Z_2, Z_4\) 和 \(Z_8\) 的格。
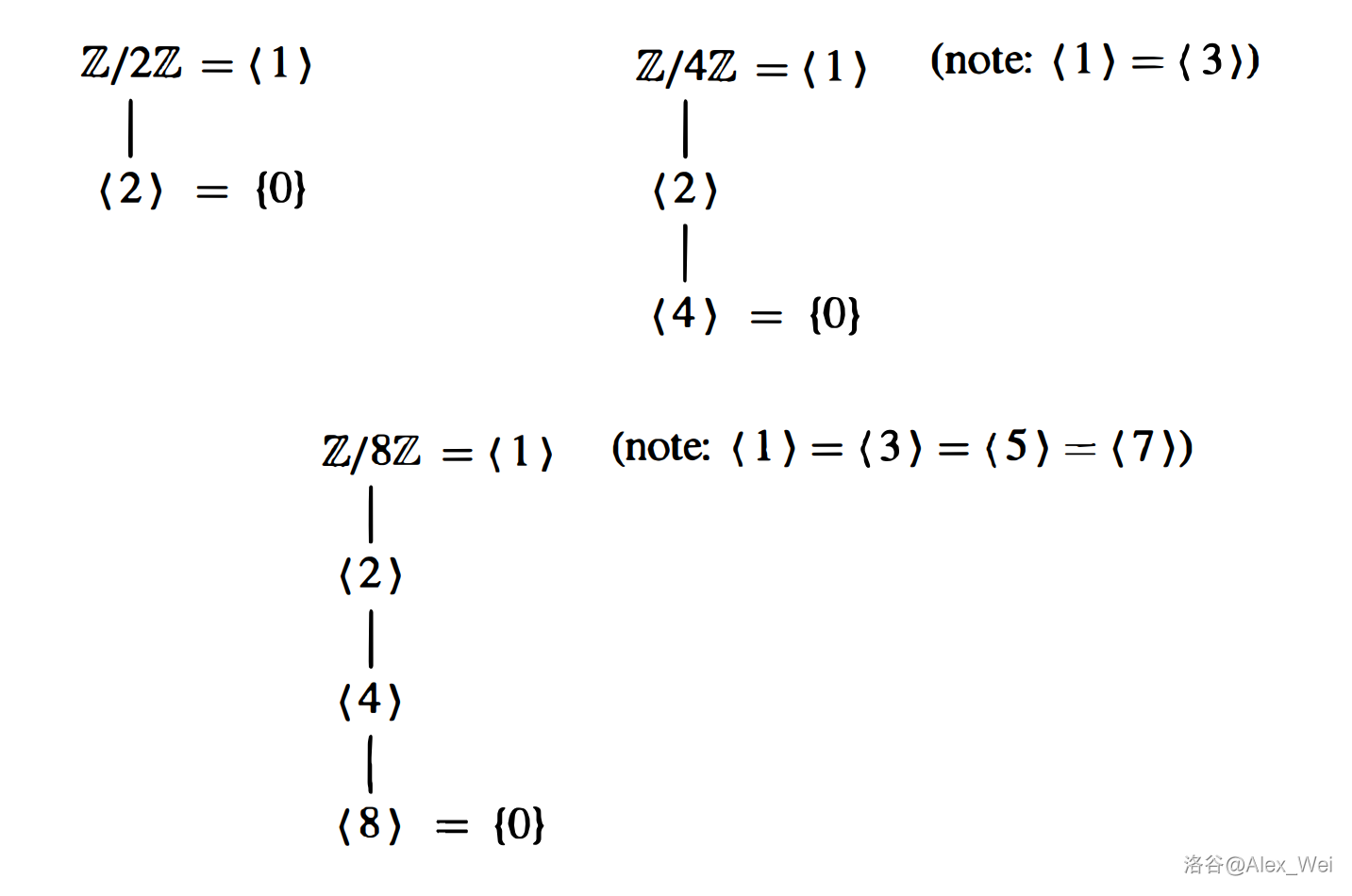
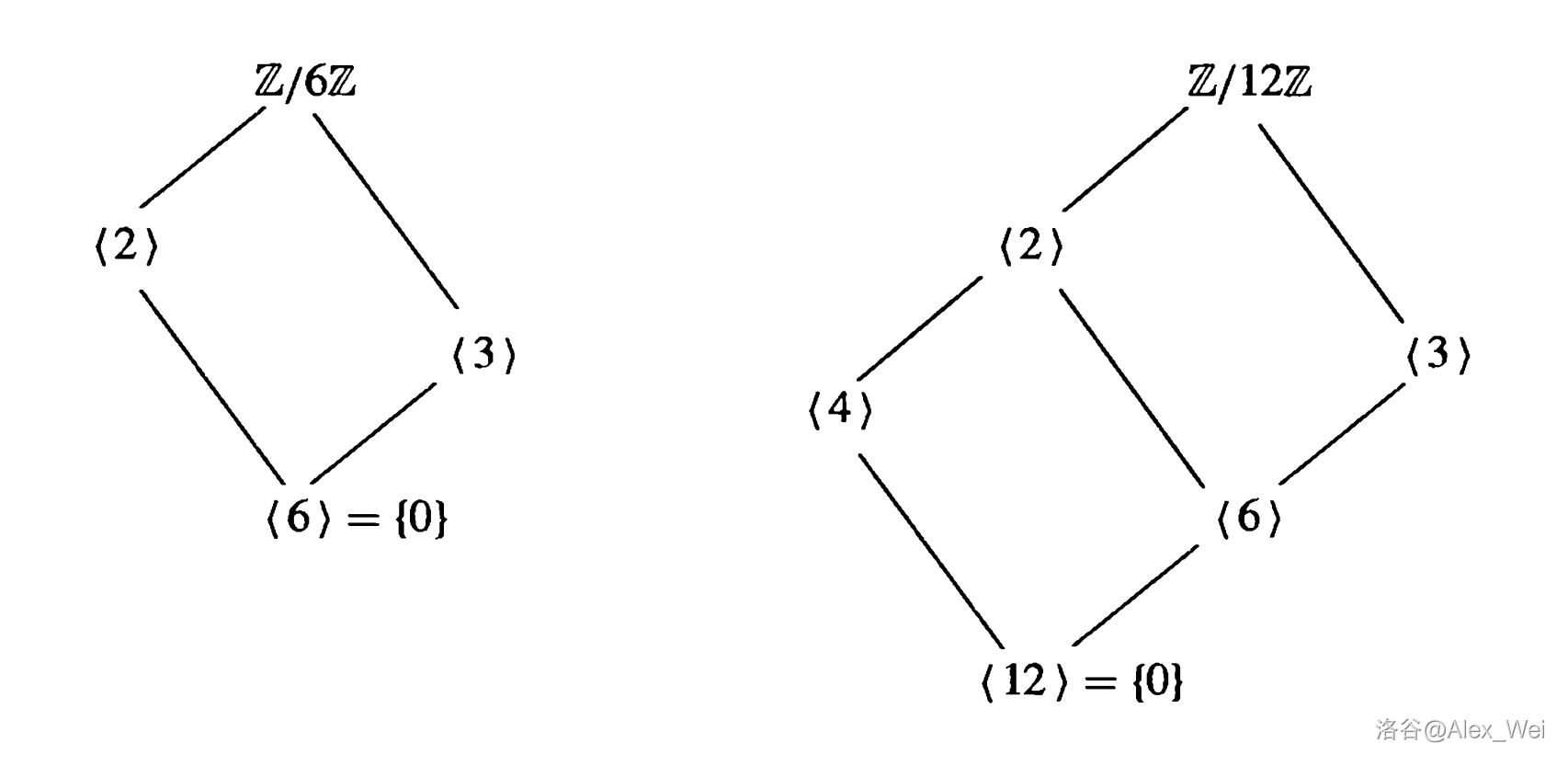
下图是 \(Z_6\) 和 \(Z_{12}\) 的格。
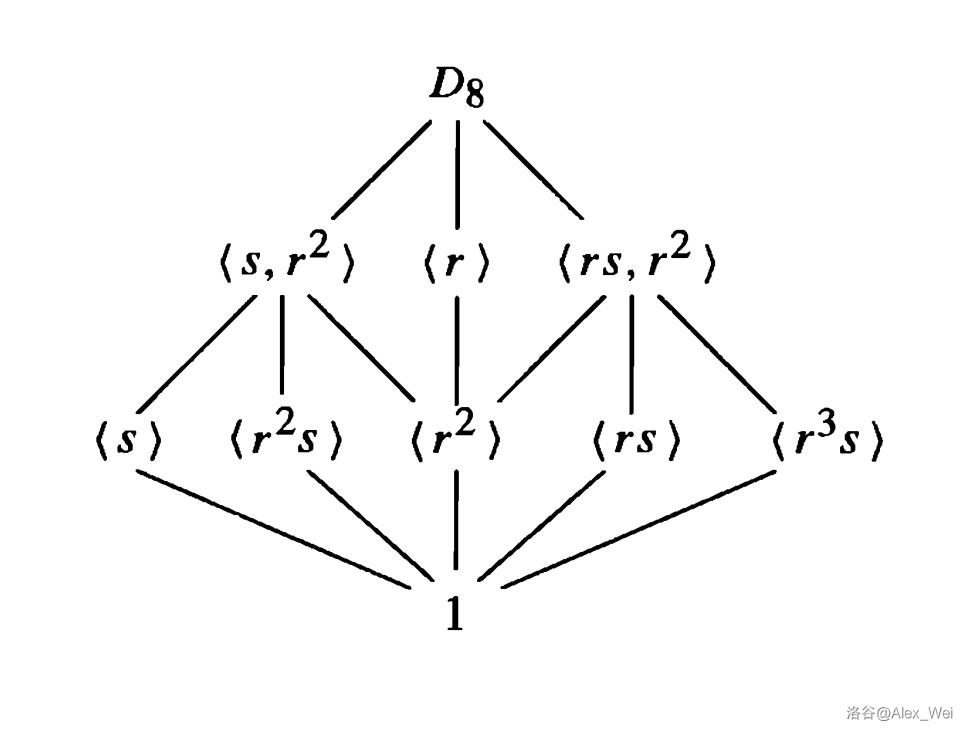
下图是 \(D_8\) 的格。
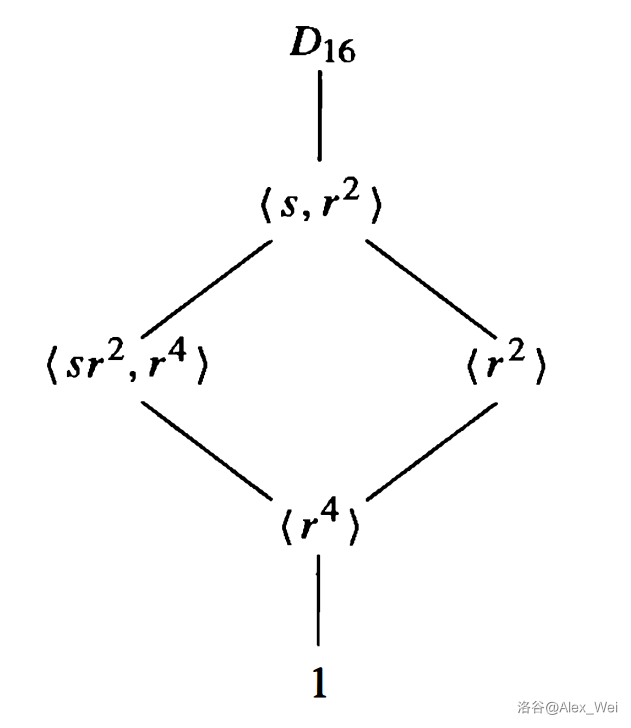
下图是 \(D_{16}\) 的格,它不是平面图。
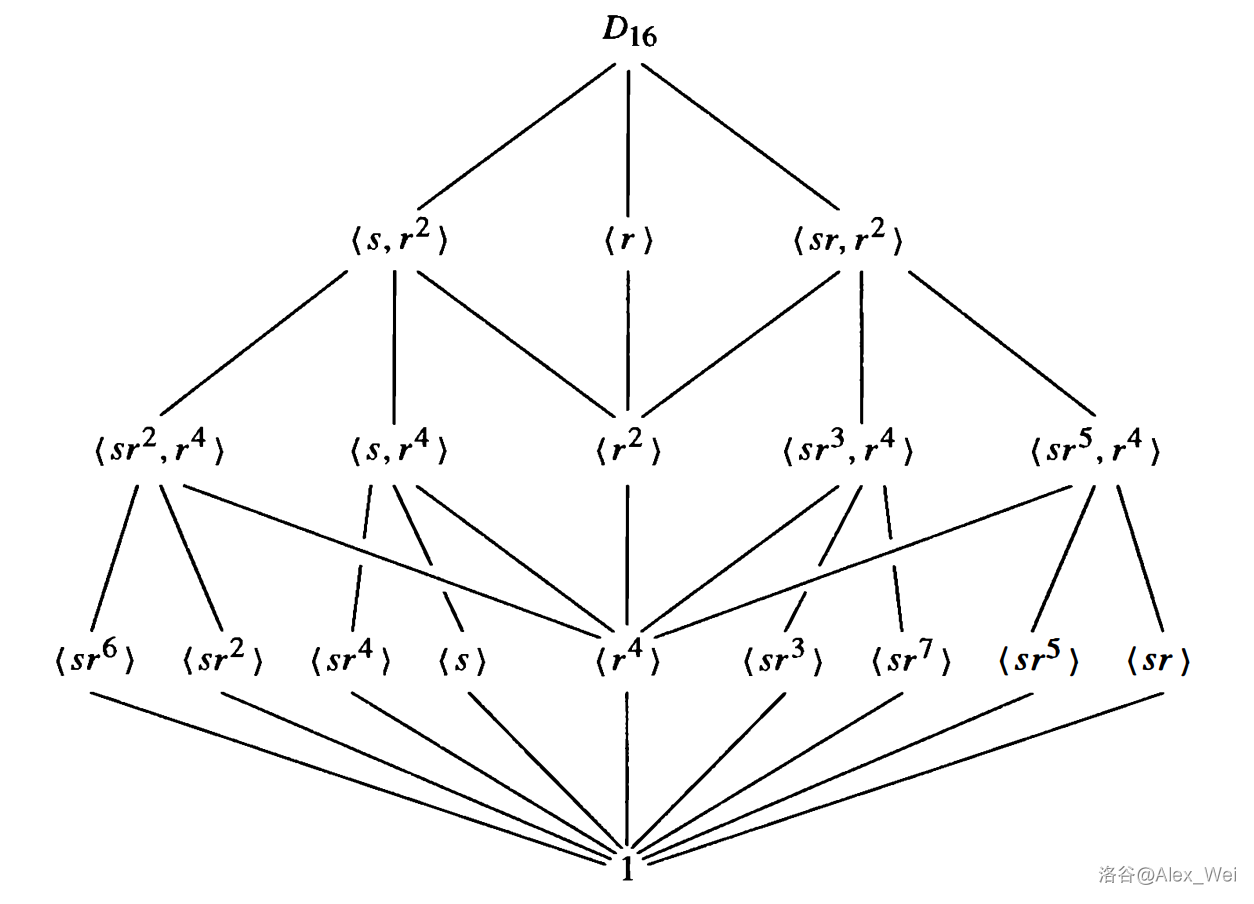
从格图可以直接读出若干子群的生成子群,也可以直接读出若干子群的交。
子格
大多数群的格比较复杂。只关心特定子群时,可以只画出相关部分,称为 子格(Sublattice)。
有点类似 OI 中的虚树。
下图是 \(D_{16}\) 的一个子格。