零、写在前面的话
我发现学习笔记是真的有必要的。很多比赛甚至做题的时候,学过的算法就出现在题目里面,然而我却忘记了之前对这个算法的深入理解,甚至忘了这个算法怎么打,更甚者,看不出来这个题目可以使用这种算法解决。
为了防止这种情况再度出现,我决定对自己的任何学过的算法写笔记,即使是低级的算法。同时,我会不定时翻看自己的笔记,笔记完全原创,希望留下更加深刻的印象。
一、线段树入门
1. 定义 & 作用
线段树是什么?一个可以用来维护许多区间操作的强大数据结构。它可以实现许多操作,例如区间加减乘除等。
2. 主要思想 & 实现
线段树,顾名思义,把一个序列分成很多个小线段。举个例子,有一个长度为 10 的序列,我们把它分成下面这个形状:
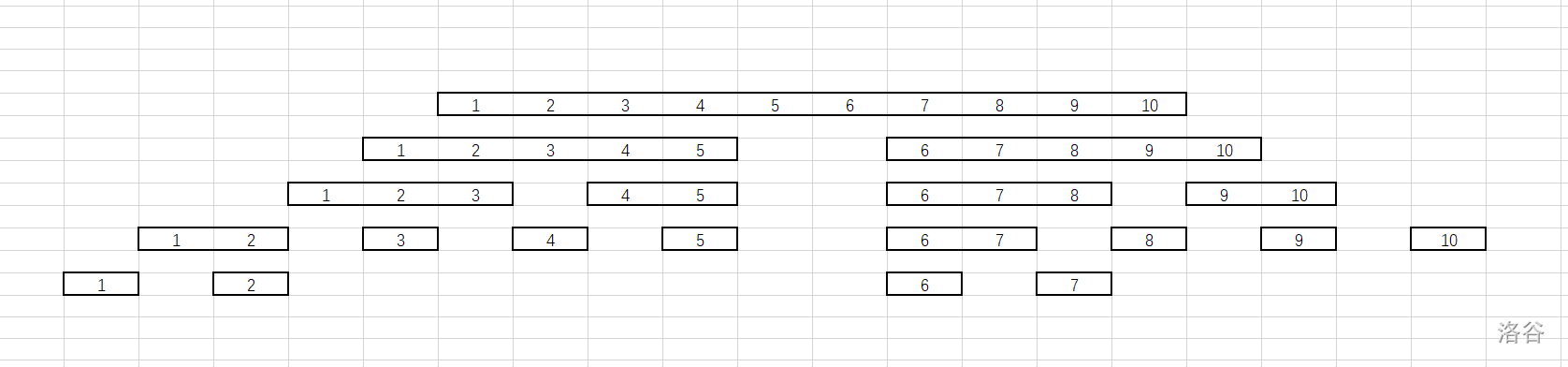
就是一直对半分下去,直到只有一个数。这时,许多操作就变得方便起来了。
2.1 查询
当我想查询一段数的和时,例如 3~7,我可以这么做:首先我把这个查询的任务交给区间 1~10,区间 1~10 进行处理后发现,有一段在他的左边,有一段在他的右边。于是,它交给它的左儿子区间一个任务:查询 3~5。再交给它的右儿子区间一个任务:查询 6~7,然后再把两段的和加起来就是答案,以此类推。当我发现我的区间被目标区间完全包含,就可以直接加上我这一段的值了。
于是,我们成功完成了区间查询操作。
2.2 单点修改
当我想修改一个数时,比如 4,我可以这么做:首先我把这个修改的任务交给区间 1~10,区间 1~10 进行处理后发现,4 在它的左儿子“管辖范围”内。于是,他把这个任务交给了左儿子 1~5,以此类推,直到找到 4 为止。
于是,我们成功完成了单点修改操作。
2.3 区间修改
这里需要讲到线段树的精髓了:lazytag,这个东西可以有很多的应用。我觉得,可以把这个东西理解为一个标记,一个支持区间修改的标记,而这个标记最常见的应用就是区间加。
首先,我们赋予每个区间一个值,称之为 lazytag。然后,在我想要区间修改时,找到我所需要的区间(像查询的方式),改变它的 lazytag 值以及存储的值。
重点来了,改变了之后,你什么也不需要做。没错,只需要改变一个值而不是你的区间中的每个数的值,也不需要改变你的子区间的值。
然后,当我们需要用到这个区间以及这个区间的子区间时(例如查询、修改时),我们再把 lazytag 的值“下放”。什么是下放呢?修改自己两个儿子的 lazytag 值,按照你的意愿。然后再修改两个儿子存储的值(它可能是最大值、和什么的)
于是,我们成功完成了区间修改操作。
二、线段树进阶
主要放一些例题,从中理解线段树的奥秘吧。
1. \(\color{#3498DB}\text{ P2146 [NOI2015] 软件包管理器}\)
树链剖分的模板题啊。这里用到的比较妙的一个是区间重置。把区间中的数设置为一个数。
附、模板
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=100010;
int n,a[N];
struct data
{
int data,l,r,lazy;
}tree[N*8];
void lazytag(int point)
{
if(tree[point].lazy)
{
int lson=point*2,rson=point*2+1,ly=tree[point].lazy;
tree[lson].data+=ly*(tree[lson].r-tree[lson].l+1);
tree[rson].data+=ly*(tree[rson].r-tree[rson].l+1);
tree[lson].lazy+=ly,tree[rson].lazy+=tree[point].lazy;
tree[point].lazy=0;
}
}
void build(int point,int l,int r)
{
if(point==1)
tree[point].l=1,tree[point].r=n;
else if(point%2==1)
{
tree[point].l=(tree[point/2].l+tree[point/2].r)/2+1;
tree[point].r=tree[point/2].r;
}
else
{
tree[point].l=tree[point/2].l;
tree[point].r=(tree[point/2].l+tree[point/2].r)/2;
}
if(tree[point].l>tree[point].r)return;
if(tree[point].l==tree[point].r)
{
tree[point].data=a[l];
return;
}
int mid=(l+r)/2;
build(point*2,l,mid);
build(point*2+1,mid+1,r);
int lson=point*2,rson=point*2+1;
tree[point].data=tree[lson].data+tree[rson].data;
}
void change(int point,int l,int r,int x)
{
if(l<=tree[point].l&&r>=tree[point].r)
{
tree[point].lazy+=x;
tree[point].data+=(tree[point].r-tree[point].l+1)*x;
return;
}
if(l>tree[point].r||r<tree[point].l)
return;
lazytag(point);
int mid=(l+r)/2;
if(l<=tree[point].l&&tree[point].r<=mid)
change(point*2,l,r,x);
else if(mid<=tree[point].l&&tree[point].r<=r)
change(point*2+1,l,r,x);
else
{
change(point*2,l,r,x);
change(point*2+1,l,r,x);
}
int lson=point*2,rson=point*2+1;
tree[point].data=tree[lson].data+tree[rson].data;
}
int ask(int point,int l,int r)
{
if(l<=tree[point].l&&r>=tree[point].r||l==r)
{
lazytag(point);
return tree[point].data;
}
if(l>tree[point].r||r<tree[point].l)
return 0;
lazytag(point);
int mid=(l+r)/2;
if(l<=tree[point].l&&tree[point].r<=mid)
return ask(point*2,l,r);
else if(mid<=tree[point].l&&tree[point].r<=r)
return ask(point*2+1,l,r);
else return ask(point*2,l,r)+ask(point*2+1,l,r);
}