常来看看。
Antiluna 好闪,拜谢 Antiluna。
1.奖金
每位参加会谈的代表提出了自己的意见:“我认为员工 a 的奖金应该比 b 高!”
Mr.Z 决定要找出一种奖金方案,满足各位代表的意见,且同时使得总奖金数最少。
每位员工奖金最少为 100 元,且必须是整数。
1 ≤ n ≤ 10000 ,1 ≤ m ≤ 20000。
对于每一个“\(a\) 的奖金应当大于 \(b\)”,在 \(a\) 与 \(b\) 之间建有向边然后跑一次拓扑,跑完之后可以发现,所有人的奖金应当会小于自己左边的任何一个人(为什么?考虑拓扑排序的例题,建边相当于代表了 \(a\) 应当在 \(b\) 的前面,所以奖金大的会在前面),所以从右往左循环(从 \(n\) 往 \(1\) 循环),对于每一个人,找到他所连向的每一条边然后更新自己这一条边的值。(因为要值最小所以加一就好了)。正确性证明:已知连向的边为奖金比自己小的,而比自己小的在自己的右边,所以已经更新过了。
int ans=0;
for(int i=n;i>=1;i--)
{
a[x[i]]=100;
for(int j=first[x[i]];j;j=e[j].next)
a[x[i]]=max(a[x[i]],a[e[j].to]+1);
ans+=a[x[i]];
}
cout<<ans;
2.送件
有一个邮递员要送东西,邮局在节点 1。他总共要送 n-1 样东西,
其目的地分别是节点 2 到节点 n。由于这个城市的交通比较繁忙,
因此所有的道路都是单行的,共有 m 条道路。这个邮递员每次只能带
一样东西,并且运送每件物品过后必须返回邮局。求送完这 n-1 样东
西并且最终回到邮局最少需要的时间。1 ≤ n ≤1000,1 ≤m≤100000
由于每一次送完都要回来,所以最短路为 \(\sum ^ n_{i=1}d_{1,i}+d_{i,1}\)(\(d_{i,j}\) 为 \(i\) 点到 \(j\) 点的最短路)。然而直接求 \(d\) 数组会超时,考虑使用单源最短路解决。\(d_{1,i}\) 实际上可以使用一次 dijk 解决,但是由于边为单向,所以 \(d_{i,j} ≠ d_{j,i}\)。因此现在需要求每一个点到 \(1\) 的最短路。只需要把边反着建再对 \(1\) 跑一遍 dijk 即可。(改变每一条边所指向的方向)。
3.比赛
N 头奶牛,编号 1∼N,一起参加比赛。奶牛的战斗力两两不同。
这些奶牛之间已经进行了 M 轮两两对决。在对决中,战斗力高的奶
牛一定会战胜战斗力低的奶牛。请问,通过上述 M 轮对决的结果,
可以确定多少头奶牛的具体战斗力排名。1≤N≤100 ,1≤M≤4500,
数据保证合法。
一眼拓扑,然而并不是。拓扑会错,因为拓扑排完之后依旧会有不确定性,依旧有可能不确定两个数之间的大小关系。考虑最短路解决,\(d_{i,j}=0/1\) 表示 \(i\) 能 \(/\) 不能战胜 \(j\)。转移可以使用 floyd 的枚举思想,枚举 \(k\)(中间奶牛)和 \(i\)、\(j\)(两端奶牛,需要求值的),由于当 \(a\) 战胜 \(b\),\(b\) 战胜 \(c\),\(a\) 肯定可以战胜 \(c\) 所以比赛具有传导性。于是这样转移:$ d_{i,j} |=d_{i,k} d_{k,j} $(即 \(d_{i,k}\) 为 \(1\) 且 \(d_{k,j}\) 为 \(1\) 时 \(d_{i,j}\) 为 \(1\))。最后统计,如果一头奶牛与其他所有奶牛的关系都已经确定(打的赢或打不赢),那么该奶牛的排名确定。
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
d[i][j]|=d[i][k]&d[k][j];
int ans=0;
for(int i=1;i<=n;i++)
{
bool p=true;
for(int j=1;j<=n;j++)
if(i!=j&&!d[i][j]&&!d[j][i])p=false;
ans+=p;
}
4.通信
某城市有 N 座通信基站,$P$ 条双向电缆,第 i 条电缆连接基站
Ai 和 Bi。特别地,1 号基站是通信公司的总站,N 号基站
位于一座农场中。现在,农场主希望对通信线路进行升级,其中升级第 i
条电缆需要花费 Li。电话公司正在举行优惠活动。农场主可以指定一条
从 $1$ 号基站到 N 号基站的路径,并指定路径上不超过 K 条电缆,
由电话公司免费提供升级服务。农场主只需要支付在该路径上剩余的电缆中,
升级价格最贵的那条电缆的花费即可。
可以发现,最终答案仅为一条边的边权,于是考虑二分答案这条边的边权。把所有大于当前二分的值的边权均设为 \(1\),其他设为 \(0\),跑 \(1\) 至 \(n\) 的最短路,答案小于等于 \(k\) 则代表当前值可行(可以找到一条路径,有不超过 \(k\) 个值大于它),移动 \(r\) 指针,否则代表不可行,移动 \(l\) 指针。
int l=0,r=L+1;
while(l<r)
{
int mid=(l+r)/2;
for(int i=1;i<=n;i++)
{
for(int j=first[i];j;j=e[j].next)
{
if(e[j].be>mid)e[j].v=1;
else e[j].v=0;
}
}
if(spfa())r=mid,p=true;
else l=mid+1;
}
5.排队
您刚刚在超市购物,然后前往结账。有两条队伍可用。第一个队伍目前有
len1 人,而第二个队伍有 len2 人。你想知道排在第一个队伍比排在
第二条队伍“好”(即更早轮到你)的概率。第一个队伍的收银员准备开始
给第一个队伍的第一个人结账。第二个队伍的收银员准备开始给第二个队伍
的第一个人结账。结账的时间取决于收银员的经验。
对于每对正整数(p,k):具有经验 p 的收银员将花费 k 秒来对任
何单个人结账的概率是:1/p*(1-1/p)^(k-1)。第一个队伍的收银员的经验
是 p1,第二个队伍的收银员的经验 p2。给出整数 len1,len2,p1 和 p2。
你想知道排在第一个队伍比排在第二条队伍“好”(即更早轮到你)的概率。
更确切地说,计算当前站在第一个队伍中的最后一个人比第二个队伍中的最后
一个人更早完成埋单的概率。
很好的思维题啊。我们将式子 \(((\frac{1}{p})\times(1 - \frac{1}{p})^{K-1})\) 换一种方式看:假设有 \(k\) 秒,每一秒收银成功地概率为 \(\frac{1}{p}\),那么失败的概率自然为 \(1-\frac{1}{p}\)。所以 dp,设 \(f_{i,j}\) 为第一条队伍走了 \(i\) 个人,第二条走了 \(j\) 个人时,第一条队伍好于第二条的概率。
转移方程于是显而易见了。有
\[f_{i,j}=f_{i-1,j}\times \frac{1}{p1}\times(1-\frac{1}{p2})+f_{i,j-1}\times (1-\frac{1}{p1})\times\frac{1}{p2}+f_{i-1,j-1}\times (1-\frac{1}{p1})\times(1-\frac{1}{p2})+f_{i,j}\times\frac{1}{p1}\times\frac{1}{p2} \]移项,变形,变成了
\[f_{i,j}\times(1-\frac{1}{p1}\times\frac{1}{p2})=f_{i-1,j}\times \frac{1}{p1}\times(1-\frac{1}{p2})+f_{i,j-1}\times (1-\frac{1}{p1})\times\frac{1}{p2}+f_{i-1,j-1}\times (1-\frac{1}{p1})\times(1-\frac{1}{p2}) \]于是去系数,有了
\[f_{i,j}=\frac{f_{i-1,j}\times \frac{1}{p1}\times(1-\frac{1}{p2})+f_{i,j-1}\times (1-\frac{1}{p1})\times\frac{1}{p2}+f_{i-1,j-1}\times (1-\frac{1}{p1})\times(1-\frac{1}{p2})}{(1-\frac{1}{p1}\times\frac{1}{p2})} \]问题得到了解决。感觉这是一个很好的 idea 啊。
double gt1=1.0/p1,gt2=1.0/p2;
double nt1=1-gt1,nt2=1-gt2;
for(int i=0;i<=l1;i++)
{
for(int j=0;j<=l2;j++)
{
if(j==0)f[i][j]=0;
else if(i==0)f[i][j]=1;
else
{
double res=0;
res+=f[i-1][j]*gt1*nt2;
res+=f[i][j-1]*nt1*gt2;
res+=f[i-1][j-1]*gt1*gt2;
f[i][j]=res/(1-nt1*nt2);
}
}
}
6.gold
Nosknah 喜欢收集宝藏,他知道学校的后花园里面藏有 P 个珍品。
经过严密调查,他知道后花园分成了 N 块区域,由 M 条无向路径连接。
Nosknah 要从 1 区域出发,捡完所有的宝藏后从 N 区域离开。他现在求助你:他最少要多少时间才能捡完宝藏并离开?
为了简化问题,我们假设 Nosknah 拿走珍品不需要花费任何时间。
先跑一次 floyd,求出每两个点之间的最短路。然后问题就可以看为一个简单的状压 dp 了。\(f_{i,j}\) 表示已经取完了二进制集合 \(i\) 以内的宝物,并且这一次取了宝物 \(j\) 时的最少用时。那么转移就显而易见了。
\[f_{i,j}=\min f_{j,k(k\in j,j\subset i)}+dis_{p_j,p_k} \]这题记下来主要是当时没想到吧。警醒一下自己,不是不会状压,而是看到数据老是不往状压那里想,输麻了。
for(int i=1;i<=(1<<p)-1;i++)
{
for(int j=1;j<=p;j++)
{
if(i&(1<<j-1))
{
if(i-(1<<j-1)==0)
f[i][j]=min(f[i][j],dis[1][a[j]]);
for(int k=1;k<=p;k++)
{
if((i-(1<<j-1))&(1<<k-1))
f[i][j]=min(f[i][j],f[i-(1<<j-1)][k]+dis[a[k]][a[j]]);
}
}
}
}
7.倍数
对于一个正整数 a 来说,它的各位数字之和就是它的价值,例如 a=133,
那么 a 的价值为 1+3+3=7。你需要找到一个价值最小的正整数 b, 且 b
是 k 的倍数, 输出满足条件的最小价值。
将每一个数看为节点,\(dis_i\) 表示除以 \(k\) 余数为 \(i\) 的最小价值。然后就简单了,先对 \(dis_{0\sim 9}\) 赋初值(\(dis_0\) 的初值为 \(k\)),然后可以使用 spfa,对于每一个数考虑在该数后面加上一个 \(0\sim 9\) 的每一条路径都考虑并且更新答案。
for(int i=0;i<=n;i++)
dis[i]=1145141919;
for(int i=0;i<=min(n,9);i++)
dis[i]=i,q.push(i);
dis[0]=n;
while(!q.empty())
{
int now=q.front();
vis[now]=0;
q.pop();
for(int i=0;i<=9;i++)
{
int ne=(now*10+i)%n;
if(dis[now]+i<dis[ne])
{
dis[ne]=dis[now]+i;
if(!vis[ne])
{
q.push(ne);
vis[ne]=1;
}
}
}
}
8.异闻带
好复杂啊。
有一棵树,n 个点,根为 1。有 m 个点为特殊点,有 q 个询问,每次割断一条
边(询问独立),问是否还能走到 1,能输出 yep,如果不能走到 1,输出最近
的特殊点距离,如果不能走到任何特殊点,输出 nop。
把问题分步解决~
第一步,判断能否到达 \(1\) 号节点。
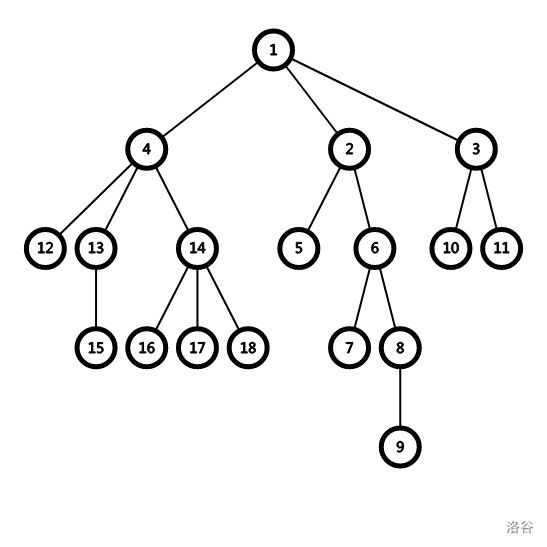
举个例子,割断了边 (\(2\),\(6\)),判断 \(8\) 号节点能否到达 \(1\) 号节点。设 \(1\) 号节点深度为 \(1\),那么 \(2\) 号深度为 \(2\),\(8\) 号深度为 \(4\)。使用倍增,从 \(8\) 号节点往上跳,跳到一个深度为 \(2\) 的节点后停止,判断这个节点是不是被割断的边中的一个端点。如果是,不能到达 \(1\) 号节点,否则可以到达。
第二步,找到最近的特殊点。
给上图加上边权吧。
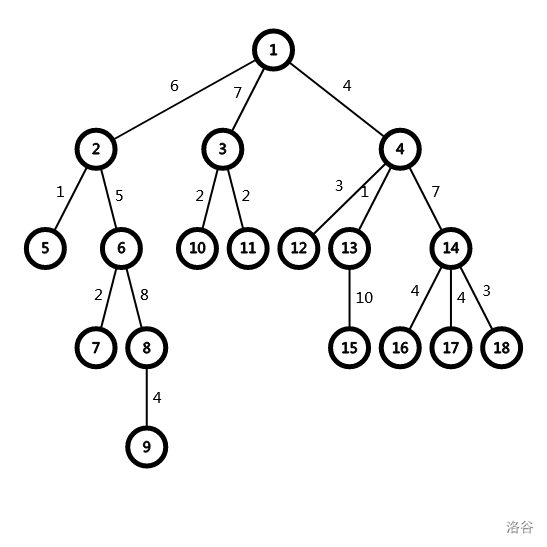
两个数组(均可以在预处理中求出),\(dis_x\) 和 \(f_x\)。设 \(dis_x\) 为 \(x\) 节点到 \(1\) 节点的距离,\(f_x\) 为 \(x\) 的子树中离 \(x\) 最近的特殊点距离。那么对于 \(x\) 节点来说,特殊点只会存在于两个地方:自己的子树中以及自己的祖先的子树中。所以距离节点 \(x\) 的最近特殊点为 \(\min f_y+dis_x-dis_y\)(\(y\) 为 \(x\) 的祖先)。将 \(dis_x\) 提取出来,变成了 \((\min f_y-dis_y)+dis_x\),把 \(f_y-dis_y\) 预处理出来。使用倍增或者是树链剖分解决这个问题。
代码还没写出来,不放了,以后补吧。
9.询问
没有场切,我忏悔,我忏悔。
有一个 n 个点,m 条边的无向联通图。每次一个询问,加入一条边,问这条边
会不会存在于新的最小生成树中。(询问之间独立)
水题 1h 没过,什么性质????
做法一:离线求问题的解。
直接将“询问中的边”与“原本就有的边”混为一谈,直接跑一次最小生成树,然后看“询问中的边”有没有出现在最终的最小生成树中。
做法二:倍增。
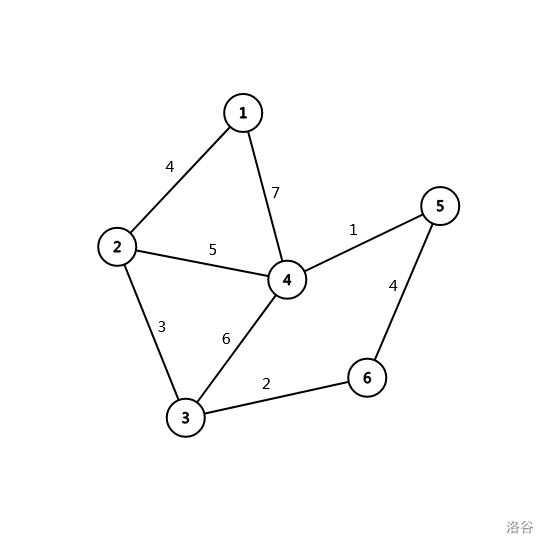
考虑在 Kruskal 中,为什么不能加入一条边?比如 \((2,4)\)。原因显然是加入这条边之后就会成环了。那么如何才能让这条边被加入呢?我们可以发现,加入 \((2,4)\) 之后的环是由 \((1,2)\)、\((1,4)\)、\((2,4)\) 组成的。因为 Kruskal 优先考虑边权小的边,所以只要让 \((2,4)\) 的边权不是最小就好了,那就需要求出 \((1,2)\)、\((1,4)\) 的边权最小值(在原本的最小生成树上求)。使用倍增即可。
代码简单就不贴了。
10.排列实验
给出包含n个元素的数组a[1..n],而且知道该数组保存的元素就是n的一个排
列。例如:[2,3,1,5,4]是5的一个排列。
[1,2,2]不是排列,因为2出现了两次。[1,3,4]不是排列,因为数组有3个元
素,但是数组里面出现了元素4。
现在依次进行m次实验,第i次实验的格式是这样的:给出Ri和Pi,表示对数组
a[1]至a[Ri]这一段数进行实验,实验有Pi的概率会成功,如果实验成功,那
么数组a[1]至a[Ri]会从小到大排好序;如果实验失败,那么数组a[1]至a[Ri]
不变。问依次进行完m次实验之后,数组a是升序数组的概率是多少。
显然,由于是一个排列,每一次把 \([1,r_i]\) 排序,那么前面的排序对后面的排序没有影响。我们需要一次可以直接一步到位的实验,这样的话,其他的成功或者失败就无所谓了。所以找出可以一步到位的实验,算出这些实验都不成功的概率,然后再用 \(1\) 减去这个概率就好了。
11.染色
有个R行C列的二维表格,行的编号从上往下是0至R-1,
列编号从左往右是0至C-1,二维表格共被分成R*C个单元格子。
每个单元格子一开始都是白色。
现在要执行K条指令,每条指令的步骤是:
(1) 随机从二维表格里选取一个单元格子(不妨称为A格子)
(2) 随机从二维表格里选取一个单元格子(不妨称为B格子)
(3) 格子A和B确定了一个矩形,矩形里面所有的单元格子都会被染色。
每个单元格随机选择,均匀分布,每个选择独立于其他选择。
A和B可能对应于同一个单元格。
你的任务是:执行K条指令后,有多少个单元格子会被染上颜色?输出该期望值。
简单题。但是自己没想出来。
为什么这么菜?为什么这么菜?为什么这么菜?为什么这么菜?为什么这么菜?为什么这么菜?为什么这么菜?为什么这么菜?为什么这么菜?为什么这么菜?
对于每一个格子,求出 \(k\) 次后都不被染色的概率(这一点只需要分类讨论,把避开当前格子的概率求出来),然后用 \(1\) 减去这个概率,再直接算期望值就好了。
12.玩具
在游戏开始之前,游戏大师在房间的某些地方隐藏了 N 个玩具。玩具编号为1到
N。您的任务是尽可能多地找到这些玩具。
你没有任何辅助信息就能找到第 i 个玩具的概率是 p[i]%。您每找到一个玩具
后,有可能可以得到一些辅助信息,这些辅助信息是告诉您其他某些玩具所在
的位置。如果您已经知道玩具的位置,您一定会找到它。
给出二维数组 clue[1..N][1..N],其中 clue[i][j]=‘Y’表示若找到第i个玩具
则会告诉您第 j 个玩具的具体位置;clue[i][j]=‘N’表示第i个玩具没有第j个
玩具位置的辅助信息;
你的任务是计算您在游戏中找到的玩具数量的期望值。
并查集也要用到啊。
把所有有关系的玩具放到一棵树中,也就是说这棵树中只要有一个玩具被找出,其他所有玩具都有了。所以算出每一颗树的所有玩具都无法被找到的概率,再用 \(1\) 减去这个概率求期望值就好了。
标签:p2,p1,frac,好题,笔记,times,学习,节点,dis From: https://www.cnblogs.com/WindChime/p/18127504