【学习笔记】并查集

标签：fa int 查集 笔记 学习 merge 转动 find

一、普通并查集

1. 定义 & 作用

并查集是管理元素分组的算法，可以高效对元素分组（合并为一组）以及查询两个元素是否在一组。

2. 主要思想 & 实现

对于每一个组，设置一个“组长”，每一次合并时只需要将其中一组的组长设为另一组的组长，查询时只需要查询组长是否相同。每一个组都可以理解为一个树形结构，树形结构的根即为我们要求的“组长”。求组长的时候可以递归实现，均摊时间复杂度为 \(O(\log n)\)。

然而有这样一句话：树总是有可能退化成链的。 因为链是树的一种形式，而一个并查集的结构显然有可能退化为一条链，这样每一次递归查询的时间就会退化为 \(O(n)\)。

考虑到上述情况优化，将形如：

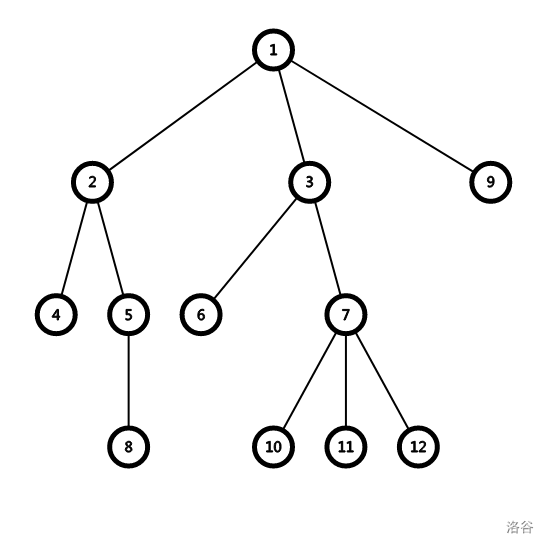
的树变为

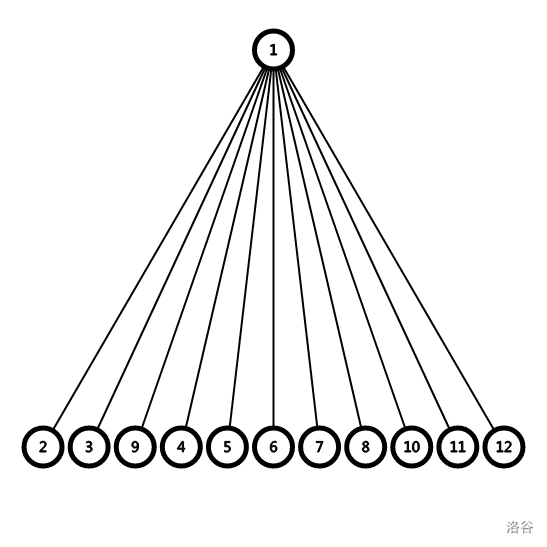
即所有的子节点直接连接根节点。那么有一个简单的实现方法：

原本的代码实现为：

int find(int x)
{
    if(fa[x]==x)
    	return x;
    return find(fa[x]);
}
//由递归实现查找函数

可以优化变为：

int find(int x)
{
    if(fa[x]==x)
    	return x;
    return fa[x]=find(fa[x]);
}
//由递归实现查找函数

此优化称路径压缩，通过减少树的高度让查找的时间变少。

二、带权并查集

1. 定义 & 作用

带权并查集，即为带有边权的并查集。

2. 思想 & 实现

均与并查集相同，但是合并时多了一项需要合并，即边权。带权并查集同样可以路径压缩。

有一点需要注意！带权并查集需要先递归查找再修改边权值。

三、拓展域并查集

1. 定义 & 作用

一般的并查集只能查找出各元素之间是否存在某一种相同的联系，如：\(a\) 和 \(b\) 是亲戚关系，\(b\) 和 \(c\) 是亲戚关系，这时就可以查找出 \(a\) 和 \(c\) 也存在亲戚关系。但如果存在多种相对的联系时一般的并查集就不行了，这时就需要对并查集进行拓展。即根据存在相对的关系数量把并查集的元素分出多份。

大概是，假设 \(a\) 与 \(b\) 是朋友，\(a\) 与 \(c\) 是敌人，那么可以查出 \(b\) 与 \(c\) 是敌人。假设 \(a\) 与 \(b\) 是敌人，\(a\) 与 \(c\) 是敌人，那么可以查出 \(b\) 与 \(c\) 是朋友。

2. 思想 & 实现

举个例子，假设存在“友好”与“敌对”两种关系，那么开一个大小为 \(n×2\) 的普通并查集。假设第 \(1\sim n\) 代表友好， \(n+1\sim n×2\) 代表敌对。那么当 \(a\) 与 \(b\) 友好，连接 \(a\) 与 \(b\)，再连接 \(a+n\) 与 \(b+n\)（连接 \(a\) 与 $b $ 代表两者是友好的；连接 \(a+n\) 与 \(b+n\) 代表 \(a\) 的敌人与 \(b\) 的敌人是友好的）。当 \(a\) 与 \(b\) 敌对，连接 \(a\) 与 \(b+n\)，再连接 \(a+n\) 与 \(b\)（敌人的敌人是朋友，连接 \(a\) 与 \(b +n\) 代表 \(a\) 与 \(b\) 的敌人友好；连接 \(a+n\) 与 \(b\) 代表 \(b\) 的与 \(a\) 的敌人是友好的）

首先，普通的操作还是一样的，只不过是空间需要两倍。

int fa[N*2];
int find(int x)
{
	if(x==fa[x])return x;
	return fa[x]=find(fa[x]);
}
void merge(int x,int y)
{
	fa[x]=find(y);
}

确定友好关系

	merge(x,y);
	merge(x+n,y+n);

确定敌对关系

	merge(x+n,y);
	merge(x,y+n);

查询关系

void ask(int x,int y)
{
	if(find(x)==find(y)&&find(x+n)==find(y+n))
    		cout<<"友好";
	if(find(x)==find(y+n)&&find(x)==find(y+n))
    		cout<<"敌对";
}

四、并查集例题

我选取了几道模板题自己 AC 了一下，写几个简短一点的题解吧。

1. \(\color{#3498DB}\text{P2024 [NOI2001] 食物链}\)

考虑这一题中有三种生物关系（同类，天敌，猎物），所以使用扩展域并查集，假设第 \(1\sim n\) 代表同类， \(n+1\sim n×2\) 代表天敌， \(n×2+1\sim n×3\) 代表猎物。有一点需要注意，\(a\) 的猎物的猎物，是 \(a\) 的天敌。（由于题目中提到的“环状”）

那么就有一个显然的做法了。

当 \(x\) 与 \(y\) 同类，做如下处理：

	merge(x,y);//x的同类是y的同类 
	merge(x+n,y+n);//x的天敌是y的天敌 
	merge(x+n+n,y+n+n);//x的猎物是y的猎物 

当 \(x\) 吃 \(y\)，做如下处理：

	merge(x+n,y);//x的猎物是y的同类 
	merge(x+n,y+n);//x的天敌是y的猎物（猎物的猎物是天敌） 
	merge(x,y+n+n);//x的同类是y的天敌 

然后就可以 AC 了。但值得一提的是，这题用带权并查集同样可以 AC，然而以我现在的水平暂时看不懂。所以挖个坑，以后回来填！

2. \(\color{#3498DB}\text{P4079 [SDOI2016] 齿轮}\)

很简单，只是题意不太好理解。大概是当一个齿轮转动一个角度之后，与它相连的齿轮要按照齿轮的转动比（每两个都不一样，由题目给出）（此后简称“齿转比”）转动。然后当一个一些齿轮的转动比不相容，齿轮就会卡住。问这些齿轮开始转动时会不会被卡住。

举个例子：

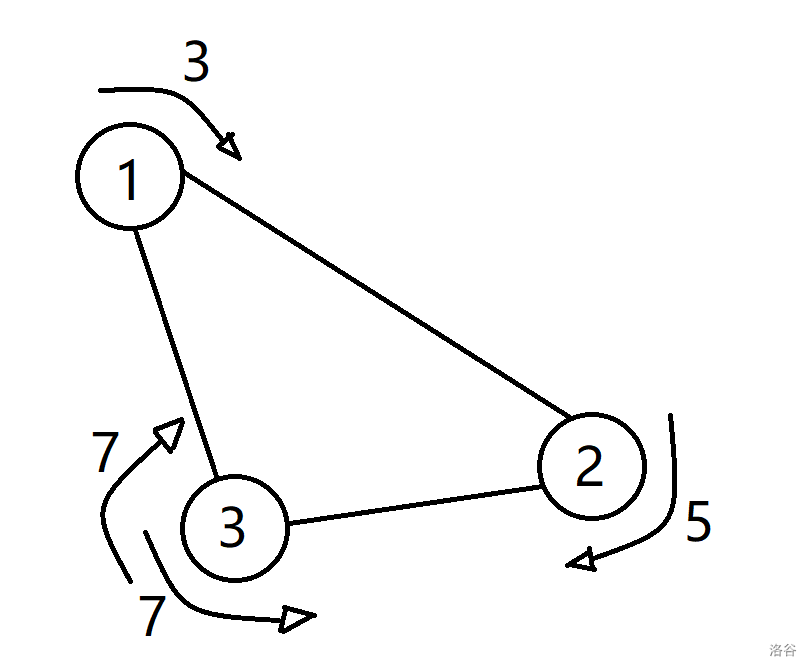
在这个例子中，\(1\) 号齿轮转动 \(3°\)，\(2\) 号会转动 \(5°\)，\(3\) 号会转送 \(-7°\)（因为 \(1\) 号转动引发 \(2\) 号按比例转动，\(2\) 号转动引发 \(3\) 号按比例转动）（可以将转动 \(-a\) 理解为逆时针旋转 \(a\)）。然而 \(1\) 号转动 \(3°\) 会直接导致 \(3\) 号转动 \(7°\)。（\(1\) 号与 \(3\) 号相连）

这时，\(3\) 号就需要同时转动 \(7°\) 与 \(-7°\)，而这显然行不通。

看到这里可以发现两个性质了：

• 将齿轮看作点，链条看作边，就会发现只有构成的图带有环才会有可能卡住。即，只要图中不包含环，一定不会卡住。

• 力之间具有传递性，\(a\) 到 \(b\) 的齿转比是 \(α\)，\(b\) 到 \(c\) 的齿转比是 \(β\)，那么 \(a\) 到 \(c\) 的齿转比是 \(αβ\)。

根据性质 \(2\) 推出另一个性质：

• 由于力的传递性，\(a\) 通过一系列的途中传递，传递到 \(b\) 的力会与原来的不同。而假设 \(a\) 与 \(b\) 是直接相连的，\(a\) 同时会直接给 \(b\) 传递一个力。而当这两个力不一样，齿轮就会卡住。

那么就有一个相对简单的做法了：对于每一条链，假设连接 \(a\) 与 \(b\)，做如下处理：

• 当 \(a\) 与 \(b\) 不处于一个树中，直接连接。
• 当 \(a\) 与 \(b\) 已经处于一个树中，设 \(a\) 到 \(b\) 的直接传导的力为 \(α\)，间接传导的力为 \(β\)，那么当 \(α ≠ β\)，该齿轮会卡住。

上述操作选择用带权并查集维护，然后就 AC 了，不过要注意一下精度问题。

具体的，设 \(f_i\) 代表 \(i\) 到 \(fa_i\) 的齿转比，则 \(i\) 到 \(j\) 的齿转比为 \(f_i ÷f_j\)，然后与它们的直接齿转比比较就好了。

3. \(\color{#3498DB}\text{P1682 过家家 }\)

用并查集维护女孩纸之间的关系，对于每一个当前女孩纸集合计算可以和他们玩的男孩纸，设第 \(i\) 个集合有 \(cnt_i\) 个男孩纸可以和他们玩，那么答案就是

\[ans=\min _{1\leq i\leq n}{cnt_i+k} \]

然而注意到最多只能玩 \(n\) 轮，所以最后答案实际是 \(\min ans,n\)

标签：fa,int,查集,笔记,学习,merge,转动,find
From： https://www.cnblogs.com/WindChime/p/18127523