0 前引
向量是一个在物理学中十分常见的概念,在数学和编程中的应用也很广泛。今天来浅谈一下向量的一些基本运算及其应用。
1 定义
向量是一个有方向,有长度的量,在坐标系中通常通过起点坐标和终点坐标表示。为了方便运算,七点坐标通常被设为原点。
但正如同刚才所说,向量的两个关键因素为方向和长度,所以还可以用这一种方式:
\[P = \{r, \alpha\} \]这也被称为 极角坐标系, \(r\) 也被称为向量的模长,\(\alpha\) 自然是与 \(x\) 轴成的夹角。
向量在坐标系中大致是这样:
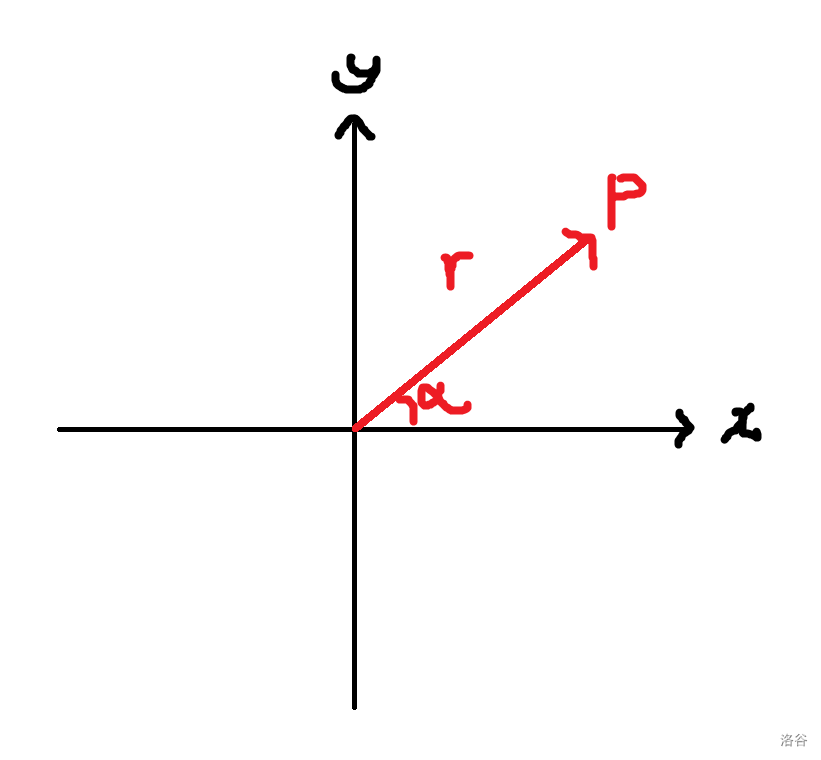
接下来来讲一些向量基本运算。
2 基本运算
2.1 向量加法
对于向量加法,我们考虑将两个向量移动到原点,然后这两个向量之和的向量的终点坐标就是:
\[(x_3, y_3) = (x_1 + x_2, y_1 + y_2) \]说白了,就是横坐标相加,纵坐标相加。
然后他的几何意义也不难。你可以把向量想成向一个方向移动一段距离。那么,他的图像如下:
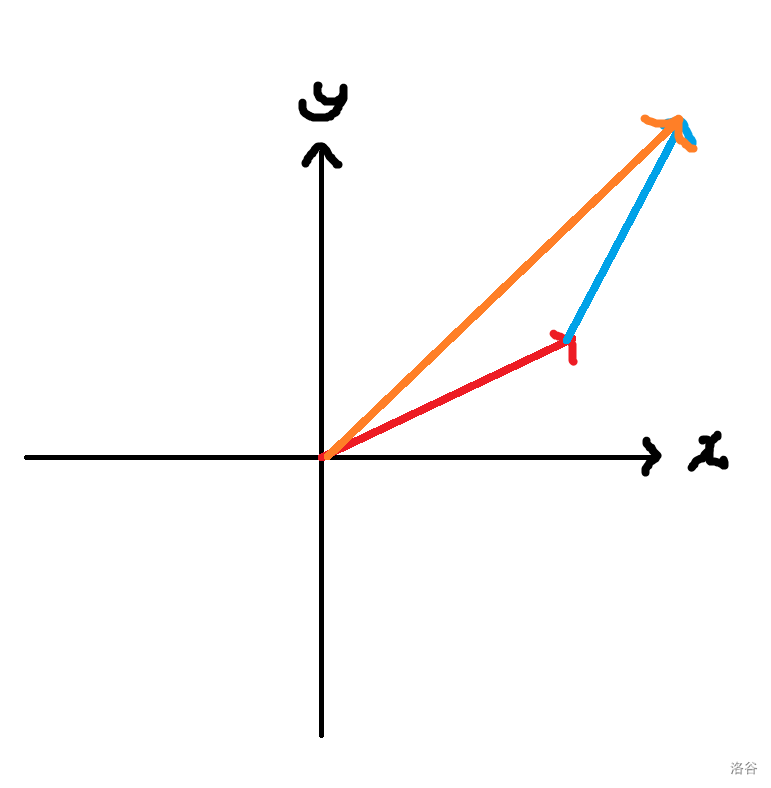
其实,它也可以表示成一个平行四边形的对角线,如图:
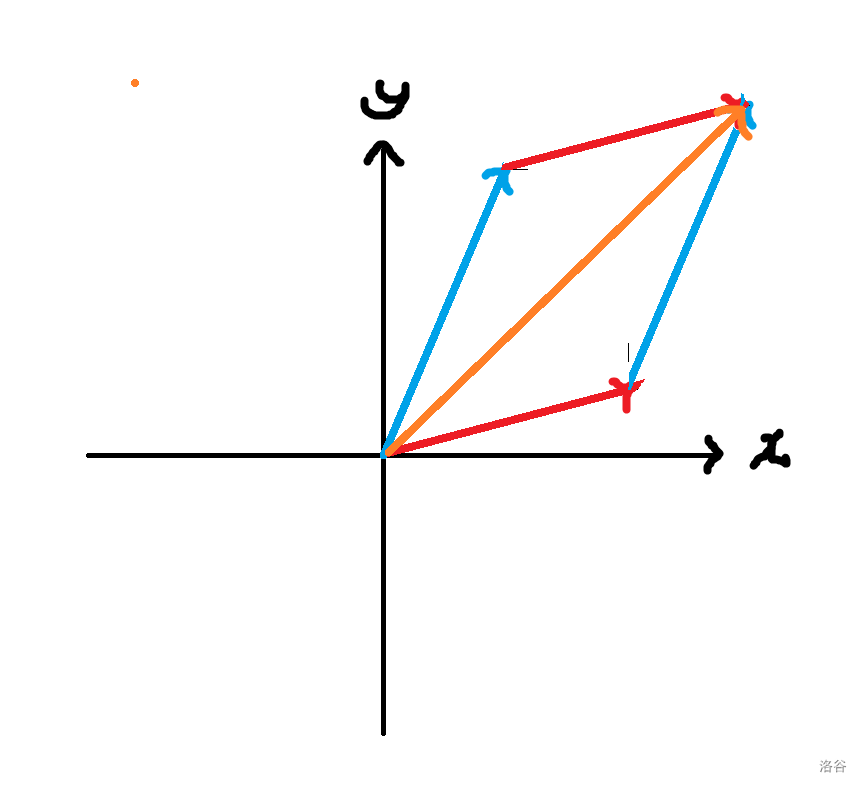
2.2 向量减法
我们已经知道了加法运算,那么可以考虑减法。
\[a - b = a + (-b) \]又知道相反数的定义为:向量的模不变,方向与之前相反
所以减法的图像就可以表示为:
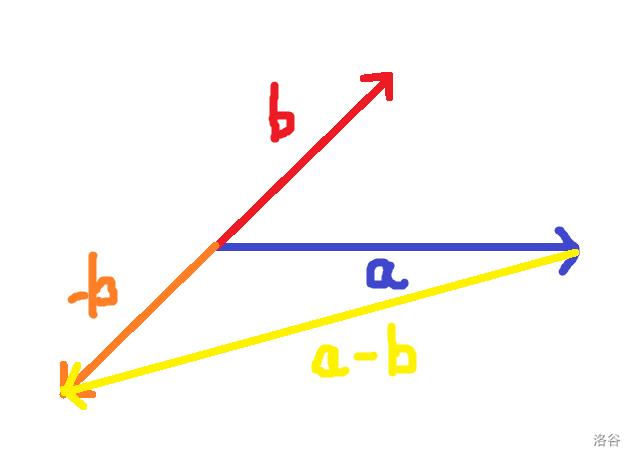
2.3 向量点乘
向量的点乘大小等于这两个向量的模的乘积再乘以两个向量之间的夹角的余弦,就是:
\[a \cdot b = \left\vert a \right\vert \left\vert b \right\vert \cos{<a,b>} \]当然,向量点乘还可以表示为:
\[a \cdot b = a_xb_x+a_yb_y+a_zb_z \]其实,两个向量 \(a\) 和 \(b\) 的点积的模等于 \(b\) 在 \(a\) 上的投影的向量乘以 \(a\) 的模,如图:

2.4 向量叉乘
严格来说,两个向量 \(a=x_1i+y_1j+z_1k,b=x_2i+y_2j+z_2k\) 的向量积是三维向量的二元运算,就是:
\[a \times b = \begin{vmatrix}i&j&k\\x_1&x_2&x_3\\x_2&y_2&z_2\end{vmatrix} =(y_1z_2-y_2z_1)i+(x_2z_1-x_1z_2)j+(x_1y_2-x_2y_1)k \]这个叉乘的模就是 \(a,b\) 作的平行四边形面积,方向可以用物理上的 右手螺旋定则 判断。其实,这个方向是与平行四边形所在的平面垂直的,如下图:
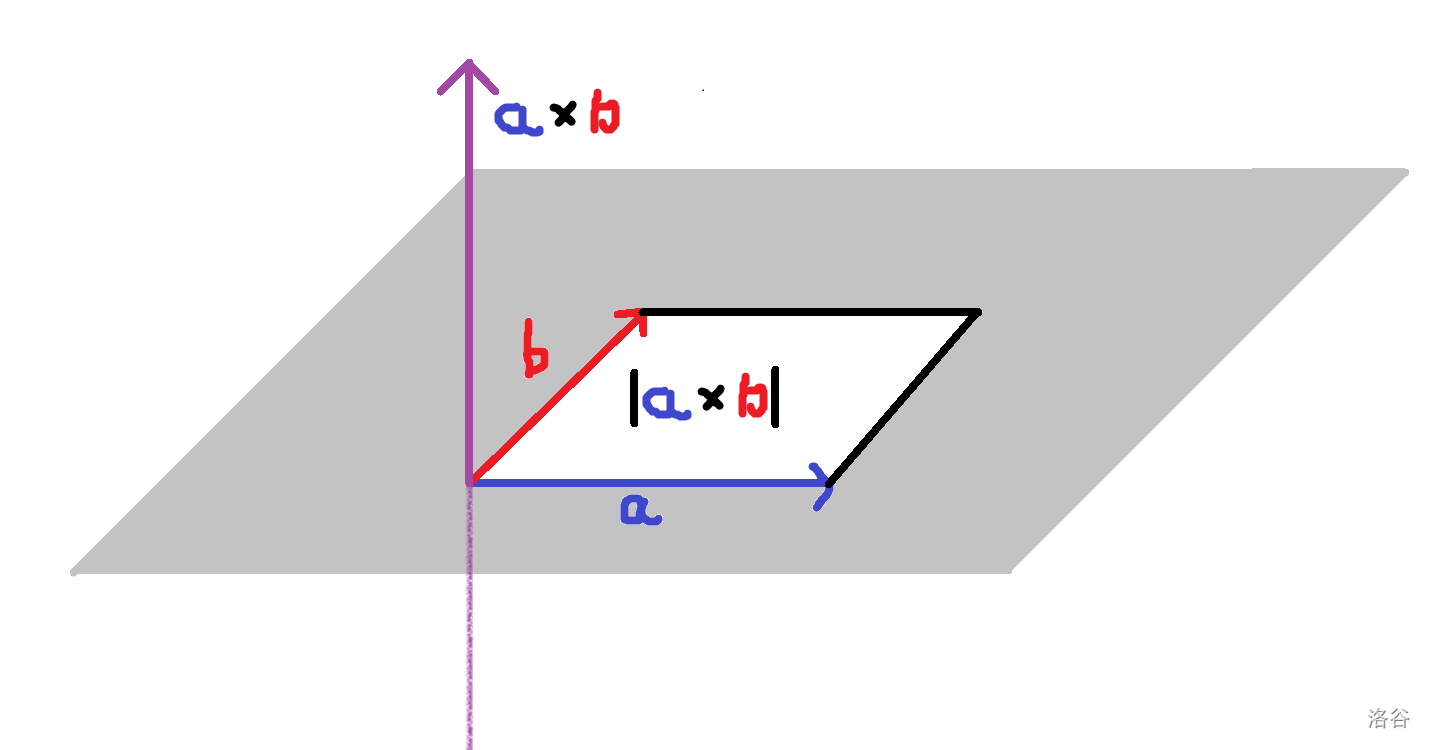
当然,还有一个更有用的公式,我们在应用的时候再细说。
3 运算应用
3.1 点乘的应用
点乘其实没啥应用的。
如果有三个点 \(P, Q, R\),并且 \(\overrightarrow{PQ}\) 与 \(\overrightarrow{PR}\) 同线,对于一个向量 \(\overrightarrow{PQ}\) 和一个点 \(R\),则:
- \(\overrightarrow{PQ} \cdot \overrightarrow{PR} < 0\),\(R\) 在 \(\overrightarrow{PQ}\) 的左手边。
- \(0 \leq \overrightarrow{PQ} \cdot \overrightarrow{PR} \leq \overrightarrow{PQ} \cdot \overrightarrow{PQ}\),则 \(R\) 在 \(\overrightarrow{PQ}\) 上。
- \(\overrightarrow{PQ} \cdot \overrightarrow{PQ} < \overrightarrow{PQ} \cdot \overrightarrow{PR}\),则 \(R\) 在 \(\overrightarrow{PQ}\) 的右手边。
同时,点乘性质非常多,如下:
- \(a \cdot e = \left\vert a \right\vert \left\vert b \right\vert \cos{<a,b>} = \left\vert a \right\vert \cos{<a,b>}\)
- \(a \perp b\) 等价于 \(a \cdot b = 0\),即 \(a_xb_x + a_yb_y + a_zb_z = 0\)
- 自乘:\(\left\vert a \right\vert ^ 2 = a \cdot a\)
- 结合律:\((\lambda \cdot a) \cdot b = \lambda(a \cdot b)\)
- 交换律:\(a \cdot b = b \cdot a\)
- 分配律:\(a \cdot (b + c) = a \cdot b + a \cdot c\)
3.2 叉乘的应用
叉乘还有另一个更有用的定义。把叉乘定义为一个矩阵的行列式:
\[p_1 \times p_2 = \det{\begin{vmatrix}x_1&x_2\\y_1&y_2\end{vmatrix}}=x_1y_2-x_2y_1=-p_2\times p_1 \]这时,如果 \(p_1 \times p_2 > 0\), 则相对于原点来说,\(p_1\) 在 \(p_2\) 的顺时针方向;如果 \(p_1 \times p_2 < 0\) 时,\(p_2\) 在 \(p_1\) 的顺时针方向;如果 \(p_1 \times p_2 = 0\),则 \(p_1\) 与 \(p_2\) 共线。
以上性质可以和 3.1 点乘的应用 相互结合,从而判断一个点与一个向量的位置关系。
4 题目分析
Atcoder Beginner Contest 296 G
其实,这道题我们可以考虑:对于每一个点,在它正下方的凸边形的边给快速求出来,然后计算这个点与这一条边的位置关系;同理,我们可以求出来此点正上方的边,然后计算位置关系。
然后,这个位置关系是什么?我们发现,在 3 运算应用 里,我们可以运用向量的叉乘与点乘,轻松的算出来点与向量的位置关系。那么,这道题就变成了一道大水题。
至此,这道题就结束了。
5 总结
向量真的很有用。
标签:PQ,overrightarrow,cdot,笔记,学习,right,向量,vert From: https://www.cnblogs.com/yh2021shx/p/18091080