P3338 [ZJOI2014] 力
给定数组 \(q\),有:
\[E_j=\sum\limits_{i=1}^{j-1}\frac{q_i}{(i-j)^2}-\sum\limits_{i=j+1}^{n}\frac{q_i}{(i-j)^2} \]求数组 \(E\)。
首先把数组从 \(0\) 开始编号。
然后如果有数组 \(g_i=\dfrac{1}{i^2}\),\(g_0=1\),我们发现:
\(E\) 的前半部分就是 \(q\) 和 \(g\) 卷积。
\(E\) 的后半部分就是 \(q\) 翻转后和 \(g\) 卷积。
由于是浮点数,直接上 FFT 卷积就行。
P5488 差分与前缀和
给定数组 \(a\),求 \(a\) 的 \(k\) 维前缀和或差分。
显然,每次让 \(a\) 和一个 \(n\) 项的数组 \(\begin{bmatrix}1&1&1&\dots &1\end{bmatrix}\) 卷积一下,就能求一次前缀和;
和 \(\begin{bmatrix}1&-1&0&\dots&0\end{bmatrix}\) 卷积就能求一次差分。
而卷积有交换律,所以我们只需要用多项式快速幂求出:\(\begin{bmatrix}1&1&1&\dots &1\end{bmatrix}^k\) 或 \(\begin{bmatrix}1&-1&0&\dots&0\end{bmatrix}^k\) ,然后再用 \(a\) 去卷一下就行了。
P3723 [AH2017/HNOI2017] 礼物
贺题解+抄同学思路,没有一点是自己想的。
给定两个长度为 \(n\) 的数组,可以对两数组其中之一进行两种操作:
- 整体加上一个非负整数 \(c\)。
- 把第一个放到最后面任意次。
你可以都做或者都不做。
问下式的最小值:
\[\sum\limits_{i=1}^{n}(a_i-b_i)^2 \]我们如果不限定正负,就可以考虑强制把 \(c\) 加在 \(a\) 上,于是原式变成:
\[\sum\limits_{i=1}^{n}(a_i+c-b_i)^2 \]推一下式子就是:
\[\sum a_i^2+\sum b_i^2+nc^2+2(\sum a_i-\sum b_i)c -2\sum a_i b_i \]显然当 \(c=\dfrac{-2(\sum a_i-\sum b_i)}{2n}=\dfrac{\sum b_i-\sum a_i}{n}\) 时取得最小值。
由于 \(c\) 可能加在 \(b\) 身上,我们可以把这种情况也讨论一下,具体到代码就是:
ll c1 = (ll)(((double)sb-(double)sa)/(double)n+0.5) ,c2 = (ll)(((double)sa-(double)sb)/(double)n+0.5);
c1 = c1*c1*n + 2 * (sa-sb) * c1;
c2 = c2*c2*n + 2 * (sb-sa) * c2;
res += min(c1,c2);
其中 \(sa=\sum a_i\),\(sb=\sum b_i\)。
由于当数组轮转时,只有 \(-2\sum a_ib_i\) 项在变,我们考虑这一项的最小值怎么求。
其实就是最大化 \(\sum a_i b_i\)。
我们考虑转化成卷积形式,即将 \(b\) 数组翻转,然后再复制两倍长接在自己后面,记为 \(b_{rev}\)。
我们将 \(a\) 和 \(b_{rev}\) 卷积,结果的 \(n\sim 2n-1\) 项中的最大值即为答案(编号从 \(0\) 开始)。

具体看这个图,就能明白卷积后 \(n\sim 2n-1\) 中的每一项都是一种轮换后的 \(\sum a_ib_i\) 的取值,于是取 \(\max\) 即可。
串串匹配相关
CF1334G Substring Search
给了一个排列,表达了每个字母可以映射成为另一个字母。
给了串 \(s\) 和串 \(t\),求 \(s\) 和每一个 \(t\) 的子串是否匹配。\(s\) 和一个串 \(t'\) 匹配,当且仅当 \(s_i=t'_i\) 或 \(s_i\) 所映射的字母与 \(t_i\) 相等。
对于两个字符,我们定义 \(S(a,b)=(a-b)^2(p_a-b)^2\),其中 \(p_a\) 是 \(a\) 所映射的字符。当 \(S(a,b)=0\) 时,\(a\) 这一位可以和 \(b\) 匹配。
所以对于 \(t\) 的某个子串 \(t'\),只要有:
\[\sum\limits_{i=1}^{\mid s\mid}S(s_i,t'_i)=0 \]那么 \(s\) 就能和 \(t'\) 匹配。
拆开 \(S(a,b)\)!
\[a^2p_a^2+a^2b^2+b^2p_a^2+b^4-2a^2p_ab-2ap_a^2b-2p_ab^3-2ab^3+4ap_ab^2 \]- \(a^2p_a^2\) 是定值。
- \(b^4\) 前缀和就行,\(O(1)\) 查询。
- \(-2a^2p_ab\),把 \(s\) 串翻转,分别以 \(a^2p_a\) 和 \(b\) 为系数卷积即可。
- \(-2ap_a^2b\),卷积即可。
- \(-2p_ab^3\),卷积即可。
- \(-2ab^3\),卷积即可。
- \(4ap_ab^2\),卷积即可。
- \(a^2b^2\),卷积即可。
- \(p_a^2b^2\),卷积即可。
当然,我们以 \(b\) 为主元,合并一下同类项:
\[b^4 + (-2a-2p_a)b^3+(4ap_a+a^2+p_a^2)b^2+(-2a^2p_a-2ap_a^2)b+a^2p_a^2 \]总而言之,卷积即可!
。。。逆天出题人卡 \(998244353\),于是我们给每个字符赋一个随机的权值,反正这个做法只要保证相同的字符权值相同就行,这样就能不被卡了!
CF528D Fuzzy Search
P4173 残缺的字符串
我曾经有一种 312 次 NTT 的做法,但这里时限太小常数太大,我写不下。
他敢给我开五秒,我就敢给你说这是正解。——Qcfff
嗯。我们忽略那种烧包做法。
还是字符串匹配,带个通配符。
还是构造一个字符间的匹配函数 \(S(s_i,t_j)\),要满足能匹配是 \(0\),不能匹配是正数。
可以这么构造(我孬子咧了愣是没想到):
\[S(s_i,t_j)=\Big(val(s_i)-val(t_j)\Big)^2val(s_i)val(t_j) \]然后我们令小写字母的 \(val()\) 价值函数互不相同,通配符的价值为 \(0\)。
跑一边就行了。
双倍经验:BZOJ4503. 两个串
P4199 万径人踪灭
这不乱写?——Qcfff
给定一个只有 \(\tt{a},\tt{b}\) 组成的紫狐汆 \(s\),求满足以下条件的子序列个数:
- 位置和字符都回文。
- 不连续
我们可以求出,以每个字符或每个空隙为回文中心,其左右有多少对回文字符对。
我们令 \(val({\tt a})=1\),\(val({\tt b})=2\)
然后考虑匹配函数:
\[S(a,b)=\Big(val(a)-val(n)\Big)^2val(a)val(b) \]是不是和上个题很像?我们用 \(s\) 串和它自己依照这个卷积,得到一个结果。先来张图:
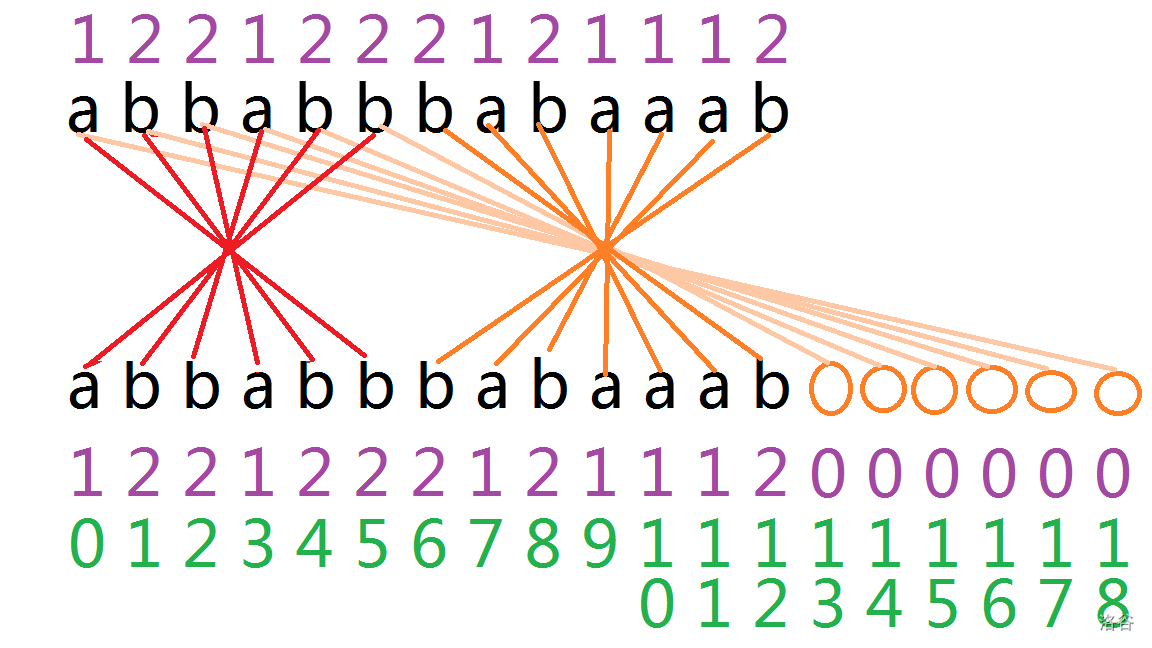
紫色字体表示权值,绿色字体代表编号。
我们保留这个卷积的前 \(2n\) 项,于是乎我们通过手玩,发现对于卷积结果的第 \(i\) 项,有:
-
若 \(i\) 为偶数,则这个卷积的结果代表了对称轴为 \(\dfrac{i}{2}\),左右两边不匹配的字符对个数的\(2\) 倍。
-
若 \(i\) 为奇数,则这个卷积的结果代表了对称轴为 \(\dfrac{i-1}{2}\) 和 \(\dfrac{i-1}{2}+1\) 之间的空隙,左右两边不匹配的字符对个数的\(2\) 倍。
这个图也刚好解释了我们为什么非要把 \(val(a)val(b)\) 乘进去,因为这样刚好可以把对称轴大于 \(\dfrac{n}{2}\) 的部分结果算出来。
然后我们对于每一个作为对称轴的位置,计算左右的总字符对对数减去卷积结果的 \(\dfrac{1}{2}\),就能算出对称轴为这个位置时,左右相等的对数,记为 \(v_i\big(i\in[0,2n)\big)\),这里 \(i\) 对应了一个对称轴,其对称轴上面解释过了。
接下来接着考虑原问题。不连续不好算,我们正难则反,考虑用无限制的减去连续的。
无限制的显然就是 \(\sum\limits_{i=0}^{2n-1}2^{v_i}-1\),表示对于每个位置作为对称轴时,其左右每一对都可以选或不选,再额外减去啥也不选的情况。
连续的话就是回文子串个数了,可以用 Manacher \(O(n)\) 算,也可以字符串哈希 \(O(n\log n)\) 算。后者好写就用了它。
图计数相关
关于图计数,有一个共同步骤:
设 \(f_i\) 表示 \(i\) 个节点的连通某图数量,其 EGF 为 \(\hat F(x)=\sum\limits_{i=0}\dfrac{f_ix^i}{i!}\)(\(f_0=0\))。
设 \(g_i\) 表示 \(i\) 个节点的某图数量,其 EGF 为 \(\hat G(x)=\sum\limits_{i=0}\dfrac{g_ix^i}{i!}\)(\(g_0=1\))。
我们有:
\[\mathrm{e}^{\hat F(x)}=\hat G(x) \]两边求 \(\ln\),有:
\[\hat F(x)=\ln \hat G(x) \]即为:连通的 \(\exp\) 的一般的,一般的 \(\ln\) 是连通的。
P4841 [集训队作业2013] 城市规划
抄题解。
求 \(n\) 个点无重边无自环有标号的无向连通图个数。
我们设 \(f_n\) 为上述数量。
\(g_n\) 为 \(n\) 个点无重边无自环有标号的无向图个数,也就是不保证联通。
考虑用两种方式表达 \(g_n\)。
首先直接想,从 \(n\) 个点中选出 \(2\) 个点,方案有 \(\dbinom{n}{2}\) 中,这每一组点之间的边都可连可不连,于是有:
\[g_n=2^{\binom{n}{2}} \]其次,考虑用 \(f\) 来表示 \(g_n\)。
我们考虑点 \(1\) 所在的连通块。枚举连通块大小为 \(i\)。
此时,从剩余的 \(n-1\) 个点中选出 \(i-1\) 个点,和 \(1\) 组成连通块,方案有 \(\dbinom{n-1}{i-1}\) 中;
这 \(i\) 个点在连通块里的方案数为 \(f_i\)。
而除去这 \(i\) 个点,剩余的 \(n-i\) 个点之间的无向图个数为 \(g_{n-i}\)。于是有:
\[g_n=\sum\limits_{i=1}^{n}\dbinom{n-1}{i-1}f_ig_{n-i} \]把 \(g\) 都写成第一种表达方式:
\[2^{\binom{n}{2}}=\sum\limits_{i=1}^{n}\binom{n-1}{i-1}f_i\cdot 2^{\binom{n-i}{2}} \]把组合数拆开,有:
\[2^{\binom{n}{2}}=\sum\limits_{i=1}^{n}\frac{(n-1)!}{(i-1)!(n-i)!}f_i\cdot 2^{\binom{n-i}{2}} \]左右同时除以 \((n-1)!\),有:
\[\frac{2^{\binom{n}{2}}}{(n-1)!}=\sum\limits_{i=1}^{n}\frac{f_i}{(i-1)!}\cdot\frac{2^{\binom{n-i}{2}}}{(n-i)!} \]这是个卷积的形式。具体地,我们设:
\[A(x)=\sum\limits_{i\ge 1}\frac{2^{\binom{i}{2}}}{(i-1)!}x^i,B(x)=\sum\limits_{i\ge1}\frac{f_i}{(i-1)!}x^i,C(x)=\sum\limits_{i=0}\frac{2^{\binom{i}{2}}}{i!} \]我们就有:
\[A(x)=B(x)C(x) \]于是:
\[B(x)=\frac{A(x)}{C(x)} \]多项式求逆即可。
还有另一种求法,就是用最开头提到的做法,令 \(g_i=2^{\binom{i}{2}}\),其 EGF:
\[\hat G(x)=\sum\limits_{i=0}\frac{2^{\binom{i}{2}}x^i}{i!} \]若答案的 EGF 为 \(\hat F(x)\),有:
\[\hat F(x)=\ln \hat G(x) \]于是多项式 \(\ln\) 即可。
P7364 有标号二分图计数
很不会做。遂题解抄之。(二分图啥性质忘光了)
首先题干没说二分连通图,意味着图可以不连通。
设有标号二分连通图的 EGF 为 \(\hat F(x)\),也就是说:
\[\hat F(x)=\sum\limits_{i=0}f_i\frac{x^i}{i!} \]其中 \(f_i\) 为有 \(i\) 个点的有标号二分连通图的个数。
我们要求的是有标号二分图,可以不连通。考虑其 EGF 为 \(\hat G(x)\)。于是根据开头提到的做法,有:
\[\hat G(x)=e^{\hat F(x)} \]我们发现 \(\hat F(x)\) 不好求,于是考虑另一种表达 \(\hat F(x)\) 的方式。
我们定义 \(n\) 个点的 “二分染色图” 个数为:\(n\) 个点的二分图(可以不连通)的个数,其中二分图进行了黑白染色。两个 “二分染色图” 不同,当且仅当边不同,或点的颜色不同。
考虑 “二分染色图” 的 EGF 为 \(\hat H(x)\)。我们用两种方式表达 \(H(x)\)。
- 考察其 \(\left[\dfrac{x^n}{n!}\right]\) 项系数 \(h_n\),表示由 \(n\) 个点组成的 “二分染色图” 的数量,有:
也就是把 \(n\) 个点分为两部分,一部分大小为 \(i\),全染成白色;另一部分大小为 \(n-i\),全染成黑色。这样划分的方案数为 \(\dbinom{n}{i}\);两部分之间任意一对点都可以选择连不连边,于是再乘上 \(2^{i(n-i)}\)。
- 想一想 \(\hat F(x)\) 和 \(\hat H(x)\) 的关系。
我们有:
\[\hat H(x)=\sum\limits_{i=0}\frac{2^i\hat F(x)^i}{i!}=e^{2x} \]\(m\) 个联通块的 “二分染色图” 个数的 EGF 为:\(\dfrac{2^{m}\hat F(x)^{m}}{m!}\),含义为每个联通块钦定一个颜色,有 \(2^m\) 中钦定方法;再把 \(\hat F(x)\) 通过 EGF 乘积的组合意义,组合起来,就得到了这个东西。
而我们枚举联通块个数,就得到了 \(\hat H(x)\) 的生成函数式子。
考察 \(\hat G(x)\) 与 \(\hat H(x)\) 的关系,有:
\[\hat G(x)=\sqrt{\hat H(x)} \]于是我们用第一种 \(\hat H(x)\) 的方式算出来 \(\hat H(x)\),再开个根就有了 \(\hat G(x)\)。
我们把 \(h_n\) 的式子搬过来,想想怎么预处理 \(H(x)\)。
\[h_n=\sum\limits_{i=0}^{n}\dbinom{n}{i}2^{i(n-i)} \]拆一下组合数,有:
\[h_n=n!\sum\limits_{i=0}^{n}\frac{1}{i!(n-i)!}2^{i(n-i)} \]然后这个 \(2^{i(n-i)}\) 很逆天。题解告诉我们:
\[i(n-i)=\dbinom{n}{2}-\dbinom{i}{2}-\dbinom {n-i}{2} \]什么含义呢?在 \(i\) 和 \(n-i\) 中分别选一个的方案数,等于在 \(n\) 个里面选两个,再减去两个都选在 \(i\) 里,和两个都选在 \(n-i\) 里的方案数。于是便有了这个式子。带回去:
\[h_n=n!\sum\limits_{i=0}^{n}\frac{1}{i!(n-i)!}2^{\binom{n}{2}-\binom{i}{2}-\binom {n-i}{2}} \]提出去一个 \(2^{\binom{n}{2}}\),里面的两个负指数扔到分母,有:
\[h_n=n!2^{\binom n2}\sum\limits_{i=0}^{n}\frac{1}{i!2^{\binom{i}{2}}}\cdot \frac{1}{(n-i)!2^{\binom {n-i}{2}}} \]就变成非常标志的卷积形式了!就能做了!
记得处理到 \(h_{2n}\),因为要开根。
P6295 有标号 DAG 计数
求 \(n\) 个点,有标号,弱连通的,DAG 图,的个数。
国家集训队2013年王迪的论文中,有讲到:
若 \(dp_i\) 表示不要求弱连通时 \(i\) 个点有标号的 DAG 图数量,令 \(dp_0=1\),有:
\[dp_i=\sum\limits_{j=1}^{i}(-1)^{j+1}dp_{i-j}\times2^{j(i-j)}\times\dbinom{i}{j} \]
(他原论文不是这么写的,我换了一下记号)
这个式子足够我们做出这个题:BZOJ2863. 愤怒的元首,甚至暴力卷积就行(除非你想要面对着 \(10^9+7\) 这毒瘤模数写 MTT)。提交记录
让我们回来写这个题。
too_later 这篇题解写的很清楚。
我们之前做二分图计数时有:
\[2^{j(i-j)}=2^{\binom{i}{2}-\binom{j}{2}-\binom{i-j}{2}} \]带进去,有:
\[dp_i=\sum\limits_{j=1}^{i}(-1)^{j+1}dp_{i-j}\times\frac{2^{\binom{i}{2}}}{2^{\binom{j}{2}}\cdot 2^{\binom{i-j}{2}}}\times\frac{i!}{j!(i-j)!} \]整理一下:
\[\frac{dp_i}{2^{\binom{i}{2}}i!}=\sum\limits_{j=1}^{i}\frac{(-1)^{j+1}}{2^{\binom{j}{2}}j!}\times\frac{dp_{i-j}}{2^{\binom{i-j}{2}}(i-j)!} \]我们令:
\[\begin{aligned} &f_i=\frac{dp_i}{2^{\binom{i}{2}}i!}\\ &g_i=\frac{(-1)^{i+1}}{2^{\binom{i}{2}}i!} \end{aligned}\]我们就有:
\[f_i=\sum\limits_{j=1}^{i}g_jf_{i-j} \]很像个卷积,但有些细节。我们首先把下界变成 \(0\):
\[f_i=\sum\limits_{j=0}^{i}g_jf_{i-j}-g_0f_i \]我们于是让 \(g_0=0\),就有:
\[f_i=\sum\limits_{j=0}^{i}g_jf_{i-j} \]很能卷了。但当我们 \(i=0\) 时,这个式子在表达:\(f_i=g_0f_0=0\),但我们把 \(i=0\) 带进 \(f_i\) 的定义式,发现显然错误。于是我们再填个补丁:
\[f_i=\sum\limits_{j=0}^{i}g_jf_{i-j} + [i=0] \]这个就完美了。如果 \(f,g\) 的 OGF 分别为 \(F(x),G(x)\),我们就有:
\[F(x)=F(x)G(x)+1 \]这个 \(+1\) 就是上面那个补丁在起作用。
解方程有:
\[F(x)=\frac{1}{1-G(x)} \]这样我们就能用 \(O(n\log n)\) 的复杂度,解决不要求弱连通的原问题了。
怎么变成连通呢?我们求出 \(F(x)\) 后就相当于求出了 \(f\) 的每一项。根据 \(f_i\) 的定义式,我们有:
\[dp_i=f_i\cdot 2^{\binom{i}{2}}\cdot i! \]我们写出 \(dp\) 的 EGF:
\[\hat F(x)=\sum\limits_{i=0}\frac{f_i\cdot 2^{\binom{i}{2}}\cdot i!x^i}{i!}=\sum\limits_{i=0}f_i\cdot 2^{\binom{i}{2}}x^i \]根据最开头提到的连通某图和某图的关系,设弱连通 DAG 图的 EGF 为 \(\hat H(x)\),有:
\[\hat H(x)=\ln \hat F(x) \]我们转成 EGF 后求一下 \(\ln\),就行了。
P5641 【CSGRound2】开拓者的卓识
对 Qcfff 的拙劣模仿。思路全是抄他的。
我们可以思考,\(a_i\) 对于 \(S_{k,1,r}\) 的贡献。
我们可以看做:在 \(1\sim i\) 中填 \(k\) 个左括号(可以填在一个位置上)的方案数为 \(L\),在 \(i\sim r\) 中填 \(k\) 个右括号(也可以填在一个位置上)的方案数为 \(R\);则 \(a_i\) 对 \(S_{k,1,r}\) 的贡献就是 \(a_i\cdot L\cdot R\)。
因为每个 \(S_{k-1,l,r}\) 只会对 \(\forall L\le l,R\ge r, S_{k,L,R}\) 产生贡献,所以上述结论是正确的。
我们蒙出结论:在长度为 \(len\) 的区间里填 \(k\) 个括号的方案为 \(C_{k+len-1}^{k}\),为什么不知道,但这个是 \(\begin{bmatrix}1&1&\dots&1\end{bmatrix}\) 的 \(k\) 维前缀和的第 \(len\) 项绝对没错,手玩一下 \(len=5,k=3\) 就能明白。但为什么就是这个组合数?刷到的朋友救一下!
于是我们就可以写出一个东西:
\[S_{k,1,r}=\sum\limits_{i=1}^{r}a_i\cdot C_{k+i-1}^{k}\cdot C_{k+r-i}^{k} \]我们发现一共需要的组合数为 \(C_{k}^{k},C_{k+1}^{k},\dots,C_{k+n-1}^{k}\),这些显然可以 \(O(n)\) 预处理。即:
\[C_{k+i}^{k}=\frac{C_{k+i-1}^{k}\cdot (k+i)}{i} \]然后我们计算出
\[f=\begin{bmatrix}C_{k}^{k}a_1&C_{k+1}^{k}a_2&\dots&C_{k+n-1}^{k}a_n\end{bmatrix} \]和
\[g=\begin{bmatrix}C_{k}^{k}&C_{k+1}^{k}&\dots&C_{k+n-1}^{k}\end{bmatrix} \]通过手玩小样例,发现答案就是 \(f\) 和 \(g\) 的卷积。ntt 即可。
关于为什么有那个组合数的结论,我们这里来证明一下。
原问题可以理解为:有 \(k\) 个球,放进 \(len\) 个盒子里,盒子里可以放多个球,可以空盒子,求方案数。
可以进一步理解为:方程 \(x_1+x_2+\dots +x_{len}=k\) 的非负整数解的组数。
进一步理解为:方程 \(x_1+x_2+\dots +x_{len}=k+len\) 的正整数解的组数。
我们可以看成在 \(k+len-1\) 个空隙中插入 \(len-1\) 个隔板,隔板把球分成了 \(len\) 组,每组就是一个 \(x\) 的解。
所以方案数就是 \(C_{k+len-1}^{len-1}=C_{k+len-1}^{k}\)。证毕。
UVA12298 Super Poker II
有一副扑克,四种花色,点数只能是合数。每种牌都有无限种。有 \(n\) 中牌丢失了,你需要求出四种花色的牌各用一张,拼成 \(a\sim b\) 内每个数的方案数。
我们考虑构造四个数列 \(p_1\sim p_4\),分别代表四种花色。
对于 \(p_i\) 的每一项 \(p_{i,j}\),如果满足下列三个条件就赋值为 \(1\):
- \(j\le b\)
- \(j\) 为合数
- 花色为 \(i\),点数为 \(j\) 的这张牌没有丢失
其它位置赋值为 \(0\)。
我们考虑 \(p_i\) 和 \(p_j\) 两序列卷积的意义。不难发现卷积后 \([x^n](p_i\times p_j)\) 代表的意义就是各用一张花色为 \(i\) 和 \(j\),拼成 \(n\) 的方案数。
于是我们把 \(p_1\sim p_4\) 卷起来就行了。
注意这题要用 long double 的 FFT,多测不清空,爆零两行泪。
CF1548C The Three Little Pigs
显然答案为 \(\sum\limits_{j=0}^{n}\dbinom{3j}{x}\)。多次询问,联想生成函数,我们构造出 OGF:
\[F(x)=\sum\limits_{n=0}x^n\sum\limits_{j=0}^{n}\dbinom{3j}{i} \]然后很神奇地,更换枚举顺序,有:
\[\sum\limits_{j=0}^{n}\sum\limits_{n=0}\dbinom{3j}{i}x^i \]后面的东西有封闭形式:
\[\sum\limits_{j=0}^{n}(x+1)^{3j} \]这个整体,通过错位相减,也能求出封闭形式为:
\[F(x)=\frac{(x+1)^{3n+3}-1}{(x+1)^3-1} \]理论上来说可以做了。直接暴力跑大除法!
CF1251F Red-White Fence
不会做,抄了题解。
我们发现 \(k\),即红栅栏的个数很小。于是我们考虑预处理出:对于每个红栅栏,其左右一共放 \(i\) 个白栅栏有多少种方案。
我们拿其中一个来距离。设 \(f_{i,j}\) 为一共用 \(i\) 个白栅栏,所用的白栅栏高度均 \(\le j\) 的方案数字
发现一种高度的白栅栏只有三种有用的情况:
- 没有
- 只有一个
- 至少两个
我们分别考虑每种情况如何转移
-
高度为 \(j\) 的白栅栏没有,此时 \(f_{i,j}=f_{i,j-1}\)。
-
高度为 \(j\) 的白栅栏只有一个,此时 \(f_{i,j}=f_{i,j-1}+2f_{i-1,j-1}\),即要么不用这个栅栏,要么用它,放左边或放右边共两种情况,故乘以 \(2\)。
-
高度为 \(j\) 的白栅栏有至少两个,此时 \(f_{i,j}=f_{i,j-1} + 2f_{i-1,j-1} + f_{i-2,j-1}\),即要么不用它,要么只用一个,放左放右各一种所以乘以 \(2\),要么两个都用上,必须左右都放所以只乘 \(1\)。
我们发现第一种情况相当于什么也不做,第二种情况相当于给原来的 \(f\) 数组卷上 \(2x+1\),第三种情况相当于给原来的 \(f\) 数组卷上 \((x^2+2x+1)\),所以我们设第二种情况的栅栏共有 \(x_1\) 个,第三种情况的栅栏共有 \(x_2\) 个,于是我们索求的 \(f\) 数组即为:
\[(2x+1)^{x_1}(x^2+2x+1)^{x_2}=(2x+1)^{x_1}(x+1)^{2x_2} \]对左右分别用二项式定理算系数,然后 NTT 卷积到一起就行了。
P4091 [HEOI2016/TJOI2016] 求和
给出 \(n\),求:
\[\sum\limits_{i=0}^{n}\sum\limits_{j=0}^{i}\begin{Bmatrix}i\\j\end{Bmatrix}2^j\cdot j! \]我们知道第二类斯特林数有通项公式。
带进去,有:
\[\sum\limits_{i=0}^{n}\sum\limits_{j=0}^{i}\sum\limits_{k=0}^{j}\frac{(-1)^{j-k}k^i}{k!\cdot(j-k)!}2^j\cdot j! \]我们发现和 \(i\) 有关的只有一项 \(k^i\),于是我们孤立它,更换枚举顺序,把 \(j,k\) 提到前头:
\[\sum\limits_{j=0}^{n}\sum\limits_{k=0}^{j}\frac{(-1)^{j-k}}{k!\cdot(j-k)!}2^j\cdot j! \sum\limits_{i=j}^{n}k^i \]然后我们发现后面那一项就是:
\[\sum\limits_{i=j}^{k}=\frac{k^{n+1}-k^j}{k-1} \]带回去,有:
\[\sum\limits_{j=0}^{n}\sum\limits_{k=0}^{j}\frac{(-1)^{j-k}}{k!\cdot(j-k)!}2^j\cdot j! \frac{k^{n+1}-k^j}{k-1} \]整理整理,为:
\[\sum\limits_{j=0}^{n}2^j\cdot j!\sum\limits_{k=0}^{j} \frac{k^{n+1}-k^j}{k!(k-1)}\cdot \frac{(-1)^{j-k}}{(j-k)!} \]发现很像一个卷积,我们把 \(k^{n+1}-k^j\) 拆开:
\[\sum\limits_{j=0}^{n}2^j\cdot j!\Bigg(\sum\limits_{k=0}^{j} \frac{k^{n+1}}{k!(k-1)}\cdot \frac{(-1)^{j-k}}{(j-k)!} - \sum\limits_{k=0}^{j} \frac{k^j}{k!(k-1)}\cdot \frac{(-1)^{j-k}}{(j-k)!}\Bigg) \]发现前面一坨可以卷积,但后面一坨???
我们相当于在求这玩意:
\[\sum\limits_{j=0}^{i}A_jB_{i-j}j^i \]卷个毛。卷不了。我超不会推了????
拜 Qcfff 所赐,我们把原式子放出来:
\[\sum\limits_{i=0}^{n}\sum\limits_{j=0}^{i}\begin{Bmatrix}i\\j\end{Bmatrix}2^j\cdot j! \]我们发现,\(j\) 的上界完全可以变成 \(n\)。然后呢?我们和之前一样推一遍式子。直到孤立 \(i\) 那一步,我们发现了:
\[\sum\limits_{j=0}^{n}\sum\limits_{k=0}^{j}\frac{(-1)^{j-k}}{k!\cdot(j-k)!}2^j\cdot j! \sum\limits_{i=0}^{n}k^i \]我们 \(i\) 的下界限制 \(j\) 被解除了!!!!!这意味着我们后面的东西变成了:
\[\sum\limits_{i=j}^{k}=\frac{k^{n+1}-1}{k-1} \]该死的 \(k^j\) 项死掉了!!!它死了哈哈哈哈哈哈哈哈哈哈哈哈
然后我们接着推:
\[\sum\limits_{j=0}^{n}2^j\cdot j!\sum\limits_{k=0}^{j} \frac{k^{n+1}-1}{k!(k-1)}\cdot \frac{(-1)^{j-k}}{(j-k)!} \]这个东西就能直接卷积了。欲哭无泪。
注意有好几个实现细节:
- \(0^0=1\)。
- 特殊注意一下 \(k=1\) 时,\(\sum\limits_{i=0}^{n}k^i=n+1\)。
没了
最后大力膜拜 Qcfff 佬!!!
P3711 仓鼠的数学题
求:
\[\sum\limits_{k=0}^{n}a_k\sum\limits_{i=0}^{x}i^k \]我们有:
\[\sum\limits_{i=0}^{n}i^k=n^k + \frac{1}{k+1}\sum\limits_{i=0}^{k}\binom{k+1}{i}B_in^{k+1-i} \]带进式子里,有:
\[\sum\limits_{k=0}^{n}a_k\Bigg(x^k + \frac{1}{k+1}\sum\limits_{i=0}^{k}\binom{k+1}{i}B_ix^{k+1-i}\Bigg) \]拆个括号:
\[\begin{aligned}&\sum\limits_{k=0}^{n}a_kx^k+\\&\sum\limits_{k=0}^{n}a_k\Bigg( \frac{1}{k+1}\sum\limits_{i=0}^{k}\binom{k+1}{i}B_ix^{k+1-i}\Bigg)\end{aligned} \]前面的东西 \(O(n)\) 乱做。咱考虑后面的东西。咱最好让 \(x\) 的指数正常一点,比如说我们这里内层循环枚举 \(k+1-i\):
\[\sum\limits_{k=0}^{n} \frac{a_k}{k+1}\sum\limits_{i=1}^{k+1}\binom{k+1}{k+1-i}B_{k+1-i}x^{i} \]然后组合数有对称性,里面的下面还是 \(i\),于是:
\[\sum\limits_{k=0}^{n} \frac{a_k}{k+1}\sum\limits_{i=1}^{k+1}\binom{k+1}{i}B_{k+1-i}x^{i} \]更换枚举顺序。
\[\sum\limits_{i=1}^{n+1}x^{i}\sum\limits_{k=i-1}^{n} \frac{a_k}{k+1}\binom{k+1}{i}B_{k+1-i} \]然后看看这整出来的一大坨系数咋算。拆开组合数。
\[\sum\limits_{i=1}^{n+1}x^{i}\sum\limits_{k=i-1}^{n} \frac{a_k}{k+1}\cdot \frac{(k+1)!}{i!(k+1-i)!}B_{k+1-i} \]一堆 \(k+1\),干脆枚举 \(k+1\)。
\[\sum\limits_{i=1}^{n+1}x^{i}\sum\limits_{k=i}^{n+1} \frac{a_{k-1}}{k}\cdot \frac{k!}{i!(k-i)!}B_{k-i} \]而且现在 \(i\) 和 \(k\) 的上界也一样了。舒服。分母的 \(k\) 和分子的 \(k!\) 约掉一个 \(k\):
\[\sum\limits_{i=1}^{n+1}\frac{x^i}{i!}\sum\limits_{k=i}^{n+1} \Bigg(a_{k-1}\cdot(k-1)!\Bigg) \frac{B_{k-i}}{(k-i)!} \]记 \(f_x=a_{x-1}\cdot (x-1)!,g_x=\dfrac{B_x}{x!}\)
原式变为:
\[\sum\limits_{i=1}^{n+1}\frac{x^i}{i!}\sum\limits_{k=i}^{n+1} f_k g_{k-i} \]我们可以考虑枚举 \(k-i\):
\[\sum\limits_{i=1}^{n+1}\frac{x^i}{i!}\sum\limits_{k=0}^{n+1-i} f_{k+i} g_k \]拜 Qcfff 所赐的惊人注意力,考虑翻转 \(f\)。记 \(f'_{n+1-k}=f_{k}\),有:
\[\sum\limits_{i=1}^{n+1}\frac{x^i}{i!}\sum\limits_{k=0}^{n+1-i} f'_{n+1-i-k} g_k \]就~能~算~了~
UVA12633 Super Rooks on Chessboard
题干:给你一个 \(n\times m\) 的棋盘,上面有 \(p\) 个“半皇后”,即覆盖一行、一列和一条左上到右下的对角线,求有多少个格子没有被覆盖。
首先借助 \(\color{red}\mathfrak{zzafanti}\) 之力,我们将棋盘顺时针旋转 \(90^{\circ}\),这样子做可以把对角线变成横坐标与纵坐标之和相等的线,方便后面计算。
我们先计算出所有被覆盖格子的数量。编号从 \(0\) 开始。
记:
- \(X_i=\begin{cases}0 & \text{第 }i \text{ 行没有棋子}\\1&\text{第 }i \text{ 行有棋子}\end{cases}\)
- \(Y_i=\begin{cases}0 & \text{第 }i \text{ 列没有棋子}\\1&\text{第 }i \text{ 列有棋子}\end{cases}\)
我们记旋转后 \(n\) 表示行数,\(m\) 表示列数。容易计算:
- 横线的数量 \(t_x=\sum\limits_{i=0}^{n-1}X_i\)
- 竖线的数量 \(t_y=\sum\limits_{i=0}^{m-1}Y_i\)
于是我们可以算出第一类贡献:
\[res\leftarrow t_x\times m+t_y\times n-t_x\times t_y \]即所有横线上的格子,加上所有竖线上的格子,再减去交叉点格子。
接下来我们依次考虑横纵坐标和为 \(0\sim n+m-2\) 的对角线。
设当前对角线横纵坐标和为 \(z\)。
容易得出该斜线穿过了多少条横线和竖线。设其跨过的行坐标范围为 \(lx\sim rx\),列坐标 \(ly\sim ry\),于是有:
\[res\leftarrow res + (rx-lx+1) - \sum\limits_{i=lx}^{rx}X_i-\sum\limits_{i=ly}^{ry}Y_i \]上式表达了先让这条斜线覆盖上其占有的格子,然后减去重复计算的横竖线。
这个贡献显然可以通过计算前缀和来计算。\(lx,rx,ly,ry\) 自己画个图找找规律就行了。
但这还不够!我们这条斜线每穿过一个横竖线交叉点时,其贡献就会被减掉两次!
于是我们考虑哪些点会被计算。我们发现,当两条横竖线横纵坐标之和为 \(z\) 时,它会被这条线穿过。
于是我们就多减了这么多:
\[res\leftarrow res + \sum\limits_{i=0}^{z}X_iY_{z-i} \]这是什么?卷积!而且长得很友好!
于是我们直接卷就行了!至此,我们成功把所有被染色的格子数量算了出来,别忘了我们索求的是未被染色的格子。于是:
\[res\leftarrow n\times m-res \]就是最终答案了!
P5667 拉格朗日插值2
疯狂抄题解。我抄抄抄抄抄抄抄抄抄抄
我感到罪恶感爬上了我的脊背。
题意:
给定一个不超过 \(n\) 次的多项式的 \(n+1\) 个点值 \(f(0),f(1) \dots f(n)\),和一个正整数 \(m\),求 \(f(m),f(m+1) \dots f(m+n)\)。
先回顾拉插:
给定 \(n+1\) 个点对 \((x_0,y_0)\dots(x_n,y_n)\),可以确定一个 \(n\) 次的多项式 \(f(x)\),满足 \(\forall i\in[0,n],f(x_i)=y_i\)。
求 \(f(m)\) 的值。
\[f(m)=\sum\limits_{i=0}^{n}y_i\prod_{j=0,j\neq i}^{n}\frac{m-x_j}{x_i-x_j} \]如果给定的点对为:
\[(0,y_0)\dots(n,y_n) \]就能写出进一步简化的式子:
\[f(m)=\sum\limits_{i=0}^{n}y_i\prod_{j=-,j\neq i}^{n}\frac{m-j}{i-j} \]根据题解,我们有:
\[f(m+x)=\sum\limits_{i=0}^{n}f(i)\prod_{j=0,j\neq i}^{n}\frac{m+x-j}{i-j} \]求积符号分别扔到分子分母,有:
\[f(m+x)=\sum\limits_{i=0}^{n}f(i)\frac{\prod\limits_{j=0,j\neq i}^{n}(m+x-j)}{\prod\limits_{j=0,j\neq i}^{n}(i-j)} \]易得分母为 \(i!\cdot (-1)^{n-i}\cdot (n-i)!\),分子为 \(\dfrac{(m+x)!}{(m+x-i)(m+x-n-1)!}\)(牢记此题中 \(n<m\))
于是有:
\[f(m+x)=\sum\limits_{i=0}^{n}\frac{f(i)}{i! (-1)^{n-i}(n-i)!}\cdot \dfrac{(m+x)!}{(m+x-i)(m+x-n-1)!} \]把中间的一项无关系数提出来:
\[f(m+x)=\frac{(m+x)!}{(m+x-n-1)!}\sum\limits_{i=0}^{n}\frac{f(i)}{i! (-1)^{n-i}(n-i)!}\cdot \dfrac{1}{m+x-i} \]发现里面就是卷积。
我们令:
\[u_i=\frac{f(i)}{i! (-1)^{n-i}(n-i)!} \]当 \(i>n\) 时 \(u_i=0\)。
还有一个:
\[v_i=\frac{1}{m-n+i} \]然后我们把 \(u\) 和 \(v\) 求个卷积,考察第 \(x\) 项系数:
\[(u*v)_x=\sum\limits_{i=0}^{x}\frac{f(i)}{i!(-1)^{n-i}(n-i)!}\cdot\frac{1}{m-n+x-i} \]再考察第 \(n+x\) 项系数:
\[(u*v)_{n+x}=\sum\limits_{i=0}^{n+x}\frac{f(i)}{i!(-1)^{n-i}(n-i)!}\cdot\frac{1}{m+x-i} \]由于 \(u_{\ge n}=0\),我们上界可以换成 \(n\),于是:
\[(u*v)_{n+x}=\sum\limits_{i=0}^{n}\frac{f(i)}{i!(-1)^{n-i}(n-i)!}\cdot\frac{1}{m+x-i} \]这说明了什么!
\[\begin{aligned}f(m+x)&=\frac{(m+x)!}{(m+x-n-1)!}\sum\limits_{i=0}^{n}\frac{f(i)}{i! (-1)^{n-i}(n-i)!}\cdot \dfrac{1}{m+x-i}\\&=\frac{(m+x)!}{(m+x-n-1)!}(u*v)_{n+x}\end{aligned} \]算就完了!
hdu 4656 Evaluation
给定 \(n,b,c,d\) 和数组 \(a_{0}\sim a_{n-1}\),我们有:
\[F(x)=\sum\limits_{i=0}^{n-1}a_ix^i \]令 \(x_k=b\times c^{2k}+d\),求 \(F(x_0)\sim F(x_{n-1})\)。
退市自拔。令 \(0\le m<n\)
\[F(b\times c^{2m}+d)=\sum\limits_{i=0}^{n-1}a_i(b\times c^{2m}+d)^i \]二项式定理拆开:
\[F(b\times c^{2m}+d)=\sum\limits_{i=0}^{n-1}\sum\limits_{j=0}^{i}a_i\dbinom{i}{j}b^jc^{2mj}d^{i-j} \]未知力量告诉我们:
没到这一步嘞呀!——\(\mathfrak{Q\color{red}{cfff}}\)
于是我们拆开组合数:
\[F(b\times c^{2m}+d)=\sum\limits_{i=0}^{n-1}\sum\limits_{j=0}^{i}a_i\dfrac{i!}{j!(i-j)!}b^jc^{2mj}d^{i-j} \]整理一下:
\[F(b\times c^{2m}+d)=\sum\limits_{i=0}^{n-1}a_ii!\sum\limits_{j=0}^{i}\dfrac{b^j}{j!}\cdot \frac{d^{i-j}}{(i-j)!}c^{2mj} \]然后孬坛的来了。咋处理 \(c^{2mj}\) 没有一点头猪。
\(\mathfrak{Q\color{red}{cfff}}\) 言:
更换枚举顺序。
谨遵指令之意:
\[F(b\times c^{2m}+d)=\sum\limits_{j=0}^{n-1}\dfrac{b^j}{j!}c^{2mj}\sum\limits_{i=j}^{n-1}a_ii!\cdot \frac{d^{i-j}}{(i-j)!} \]\(2mj=m^2+j^2-(m-j)^2\),于是:
\[c^{2mj}=\frac{c^{m^2+j^2}}{c^{(m-j)^2}} \]——\(\mathfrak{Q\color{red}{cfff}}\)
我们带进去:
\[F(b\times c^{2m}+d)=\sum\limits_{j=0}^{n-1}\dfrac{b^j}{j!}\cdot \frac{c^{m^2+j^2}}{c^{(m-j)^2}}\sum\limits_{i=j}^{n-1}a_ii!\cdot \frac{d^{i-j}}{(i-j)!} \]整理一下:
\[F(b\times c^{2m}+d)=c^{m^2}\sum\limits_{j=0}^{n-1}\dfrac{b^j}{j!}\cdot \frac{c^{j^2}}{c^{(m-j)^2}}\sum\limits_{i=j}^{n-1}a_ii!\cdot \frac{d^{i-j}}{(i-j)!} \]咱把 \(i\) 下界换一下,也就是枚举 \(i-j\)
\[F(b\times c^{2m}+d)=c^{m^2}\sum\limits_{j=0}^{n-1}\dfrac{b^j}{j!}\cdot \frac{c^{j^2}}{c^{(m-j)^2}}\sum\limits_{i=0}^{n-j-1}a_{i+j}(i+j)!\cdot \frac{d^i}{i!} \]把 \(a\) 翻转并乘一个阶乘系数,具体的,\(a'_{n-1-j}=a_{j}j!\),于是有:
\[F(b\times c^{2m}+d)=c^{m^2}\sum\limits_{j=0}^{n-1}\dfrac{b^j}{j!}\cdot \frac{c^{j^2}}{c^{(m-j)^2}}\sum\limits_{i=0}^{n-j-1}a'_{n-1-j-i}\cdot \frac{d^i}{i!} \]后面裸卷积,设 \(u_j=\sum\limits_{i=0}^{j}a'_{j-i}\cdot \dfrac{d^i}{i!}\),我们有:
\[F(b\times c^{2m}+d)=c^{m^2}\sum\limits_{j=0}^{n-1}\dfrac{b^j}{j!}\cdot \frac{c^{j^2}}{c^{(m-j)^2}}u_{n-j-1} \]有些脑瘫了。把 \(u\) 翻转过来,具体的,\(u'_j=u_{n-1-j}\),于是:
\[F(b\times c^{2m}+d)=c^{m^2}\sum\limits_{j=0}^{n-1}\dfrac{b^j}{j!}\cdot \frac{c^{j^2}u'_j}{c^{(m-j)^2}} \]一大坨。我们为了好看一点,记:
\[p_j=\frac{b^jc^{j^2}u_j'}{j!} \]于是有:
\[F(b\times c^{2m}+d)=c^{m^2}\sum\limits_{j=0}^{n-1}\frac{p_j}{c^{(m-j)^2}} \]后面是卷积很明显了,但上界很寄。我们不如分开算:
\[F(b\times c^{2m}+d)=c^{m^2}\Bigg(\sum\limits_{j=0}^{m}\frac{p_j}{c^{(m-j)^2}} + \sum\limits_{j=m+1}^{n-1}\frac{p_j}{c^{(m-j)^2}}\Bigg) \]第一部分就是裸卷积。设一下 \(q_m=\sum\limits_{j=0}^{m}\frac{p_j}{c^{(m-j)^2}}\),于是:
\[F(b\times c^{2m}+d)=c^{m^2}\Bigg(q_m + \sum\limits_{j=m+1}^{n-1}\frac{p_j}{c^{(m-j)^2}}\Bigg) \]后面是啥?我们知道:\((j-m)^2=(m-j)^2\),于是:
\[F(b\times c^{2m}+d)=c^{m^2}\Bigg(q_m + \sum\limits_{j=m+1}^{n-1}\frac{p_j}{c^{(j-m)^2}}\Bigg) \]考虑枚举 \(j-m-1\),有:
\[F(b\times c^{2m}+d)=c^{m^2}\Bigg(q_m + \sum\limits_{j=0}^{n-m-2}\frac{p_{j+m+1}}{c^{(j+1)^2}}\Bigg) \]烦人。令 \(p'_{n-1-j} = p_{j}\),有:
\[F(b\times c^{2m}+d)=c^{m^2}\Bigg(q_m + \sum\limits_{j=0}^{n-m-2}\frac{p'_{n-m-2-j}}{c^{(j+1)^2}}\Bigg) \]令 \(c'_j=\dfrac{1}{c^{(j+1)^2}}\),有:
\[F(b\times c^{2m}+d)=c^{m^2}\Bigg(q_m + \sum\limits_{j=0}^{n-m-2}p'_{n-m-2-j}c'_{j}\Bigg) \]终于!裸卷积!设 \(r_n=\sum\limits_{j=0}^{n}p'_{n-j}c'_{j}\),有:
\[F(b\times c^{2m}+d)=c^{m^2}(q_m + r_{n-m-2}) \]只需枚举。沙比提还要任意模数,出题人孬子全是泡。
BZOJ4836. 二元运算
给定一种运算:
\[a\operatorname{opt}b=\begin{cases}a+b & a<b\\a-b &a\ge b\end{cases} \]给定两个长度分别为 \(n,m\) 的数列 \(a,b\),然后 \(q\) 次询问,每次给定一个 \(c\),求有多少对 \((i,j)\) 满足 \(a_i\operatorname{opt}b_j=c\)。
首先看到分治标签,还发现值域和长度同级,于是我们考虑在值域上分治。
设 \(a\) 序列里数字 \(i\) 出现了 \(A_i\) 次,\(b\) 序列里数字 \(i\) 出现了 \(B_i\) 次。我们想要求出数组 \(c\),满足 \(c_i\) 为询问 \(i\) 的答案。
考虑当前分治的值域为 \([l,r]\)。
- 若 \(l=r\),则此时令 \(c_0\leftarrow c_0+A_l\times B_l\)。
考虑 \(\operatorname{opt}\) 的定义,显然当 \(a=b\) 时 \(a\operatorname{opt} b=a-b=0\),于是此时 \(a\) 和 \(b\) 都只能取 \(l\),他们之间做 \(\operatorname{opt}\) 运算只能得到 \(0\),于是把贡献加到 \(c_0\) 上。
- 若 \(l<r\),则考虑左半边和右半边合并时产生的贡献。
我们令 \(mid = \left\lfloor\dfrac{l+r}{2}\right\rfloor\),我们进行如下处理:
-
递归计算 \([l,mid]\),\([mid+1,r]\)。
-
考虑值域在 \([l,mid]\) 之间的 \(a\) 与值域在 \([mid+1,r]\) 之间的 \(b\) 相 \(\operatorname{opt}\) 的贡献。
这一部分贡献中因为 \(a<b\),有 \(a\operatorname{opt} b=a+b\),卷个积吧。
- 考虑值域在 \([l,mid]\) 之间的 \(b\) 与值域在 \([mid+1,r]\) 之间的 \(a\) 相 \(\operatorname{opt}\) 的贡献。
这一部分贡献中因为 \(a>b\),有 \(a\operatorname{opt} b=a-b\),把某一个数组翻转后,卷个积吧。
不难发现这个就是个整体二分的过程。照上面说的跑一遍就行了。
卷积的部分细节怪多的。
BZOJ3451. Tyvj1953 Normal
cy 锐评这种笔记意义不大。我不敢苟同。
题意:
time = 0
Solve(Tree a) {
time += a.size;
if (a.size == 1) return;
else {
select x in a;
delete a[x];
}
}
有这么一个点分治,按照上述伪代码运行,在选择 a 中的 x 节点并将其删除后,原树分成了好多个子树,然后对每个子树调用 Solve。
我们均匀随机地选择 x,求 time 的期望。
原本考虑了 \(f_i\) 表示 \(i\) 点被删掉时所处子树的大小,求:
\[E\left(\sum f_i\right)=\sum E(f_i) \]然后不会了。
发现其实把贡献拆开了,每个点的贡献可以这么计算:
设 \(f_i\) 表示 \(i\) 所处连通块中,\(i\) 在第几次被删掉。
答案其实还是 \(E\left(\sum f_i\right)\)。因为 \(i\) 所处连通块中,每删掉一个点,\(i\) 都为答案贡献了 \(1\)。
这个东西就能算了。等同于计算 \(\sum E(f_i)\),让我们分开考虑。
如果令 \(i\) 为根。每次删掉连通块中一个点,相当于把它和它的子树一并删掉。于是 \(E(f_i)\) 转化成了这个题:Game on Tree,答案为 \(\sum\limits_{j=1}^{n} \dfrac{1}{dep_j}\),其中 \(dep_i=1\)。
于是原题变成了:树上任选两个点,它们距离加一的倒数进行求和。我们称之为两个点的贡献之和。
这个可以点分治算。(用正确的点分治去算错误的点分治可还行)
对于当前根,我们需要统计跨过根的路径(包括路径一端在根上)。也就是统计两个点属于不同子树,它们的贡献之和。
可以容斥,也就是用整棵树中任意两个点的贡献之和,减去每颗子树中任意两个点的贡献之和。这两部分是规模不同的相同问题。
我们考虑其中任意一个。把这颗树(可能是原树或者某一棵子树)中的点的深度都拿出来,存一下,设一共有 \(n\) 个点,于是要求:
\[\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{n}\frac{1}{dep_i+dep_j+1} \]考虑 \(dep=i\) 的点共有 \(c_i\) 个,令 \(m=\max(dep_i)\),于是:
\[\sum\limits_{i=0}^{m}\sum\limits_{j=0}^{m}\frac{1}{i+j+1}c_ic_j \]枚举 \(k=i+j\):
\[\sum\limits_{k=0}^{2m}\frac{1}{k+1}\sum\limits_{i=0}^{k}c_ic_{k-i} \]就是卷积了,就能做了。
BZOJ3509. COUNTARI
给定一个长度为 \(n\) 的数组 \(a\),求有多少对三元组 \((i,j,k)\) 满足 \(a_k-a_j=a_j-a_i\)。
看到标签分块。于是我们分块。设块长为 \(T\)。
枚举一个块,复杂度 \(O(\dfrac{n}{T})\)。
分三部分计算。
-
对于 \(j\) 在块内,\(i,k\) 在块外的左右两侧,我们把块外两侧卷积起来,枚举 \(j\),\(O(1)\) 查找即可。复杂度 \(O(T+V\log V)\)
-
对于 \(i\) 和 \(j\) 在块内,\(k\) 在块外,我们枚举 \(i,j\),然后 \(O(1)\) 查找就行。复杂度 \(O(T^2)\)。\(j\) 和 \(k\) 在块内,\(i\) 在块外同理。
-
对于 \(i,j,k\) 都在块内,枚举 \(j,k\),然后在 \(j\) 的左边查找就行了。复杂度 \(O(T^2)\)。
总复杂度:\(O\left(\dfrac{n}{T}\cdot(T+V\log V)+T^2\right)=O(n+\dfrac{n}{T}V\log V+nT)\)。
玄学调调块长就行。
CF960G Bandit Blues
拜 Qcfff 与 _ANIG_ 所赐。
参见 九阳哥的博客。
设 \(f_{i,a}\) 表示一共 \(i\) 个互不相同的数,有 \(a\) 个前缀最大值的方案数。
神奇的枚举其中最小值的位置。最小值在第 \(1\) 个位置时,贡献为 \(f_{i-1,a-1}\),即作为前缀最大值。
不在第一个位置时,贡献为 \((i-1)f_{i-1,a}\),即为选择 \(i-1\) 中一个位置并不作为前缀最大值。
于是有:
\[f_{i,a}=f_{i-1,a-1} + (i-1)f_{i-1,a} \]就是第一类斯特林数。
\[f_{i,a} = \begin{bmatrix}i\\a\end{bmatrix} \]考虑答案的计算,枚举 \(n\) 的位置,有:
\[\sum\limits_{i=1}^{n}\binom{n-1}{i-1}f_{i-1,a-1}\times f_{n-i,b-1} \]也就是:
\[\sum\limits_{i=1}^{n}\binom{n-1}{i-1}\begin{bmatrix}i-1\\a-1\end{bmatrix}\times\begin{bmatrix}n-i\\b-1\end{bmatrix} \]算两行第一类斯特林数就行了。
P2791 幼儿园篮球题
但凡我能知道,斯特林数的性质……
多测,并给定一个 \(L\) 适用于每组测试;每次给定 \(n,m,k\),题意就是在求:
\[\frac{\sum\limits_{x=0}^{k}\dbinom{m}{x}\dbinom{n-m}{k-x}x^L}{\dbinom{n}{k}} \]分母乱做。分母。不会。瞟了一眼题解。第二类斯特林数???
第二类斯特林数有性质:
\[m^n=\sum\limits_{i=0}^{m}\begin{Bmatrix}n\\i\end{Bmatrix}i!\dbinom{m}{i} \]套进去!!!
\[\sum\limits_{x=0}^{k}\dbinom{m}{x}\dbinom{n-m}{k-x}\sum\limits_{i=0}^{x}\begin{Bmatrix}L\\i\end{Bmatrix}i!\dbinom{x}{i} \]组合数有性质:
\[\binom{n}{m}\binom{m}{k}=\binom{n}{k}\binom{n-k}{m-k} \]发现有两个组合数就是这式子左边。带进去!
\[\sum\limits_{x=0}^{k}\sum\limits_{i=0}^{x}\dbinom{m}{i}\dbinom{m-i}{x-i}\dbinom{n-m}{k-x}\begin{Bmatrix}L\\i\end{Bmatrix}i! \]之后就是套路推式子了。把 \(i\) 扔出去!
\[\sum\limits_{i=0}^{k}\begin{Bmatrix}L\\i\end{Bmatrix}i!\binom{m}{i}\sum\limits_{x=i}^{k}\dbinom{m-i}{x-i}\dbinom{n-m}{k-x} \]有一个神奇的东西,范德蒙德卷积的推论:
\[\sum\limits_{i=-l}^{r}\binom{n}{l+i}\binom{m}{r-i}=\binom{n+m}{l+r} \]发现原式子中 \(l=-i,r=k\),直接把式子带进去!
\[\sum\limits_{i=0}^{k}\begin{Bmatrix}L\\i\end{Bmatrix}i!\binom{m}{i}\binom{n-i}{k-i} \]我们知道第二类斯特林数 \(\begin{Bmatrix}L\\i\end{Bmatrix}\) 在 \(i>L\) 时取值为 \(0\),于是枚举上界改掉!
\[\sum\limits_{i=0}^{\min(k,L)}\begin{Bmatrix}L\\i\end{Bmatrix}i!\binom{m}{i}\binom{n-i}{k-i} \]于是预处理出一行第二类斯特林数,\(O(L)\) 回答询问即可。
BZOJ3684. 大朋友和多叉树
设 \(f_n\) 为根节点权值为 \(n\) 的方案数。其OGF为 \(F(x)\)。
我们有:
\[f_n=\sum\limits_{k\in D}[x^n]F(x)^k \]表达的含义就是:枚举根节点子树数量为 \(k\),然后 OGF 组合意义顺序拼接就有这玩意。
于是我们有:
\[F(x)=x+\sum\limits_{k\in D}F(x)^k \]这里加 \(x\) 的原因是:由于数据范围中 \(k\ge 2\),则 \(F(x)^k\) 中没有一次项;而 \(f_0=0,f_1=1\),一次项系数理应为 \(1\),故加上 \(x\)。
于是:
\[F(x)-\sum\limits_{k\in D}F(x)^k=x \]我们设 \(G(x)=x-\sum\limits_{k\in D}x^k\),有:
\[G\Big(F(x)\Big)=x\Leftrightarrow F\Big(G(x)\Big)=x \]我们知道 \(G(x)\),于是拉格朗日反演求出其复合逆 \(F(x)\) 的第 \(n\) 项值就行了!
CF914G Sum the Fibonacci
记 \(p_i=\sum\limits_{j=0}^{n}[s_j=i]\)。
我们求出:
\[A_k=\sum\limits_{i|j=k,i\&j=0}p_ip_j \]\[B_k=p_k \]\[C_k=\sum\limits_{i\otimes j=k}p_ip_j \]然后求出:
\[T_p=\sum\limits_{i\&j\&k=p}A_if(i)B_jf(j)C_kf(k) \]计算答案:
\[ans=\sum\limits_{k=0}^{17}T_{2^k} \]即可。
CF755G PolandBall and Many Other Balls
这下脑瘫了。
赛时做法:我们有:
\[ans_m=\sum\limits_{i=0}^{m}\binom{n-i}{i}\binom{n-2i}{m-i} \]一共选 \(m\) 组,其中枚举 \(i\) 组为两个,方案数通过插板法是 \(\dbinom{n-i}{i}\),剩余的 \(m-i\) 组都是一个,选法为 \(\dbinom{n-2i}{m-i}\),乘一下就有上式。
然后这个东西卷不了一点。卷个积吧。
正解:记 \(f(i,j)\) 为前 \(i\) 个数,放了 \(j\) 组的方案数。
我们有:
\[f(i,j)=f(i-1,j-1)+f(i-2,j-1)+f(i-1,j) \]分别为在 \(i\) 个位置放一个长度为 \(1\) 的,或者一个长度为 \(2\) 的,或者啥也不放。
初始值:\(f(0,0)=f(1,0)=f(1,1)=1\)。
记生成函数:
\[F_i(x)=\sum\limits_{j=0}f(i,j)x^j \]我们有递推式:
\[F_i(x)=(x+1)F_{i-1}(x)+xF_{i-2}(x) \]我们要求的就是 \([x^k]F_n(x)\),即 \(f(n,k)\)。初始值:\(F_0(x)=1,F_1(x)=x+1\).
我们写成转移矩阵:
\[\begin{bmatrix}F_{i-1}(x),F_{i-2}(x)\end{bmatrix}\times \begin{bmatrix}(x+1) &1\\x&0\end{bmatrix}=\begin{bmatrix}F_{i}(x),F_{i-1}(x)\end{bmatrix} \]这个容易证明。于是:
\[\begin{bmatrix}F_{1}(x),F_{0}(x)\end{bmatrix}\times \begin{bmatrix}(x+1) &1\\x&0\end{bmatrix}^{n-1}=\begin{bmatrix}F_{n}(x),F_{n-1}(x)\end{bmatrix} \]中间的东西矩阵快速幂套多项式乘法计算即可。时间复杂度 \(O(k\log k\log n)\)
CF1613F Tree Coloring
把一颗 \(n\) 个节点的树染成 \(n\) 种不同的颜色,使得每个节点都不是其父节点的颜色减一。
那个容斥我想了很久 ——jmc
于是我们考虑容斥。
我们要求的答案就是:任意染色的方案数,减去至少一对父子节点不合法的方案数,加上至少两对父子节点不合法的方案数……
由于颜色互不相同,对于某个节点,它最多有一个儿子的颜色是其减一。
记 \(c_i\) 为节点的儿子个数(不考虑叶子结点)。
考虑一共有 \(j\) 对父子节点不合法,这些父节点肯定互不相同。而对于某个父节点 \(i\),它可以选择 \(c_i\) 中任意一个,将其颜色染成 \(i\) 的颜色减一。
于是乎我们就转化成:求在 \(c_1\sim c_n\) 中任选 \(j\) 个,求其乘积,再把所有的乘积求和。算出这个后,我们把每对不合法的父子节点当成一组,分配颜色的方案就是 \((n-j)!\)。我们考虑解决前面的问题。
设 \(f(i,j)\) 为在前 \(i\) 个节点中选择 \(j\) 个,它们的 \(c\) 求积再求和的结果。我们转移:
\[f(i,j)=c_if(i-1,j-1) + f(i-1,j) \]很清晰。我们构造生成函数:\(F_i(x)=\sum\limits_{j=0}f(i,j)x^j\),于是有:
\[F_i(x)=(1+c_ix)F_{i-1}(x) \]初始值:\(F_0(x)=1\)。我们最终要求的就是 \(F_n(x)\) 的各项系数,于是我们求:
\[\prod\limits_{i=1}^{n}(1+c_ix) \]即可。这个东西分治 FFT 就能做,时间复杂度为 \(T(n)=2T(\dfrac{n}{2})+O(n\log n)=O(n\log^2n)\)。
于是答案就是:
\[\sum\limits_{i=0}(-1)^i\Big([x^i]F_n(x)\Big)(n-i)! \]CF1580F Problems for Codeforces
不会。抄题解。
其实题解里说的很详细了。这里写几个我认为不易理解的地方。
- 关于 \(T(x)=\dfrac{1}{1-A(x)}\)
其实是 \(T(x)=\sum\limits_{i=0}A(x)^i\),即枚举奇段个数,利用 OGF 组合意义顺序拼接得出。
为什么加上 \(A(x)^0\)?\(0\) 个奇段啥意思?其实加在了常数项上,我们又不用,所以加上去也没必要。
- 关于牛逼转化
对于相邻两个 \(S\) 和 \(B\),有:
\[\begin{aligned}&S+B<m\\ \Leftrightarrow &S+B-\left\lceil\frac{m}{2}\right\rceil < m-\left\lceil\frac{m}{2}\right\rceil\\ \Leftrightarrow &S+B'< \left\lfloor\frac{m}{2}\right\rfloor \end{aligned}\]所以能够和「\(m/2\) 序列」一一对应。
- 关于 \(a_{m,i}=f_{m/2,i}\)
这里只有当 \(i\) 为奇数且不为 \(1\) 时满足。其余情况:
-
\(a_{m,i}=0\),\(i\) 为偶数(毕竟是奇段,长度不能是偶数)
-
\(a_{m,1}=\left\lceil\dfrac{m+1}{2}\right\rceil\),只有一个数且必须是小数,根据小数的定义就有这个。
- 关于 \(F(x)=A(x)+\dfrac{B(x)^2}{1-A(x)}\)
先说后面 偶段 + 若干奇段 + 反的偶段 部分为什么是这个。
OGF 组合意义秒了。其实就是:
\[B(x)\times\Bigg(\sum\limits_{i=0}A(x)^i\Bigg)\times B(x) \]就是顺序拼接!中间的弄成封闭形式即可。
再说前面的 \(A(x)\)。为什么一段 \(\tt{BSBSB\dots BSB}\) 可以和一个奇段对应?对于每个数,我们都用 \(m-1\) 去减它,就能把所有的 \(\tt B\) 变成 \(\tt S\),把 \(\tt S\) 变成 \(\tt B\)。
CF662C Binary Table
我们设 \(a_i\) 为第 \(i\) 列从上往下当成一个二进制数,这个数是啥。
我们考虑枚举哪些行被反转。具体地,我们枚举一个 \(n\) 位的二进制数 \(i\),其中第 \(j\) 位为 \(1\) 表达第 \(j\) 行被反转(这里从 \(1\) 编号)。
我们发现 \(i\otimes a_j\) 就是第 \(j\) 列按照上述规则反转后的第 \(j\) 列组成的数。
对于一个 \(n\) 位的二进制数 \(x\),我们定义其 \(val\) 为:
\[val(x)=\min (i,x-i) \]其中 \(i\) 为 \(x\) 中 \(1\) 的出现次数。于是我们求的答案:
\[\min\limits_{i=0}^{2^{n+1}-1}\Bigg(\sum\limits_{j=1}^{m}val(i\otimes a_j)\Bigg) \]易于理解。紧接着,我们令:
\[b_i=\sum\limits_{j=1}^{m} [a_j=i] \]于是答案变为:
\[\min\limits_{i=0}^{2^{n+1}-1}\Bigg(\sum\limits_{j=0}^{2^{n+1}-1}b_j\cdot val(i\otimes j)\Bigg) \]我们如果求出:
\[C_i=\sum\limits_{i\otimes j=k}b_j\cdot val(k) \]答案就是 \(\min C_i\)。
我们有 \(j\otimes k=i\),于是:
\[C_i=\sum\limits_{j\otimes k=i}b_j\cdot val(k) \]做完了???
CF901E Cyclic Cipher
啊?
cy 评价别写了。过于抽象。
P4491 [HAOI2018] 染色
考虑容斥。我们记 \(op_i\) 为至少有 \(i\) 种颜色恰好出现 \(k\) 次的方案数。天才泉此方推出了下面的式子:
\[op_i=\dbinom{m}{i}\dbinom{n}{iS}\Bigg(\prod\limits_{j=0}^{i-1}\dbinom{iS-jS}{S}\Bigg)(m-i)^{n-iS} \]先从 \(m\) 个颜色中选 \(i\) 个,再从 \(n\) 个位置中选 \(iS\) 个位置来放这些颜色,中间的连乘是计算这些钦定的颜色内部的分配(理解为先放第一种颜色有 \(\dbinom{iS}{S}\) 种方案,再放第二种有 \(\dbinom{iS-S}{S}\) 种方案……乘起来),最后再乘上剩余位置瞎放的方案(只能放除去这 \(i\) 种颜色之外的颜色)。
看起来可没问题,我们容斥一下?
\[ans_{假}=\sum\limits_{i=0}^{\min(\lfloor\frac{n}{S}\rfloor,m)}w_i\times\sum\limits_{j=i}^{m}(-1)^{j-i}op_j \]但是错了,为什么呢?
比如说 \(11223\),我们钦定一种颜色出现两次时,钦定 \(1\) 和钦定 \(2\) 都会计数这种方案。
凭借直觉,我们发现这个额外重复计数的次数应该是个组合数。于是我们瞎乘个组合数:
\[ans_{真}=\sum\limits_{i=0}^{\min(\lfloor\frac{n}{S}\rfloor,m)}w_i\times\sum\limits_{j=i}^{lim}(-1)^{j-i}\dbinom{j}{j-i}op_j \]他就对了!
行。这个好像是二项式反演推出来的,但我们蒙对了!
剩余的就简单了。计算 \(op\) 可以 \(O(n)\) 预处理,\(10^7\) 显然能跑。
推一推容斥的式子,枚举 \(j-i\)(我们记 \(lim=\min(\left\lfloor\dfrac{n}{S}\right\rfloor,m)\)):
\[\sum\limits_{j=0}^{lim-i}(-1)^{j}\dbinom{j+i}{j}op_{j+i} \]组合数拆开:
\[\sum\limits_{j=0}^{lim-i}(-1)^{j}\frac{(j+i)!}{j!\cdot i!}op_{j+i} \]整理:
\[\frac{1}{i!}\sum\limits_{j=0}^{lim-i}\frac{(-1)^{j}}{j!}(j+i)!op_{j+i} \]减法卷积,反转数组!设 \(f_i=\dfrac{(-1)^i}{i!}\),\(g_i=i!\cdot op_i\),\(g'_{lim-i} = g_i\),原式变成:
\[\frac{1}{i!}\sum\limits_{j=0}^{lim-i}f_ig'_{lim-i-j} \]标准的卷积,ntt 就行!
P5110 块速递推
生成函数 \(F(x)=\sum\limits_{i=0}a_ix^i\),我们有:
\[F(x)=233xF(x)+666x^2F(x)+x \]也就是
\[F(x)=\frac{x}{1-233x-666x^2} \]解出来通项公式:
\[a_i=\frac{\left(\dfrac{233}{2}+\dfrac{13\sqrt{337}}{2}\right)^{n\bmod (p-1)}-\left(\dfrac{233}{2}-\dfrac{13\sqrt{337}}{2}\right)^{n\bmod (p-1)}}{2\left(\dfrac{13\sqrt{337}}{2}+\dfrac{233}{2} \right)-233} \]光速幂计算即可。
P5850 calc加强版
逆天抽象题。贺 Qcfff 的。
题干中的 \(k\) 这里替换成 \(K\)。
每种颜色的生成函数 \(F_k(x)=1+kx\),其中 \(k\in[1,K]\)。
答案的第 \(n\) 项就是 \(n!\times [x^n]\prod\limits_{k=1}^{K}F_k(x)\)。
求后面这个多项式相当于求:
\[\exp \sum\limits_{k=1}^{K}\ln F_k(x) \]我们有 \(\ln F(x)=\displaystyle \int \frac{F'(x)}{F(x)}\),于是:
\[\exp \sum\limits_{k=1}^{K}\int\frac{(1+kx)'}{1+kx} \]分子求导为 \(k\),于是:
\[\exp \sum\limits_{k=1}^{K}\int k\cdot (1+kx)^{-1} \]看这个逆怎么求。找规律发现 \((1+kx)^{-1}=\sum\limits_{i=0}(-kx)^i\),于是:
\[\exp \sum\limits_{k=1}^{K}\int k\sum\limits_{i=0}(-kx)^i \]把多项式积分的定义带进去:
\[\exp \sum\limits_{k=1}^{K}k\sum\limits_{i\ge 1}\frac{(-k)^{i-1}}{i}x^i \]更换枚举顺序:
\[\exp \sum\limits_{i=1}^{n}\frac{(-1)^{i-1}x^i}{i}\sum\limits_{k=1}^{K}k^i \]发现后面的是自然数幂和。但多次询问指数不会。故翻 OI-ing,找到了 \({\color{black}\mathfrak{z}}\color{red}\mathfrak{zafanti}\) 写的一文 《几个自然数幂和计算方法》 一文。里面介绍了一种 \(O(n\log n)\) 求出 \(i\in[1,n]\) 时 \(\sum\limits_{k=1}^{K}k^i\) 的每种取值方法:
我们构造 EGF:
\[\sum\limits_{i=0}\frac{\sum\limits_{k=1}^{K}k^i}{i!}x^i \]更换枚举顺序:
\[\sum\limits_{k=1}^{K}\sum\limits_{i=0}\frac{(kx)^i}{i!} \]发现后面的东西就是 \(e^{kx}\),于是:
\[\sum\limits_{k=1}^{K}e^{kx} \]等比数列求和公式:
\[\frac{e^{(n+1)x}-e^x}{e^x-1} \]这东西上下常数项都是 \(0\),于是同时除以 \(x\) 后多项式求逆就行了!
别忘了乘阶乘!
于是我们处理出 \(i\in[1,n]\) 时的自然数幂和,然后多项式 \(\exp\),就做完了。
普通版中 \(n\le 500\),于是我们直接暴力卷积,反正能跑就完了!
\[\begin{aligned}\\\\\\\\\\\\\\\\\\\\\end{aligned} \] 标签:frac,limits,cdot,多项式,sum,卷积,习题,binom From: https://www.cnblogs.com/baoyangawa/p/18091105