RMQ求Lca
怕考场被卡,所以临省选重新复习一下。
有个性质:若 \(u,v\) 不成祖先和儿子关系,则 \(u, v\) 的 \(lca\) 的 \(dfs\) 序一定不在 \(dfn_u\) 到 \(dfn_v\) 之间,所以我们只用找到 \(dfn_u\) 到 \(dfn_v\) 之间深度最小点 \(d\) 的就行了,\(d\) 的父亲显然是 \(u,v\) 的 \(lca\)。
manacher
思想是对于一个大的回文串,里面的小回文串在对应的另外一边也一定存在相同的小回文串。
每次要注意对于 \(maxR - i + 1\) 取 \(min\),
PAM
之前学了,但是当时就没学会,现在再学一遍还不太会。
值得注意的是:我们新建点必须在最后。
Tarjan
割点
tarjan果然还不会。
我们每次判断 \(dfn_{now}\) 是不是小于等于 \(low_{to_i}\),是表示 \(to_i\) 到不了 \(now\) 的祖先,所以这个点 \(now\) 就是割点。注意特判根的情况。
我们对于 \(dfn_{to_i} \neq 0\) 的情况,\(low\) 是与 \(dfn_{to_i}\) 取 \(min\),而不是与 \(low_{to_i}\) 取 \(min\)。原因看一下这篇大佬的文章的最后一部分。
缩点
果然还是没理解tarjan。
我们每次对于 \(low_{now}\) 和 \(low_{to_i}\) 取 \(min\) 的时候,只能与在栈里面的取 \(min\)。
不然可能会出现我们先处理的前面的点,在后面点处理的时候又对于前面的点取 \(min\),然后就错了。
还有每次弹栈的时候要把栈顶的 \(visit\) 变成 \(false\)
例如:
5 5
1 3 1 2 2
3 1
4 1
5 1
5 3
5 2
5
点双联通分量
我连定义都忘了。。。。记起来定义就行了。
定义是:一个联通块内没有割点。
边双联通分量
没有割边的连通块。
注意判断割边的条件是 \(low_v > dfn_{now}\)。
CDQ 分治
我怎么写一道板子发现不会一道。。
CDQ还是有很多要注意的。
比如在相等的可以算贡献时要去重,第一次排序要以 \(a,b,c\) 为关键字都排一遍,不能只按 \(a\) 排序。
因为我们要让左边的贡献给右边,所以我们要让能贡献的在前面,被贡献额在后面。
然后还有个要注意清空就没了。
SAM(重点不会)
都忘了,都忘了,哈哈,我直接趋势。
对于每次加点,把从 \(last\) 开始的所有空的点向上跳 \(link\) 并都连上 \(newP\)。
所以当我们之后建新点的时候若从 \(x\) 找到了 \(newP\),并将 \(newP\) 分裂成 \(q\) 和 \(newQ\),我们从 \(x\) 向跳 \(link\) 的过程中只会把 \(x\) 及以上的点连向 \(newQ\)。而 \(last\) 向上跳 \(link\) 一直到 \(x\) 连的边还是 \(q\)。
广义SAM
先建一个trie,然后依靠trie建SAM。
每次建SAM的新节点的时候,都将trie树上这一点的父亲 \(fa\) 在SAM中建出点的 \(newP\) 设为 \(last\) 就行了。
exgcd(重点不会)
破防了哥,我数学就是个jb。
首先我们要证 \(gcd(a, b) = gcd(b,a \mod\ b)\)。
我们设 \(r=a \mod b\),因为 \(a \mod b=a-\lfloor \frac{a}{b} \rfloor \cdot b\),设 \(k=\lfloor \frac{a}{b} \rfloor\),所以 \(r=a-k \cdot b\)。因为 \(\frac{a-k \cdot b}{gcd(a,b)}\) 一定是整数,所以 \(\frac{r}{gcd(a,b)}\) 也是整数。反之同理。
然后就可以 \(ax+by=bx+(a \% b) y\) 然后就能解决了。
因为我们求的时候是等同于 \(a\cdot x + b \cdot y = gcd(a, b)\) 求的。所以记得从 \(exgcd\) 出来后将 \(x,y\) 都乘上 \(\frac{c}{gcd(a,b)}\)。
关于通解的求法
我们首先可以知道 \(a(x+k \cdot b)+b(y-k \cdot a)=c\) 是等同与原式子 \(ax+by=c\)。我们设 \(dx = k\cdot b\) 和 \(dy = k \cdot a\)。我们只需要让 \(dx,dx\) 同时是整数就行。当 \(k=\frac{1}{gcd(a,b)}\) 时可以让 \(k \cdot b\) 和 \(k \cdot a\) 最小。
所以我们的通解(其中 \(s\) 为变量):
\[x=x+s \cdot dx \]\[y=y-s \cdot dy \]然后求就完事了。
主席树
没啥好说的,算比较简单的一个,只是要注意一下空间,可能不太好把控开多大。
线段树合并
这个有个特别要注意的点,就是我们如果将 \(b\) 合并到 \(a\) 上,那么合并之后会破坏 \(a\) 原本的结构,可能就会导致答案不一样。解决方法是每次合并的时候新建一个点,把 \(a\) 上面的值都赋给新建的点 \(New\),然后接下来合并的时候都合到新建的点 \(New\) 上面就行了。
还有个东西,每次 \(Merge\) 了叶子节点之后,要重新更新一遍叶子结点的各个权值。
点分治
还是很简单的,就是代码细节有点多。
注意要多判 \(visit_{to_i} = true\)。然后每次求重心的时候记得将 \(root=0\) 并且 \(sum=size_{to_i}\)。
平衡树 (重点看)
只写 \(FHQ\) 了,不写其他太麻烦的了。
唯一不太会的就是 \(Merge\) 和 \(Split\) 了
代码贴下面了。
Treap
void Split(int id, int value, int &l, int &r) {
if (id == 0) {
l = r = 0;
return;
}
if (val[id] <= value) {
l = id;
Split(child[id][1], value, child[id][1], r);
//这里面第二个child[id][1]取址了,会改变原id点的信息
//所以对应的id要pushup 下面同理
}
else {
r = id;
Split(child[id][0], value, l, child[id][0]);
}
Pushup(id);
return;
}
int Merge(int l, int r) {
if (!l || !r) {
return l | r;
}
if (key[l] <= key[r]) {
child[l][1] = Merge(child[l][1], r);
Pushup(l);
return l;
}
else {
child[r][0] = Merge(l, child[r][0]);
Pushup(r);
return r;
}
}
网络流(重点)
最大流
黑盒算法呜呜呜。
我们每次 \(Bfs\) 时把图分出来层,然后同时把 \(cur\) 数组赋值成 \(head\) 数组。
然后在 \(Dfs\) 的时候每次遍历边都重新更新一下 \(cur\) 以保证复杂度。我们的循环跳出条件既要保证 \(i \neq 0\) 还要保证 \(rest \neq 0\)。
还有个小优化就是每次判断流 \(temp\) 是不是等于 \(0\),若是的话就将 \(deep_{to_i}\) 赋值成 \(0\)。
注意千万不要打顺手了然后把 Dfs(to[i], end, std::min(rest, cap[i])) 打成 Dfs(to[i], now, std::min(rest, flow))!!!!!!
还有一定要在for循环加上 rest!=0
费用流
把 \(bfs\) 写成 \(spfa\)。
但是其中要改变好多细节。
我们要新加一个 \(visit\) 数组,表示我们有没有经过。在 \(spfa\) 中是判断在不在队列里, \(Dfs\) 中判断有没有在路径里,防止出现负环无限跑的情况。
然后每次要更新 \(cur\),还有判断 \(rest \neq 0\)。这些我老容易忘。
扩展域并查集
原本要写线段树分治的,但是发现自己不会“板子题”的前置知识,就只能来学了。
其实就是我们让两个点必须在不同的集合,然后就没了。例如:关押罪犯。
算了,我发现自己还是不会,重新在学一遍。(膜拜5k)。
我们判断一个图是不是二分图:
我们每次将两个点 \(u,v\) 连边的时候,将 \(u\) 与 \(v+n\) 连边,将 \(u+n\) 与 \(v\) 连边。表示 \(u\) 与 \(v\) 是敌人。
若我们 \(u,v\) 在同一个并查集里面,那么就说明 \(u\) 是 \(v\) 敌人的敌人,也就是朋友。
若我们此时再让 \(u\) 与 \(v+n\) 连边,那么 \(u,v\) 又是敌人又是朋友,就肯定不能成为二分图了。
数学上来解释,就是当从左半部分连向右半部分再连会左半部分时,连的边数一定是偶数,若我们再加一条边就成奇数了,肯定不是二分图了。
线段树分治
没时间写了,具体说一说思想吧。就是每次我们将输入的内容中,可以影响的区间放到线段树上。
然后每到一个节点,就将该节点的信息维护一下,直到叶子节点时输出答案。记得撤销维护。
李超线段树
好像思想还是比较好理解的,也比较好写。
我们加线段分成三种情况考虑:
-
新加的线段整个的比原来的高,那么直接覆盖就行。
-
新加的线段整个的比原来的低,那么直接退出不用管了。
-
新加的线段与原来的线段有交点,那么让 \(mid\) 处 \(y\) 大的做线段树上的线段,接着递归到剩下线段高的内一半去更新。
查询点就直接从根节点一直查询到叶子节点,每次把当前线段树节点代表的线段和之前查询的最优点,比较,更新一下就行了。
高斯消元(易错)
呃呃呃,果然我们高斯消元是有实力的。我一直被狂 \(hack\) 不止。
下面说一说易错点:
-
我们在找主元的时候,找的是绝对值最大的一行,所以要
std::fabs(a.matrix[i][j]) > std::fabs(a.matrix[result][j])。为了不找到 \(0\)。 -
我们在判断主元的值是不是 \(0\) 的时候,不能直接判断等不等于 \(0\),而是要判断绝对值是不是小于等于\(1e-10\)。注意是 绝对值。
-
我们在判断是不是无解的时候,判断的是 绝对值,注意是 绝对值 是不是大于等于 \(1e-9\)。
emmmmm,我最喜欢绝对值了。QAQ。
2-SAT
捏麻麻滴,tarjan狂错不止。
其实思想和扩展域并查集有点像。我们对于 \(a=0\) 或 \(b=0\) 的情况,我们如果 \(a \neq 0\), 那么 \(b\) 肯定等于 \(0\)。所以将 \(a \neq 0\) 的情况和 \(b=0\) 的情况建边就行了, \(b\) 的建边同理。
我们最后统计答案的时候,对于不可能的情况一定存在 \(a\) 与 \(a+n\) 在同一个联通块里,判断一下。还有输出是 \(true\) 还是 \(false\) 的时候,看谁的联通块的编号小就输出谁。因为编号小的一定是后走到的。
但是最后注意 \(tarjan\) 里弹栈时要清空弹出来元素的 \(visit\)。
哈哈,逆天 \(tarjan\)。
欧拉路径
重学一遍感觉受益匪浅。
转载自大佬的文章
欧拉路径定义:
图中经过所有边恰好一次的路径叫欧拉路径(也就是一笔画)。如果此路径的起点和终点相同,则称其为一条欧拉回路。
欧拉路径判定(是否存在):
-
有向图欧拉路径:图中恰好存在 \(1\) 个点出度比入度多 \(1\)(这个点即为 起点 \(S\)),\(1\) 个点入度比出度多 \(1\)(这个点即为 终点 \(T\)),其余节点出度=入度。
-
有向图欧拉回路:所有点的入度=出度(起点 \(S\) 和终点 \(T\) 可以为任意点)。
-
无向图欧拉路径:图中恰好存在 \(2\) 个点的度数是奇数,其余节点的度数为偶数,这两个度数为奇数的点即为欧拉路径的 起点 \(S\) 和 终点 \(T\)。
-
无向图欧拉回路:所有点的度数都是偶数(起点 \(S\) 和终点 \(T\) 可以为任意点)。
注:存在欧拉回路(即满足存在欧拉回路的条件),也一定存在欧拉路径。
当然,一副图有欧拉路径,还必须满足将它的有向边视为无向边后它是连通的(不考虑度为 \(0\) 的孤立点),连通性的判断我们可以使用并查集或 dfs 等。
我们用栈的原因是可以防止走错路径,而如果走错了路径,我们还能新加没走的路径。
具体情况如图: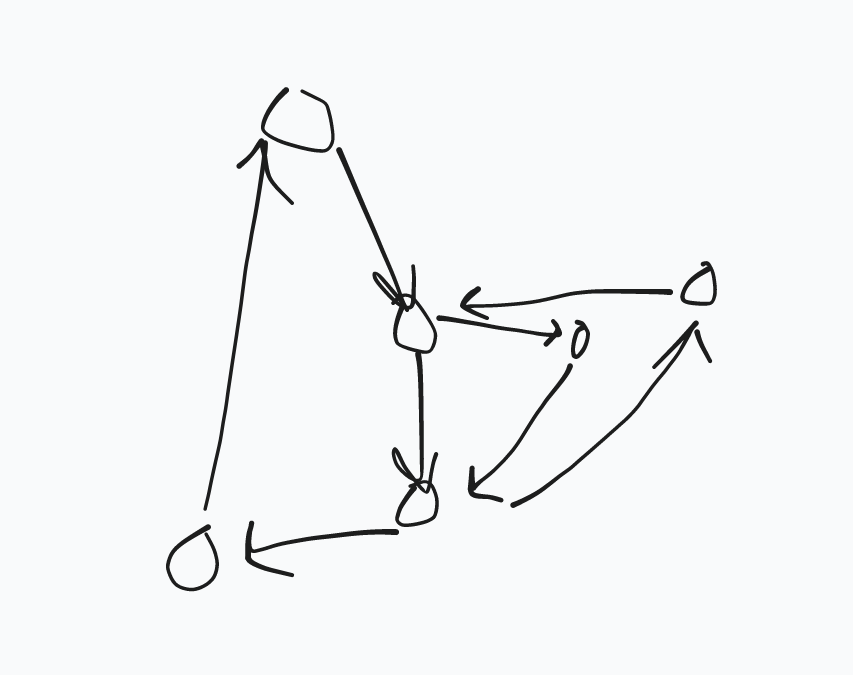
我们可能走成下图: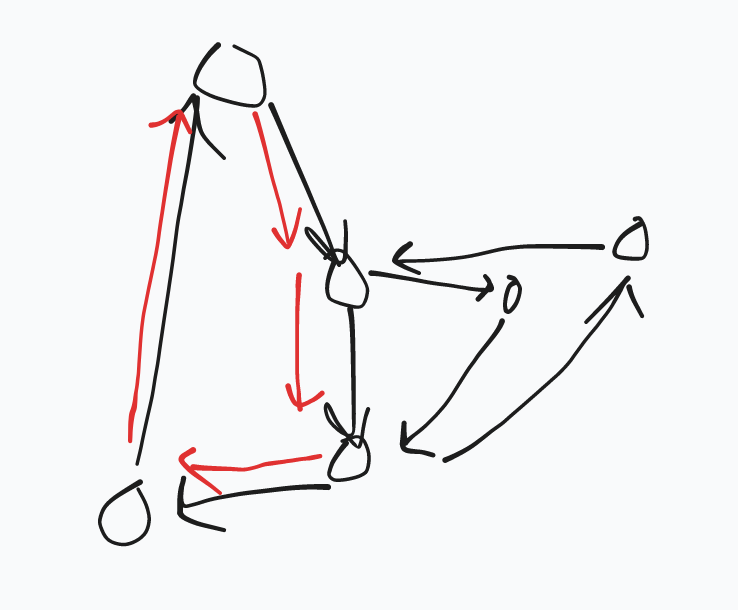
这个时候我们若 \(DFS\) 到哪里就输出哪里显然会错。
但是如果我们这个时候用栈存上了,我们就会把右半部分存到红色路径的上面,输出的时候会先输出,然后就对辣。
扫描线
忘了,又重新学了一遍。
里面其实是有很多细节的呀。
例如我们的线段树里面的每一个节点(即使是叶子节点也是)表示的是一段区间。
若我们线段树的区间是 \(l,r\) 那么我们表示的 \(x\) 的范围是 \(x_l,x_{r+1}\)。
这样是为了我们更新的时候可以断开区间,不然 \(mid\) 到 \(mid+1\) 的这一段区间取不到辣。
我们对于 pushup 也要改一下下。
我们每次给完全覆盖的区间的 \(sum\) 加 \(1\),然后在 \(pushup\) 的时候判断一下当前节点的 \(sum\) 是不是大于 \(0\)。
若是则当前区间的被覆盖的范围就是整个区间 \(len_{id}=x_{r+1}-x_{l}\),否则就是 \(lid\) 和 \(rid\) 覆盖的区间和 \(len_{id}=len_{lid}+len_{rid}\)。
要离散化一下, \(x\) 数组去重后若有 \(n\) 个,线段树的区间范围是 \(1,n-1\),我们遍历线段的时候也是到 \(2*N-1\)。
标签:记录,cdot,线段,路径,节点,模板,我们,欧拉 From: https://www.cnblogs.com/jueqingfeng/p/18035057