首页 > 其他分享 >浅谈计算几何

浅谈计算几何

时间：2024-02-28 22:16:32浏览次数：28  
标签：cnt return 浅谈 int double kMaxN vec 计算 几何

从目前局势来看，@0616allen要被处刑了呢

前置知识：

维度：

维度是一个非常抽象的东西。
在生活中常用的是 \(0\) 到 \(3\) 维，其对应如下：

\(0\) 维：点

\(1\) 维：线

\(2\) 维：面

\(3\) 维：体

每一维经过移动可以变成更高维，如点移动变成线，面移动变成体。

这不就不怕二向箔了吗

向量：

向量，顾名思义就是只有方向和大小的量。
向量没有位置属性，用 \(\vec{AB}\) 表示。

在做题中，常常可以用到向量没有位置的特性，比如在存储把向量时把一端移动到原点，这样就只需要存储另外一个点的位置即可。

向量的运算：

加法：

令 \(\vec{OA}=(x,y)\), \(\vec{OB}=(s,t)\)，则有：

\[\vec{OA}+\vec{OB}=\vec{OB}+\vec{OA}={}(x+s,y+t) \]

减法：

令 \(\vec{OA}=(x,y)\), \(\vec{OB}=(s,t)\)，则有：

\[\vec{OA}-\vec{OB}=(x-s,y-t) \]

点乘：

令 \(\vec{OA}=(x,y)\), \(\vec{OB}=(s,t)\)，则有：

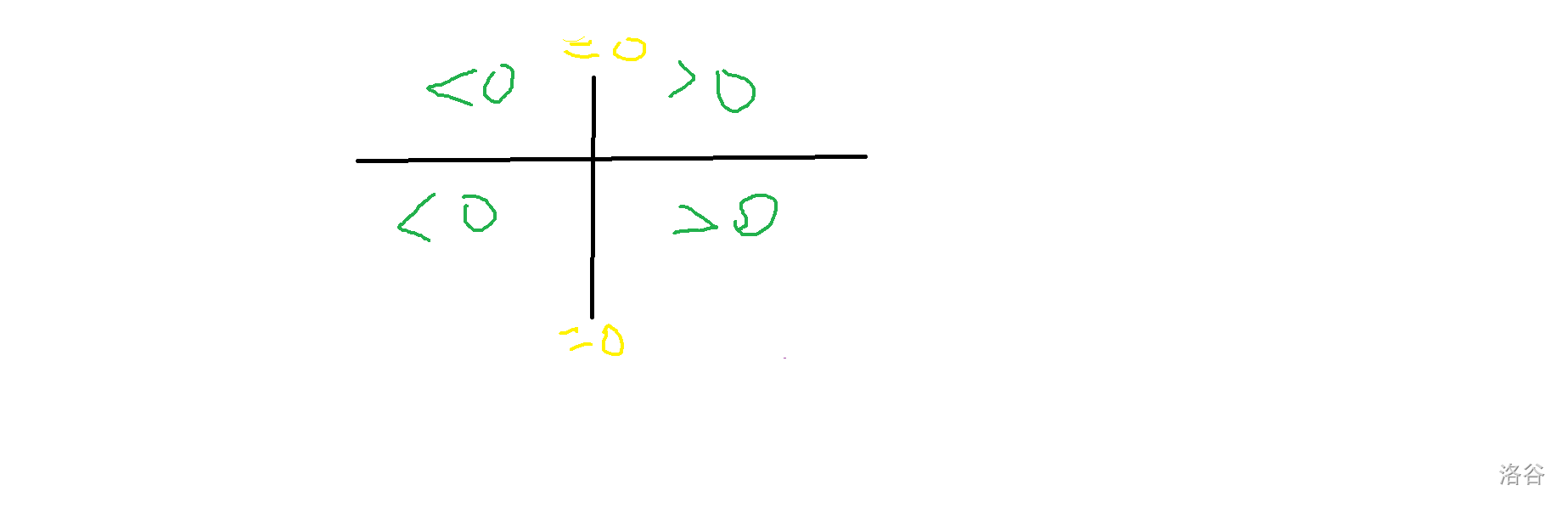
\[\vec{OA} \cdot \vec{OB}=\vec{OA} \cdot \vec{OB}=x\times s+y\times t \]

点乘可以判断向量在直角坐标系中的前后关系，与 \(y\) 轴正方向做点乘结果如图：

叉乘：

令 \(\vec{OA}=(x,y)\), \(\vec{OB}=(s,t)\)，则有：

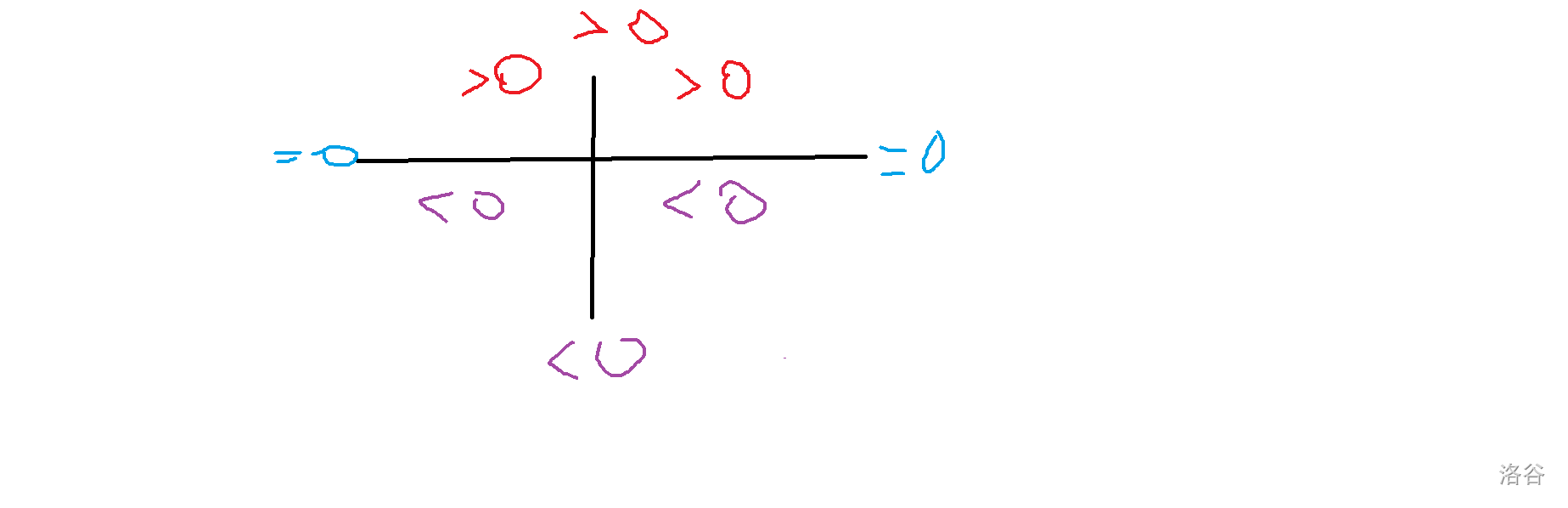
\[\vec{OA} \cdot \vec{OB}=x\times t+y\times s \]

叉乘在计算几何的运用较多，其可以判断向量在直角坐标系中的左右关系，与 \(x\) 轴正方向做叉乘结果如图：

叉乘的直接利用：

题目

首先显然可以把每个向量的极角算出来，然后直接排序。
但 9 种情况分讨显然不可取。
如果你想更深刻的体验计算几何的《快乐》当我没说。

不难想到，我们在排序时其实只需要两个向量的位置关系即可，所以可以直接用叉乘判断两个向量的位置关系即可。

由于在 360° 2 π 的极角范围内，向量不断左旋会造成循环，所以要把 \(y\) 为正和 \(y\) 为负分开排序。

code:

#include <algorithm>
#include <iostream>

using namespace std;
#define LL long long

const int kMaxN = 1e5 + 5;

struct X {
  LL x, y;
} a[kMaxN], l[kMaxN], r[kMaxN];

int vis[kMaxN], cnt[3], n, p, t;

LL D(X x) {
  return x.x * x.x + x.y * x.y;
}

bool C(X y, X x) {
  if (!y.x && !y.y) {
    return 0;
  }
  LL v = x.x * y.y - y.x * x.y;
  return v < 0 || !v && D(x) > D(y);
}

int main() {
  cin >> n;
  for (int i = 1; i <= n; i++) {
    cin >> a[i].x >> a[i].y;
    if (!a[i].x && !a[i].y) {
      cnt[2]++;
    } else if (a[i].y > 0 || a[i].x > 0 && !a[i].y) {
      l[++cnt[0]] = a[i];
    } else {
      r[++cnt[1]] = a[i];
    }
  }
  for (int i = 1; i <= cnt[2]; i++) {
    cout << "0 0\n";
  }
  sort(l + 1, l + cnt[0] + 1, C);
  sort(r + 1, r + cnt[1] + 1, C);
  for (int i = 1; i <= cnt[0]; i++) {
    cout << l[i].x << " " << l[i].y << "\n";
  }
  for (int i = 1; i <= cnt[1]; i++) {
    cout << r[i].x << " " << r[i].y << "\n";
  }
  return 0;
}

（不过感觉代码有点写丑了）。

正文

没错前面都是前置。

图形间的关系：

这里关系很多，且都很复杂，感觉以后有空或许要全部放个代码（？

点与直线的关系：

若点 \(O\) 在直线 \(PQ\) 上，则称 \(O\),\(P\),\(Q\) 三点共线。

三点共线时有：

\[\vec{OP}\times\vec{OQ}=0 \]

直线与直线的关系：

直线间的关系分为平行，相交和重合。

假设现在又两条直线 \(ST\) 和 \(AB\)。

首先，若 \(\vec{ST} \times \vec{AB}\neq 0\)，则两直线相交。

然后在一条直线上随便选取一点，若另一条直线也经过该点则两直线重合，否则平行。

点与线段的关系：

用斜率式算出线段中 \(y\) 坐标与那个点 \(y\) 坐标相同的点的 \(x\)，判断这个 \(x\) 与点的 \(x\) 是否相同即可。

然后当这条线段所在直线垂直于 \(x\) 轴时要特殊处理。

线段和线段的关系：

用斜率式解方程算出两个线段所在直线的交点，然后分别判断该点与两条线段的关系即可。

点与简单多边形的关系：

首先用点与线段的关系判掉在多边形边上的情况。

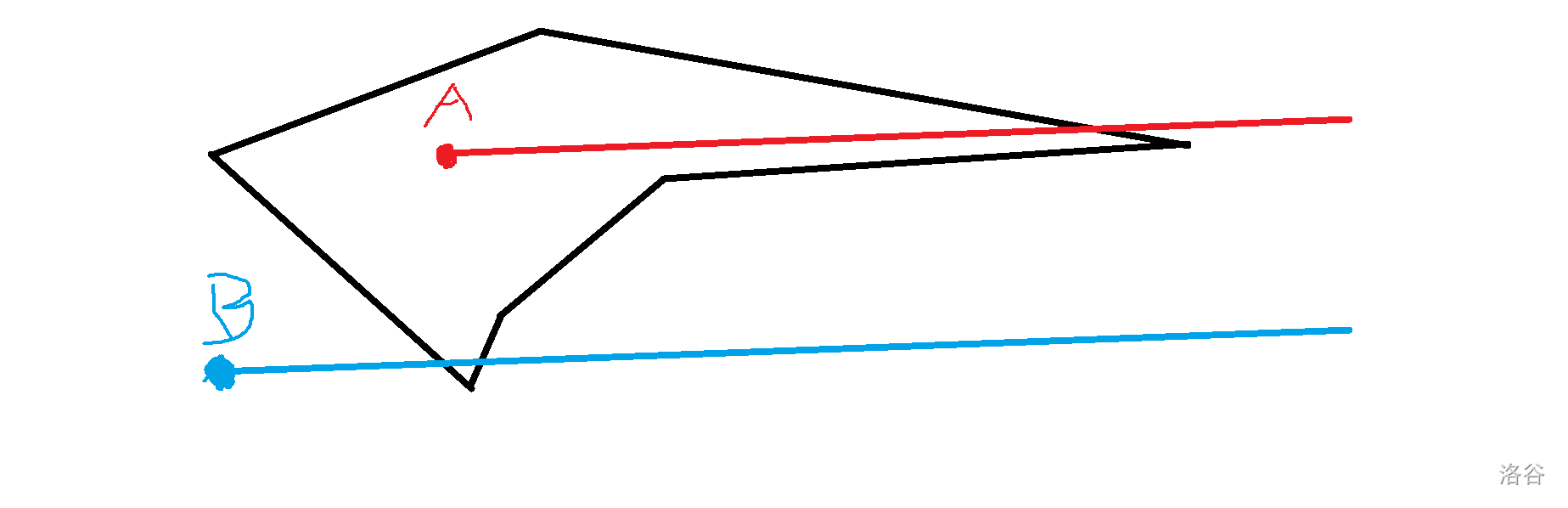
然后用射线法计算点向某一个方向无限延长所经过的边的奇偶性，奇数条边在内部，偶数条边在外部。

为了防止射线在计算边的时候遇到点而重复计算，可以偏移一定的度数。
当坐标最大值为 \(x\) 时，射线所在直线斜率最好为 \(\frac{1}{2x}\)。

如图：

多边形面积：

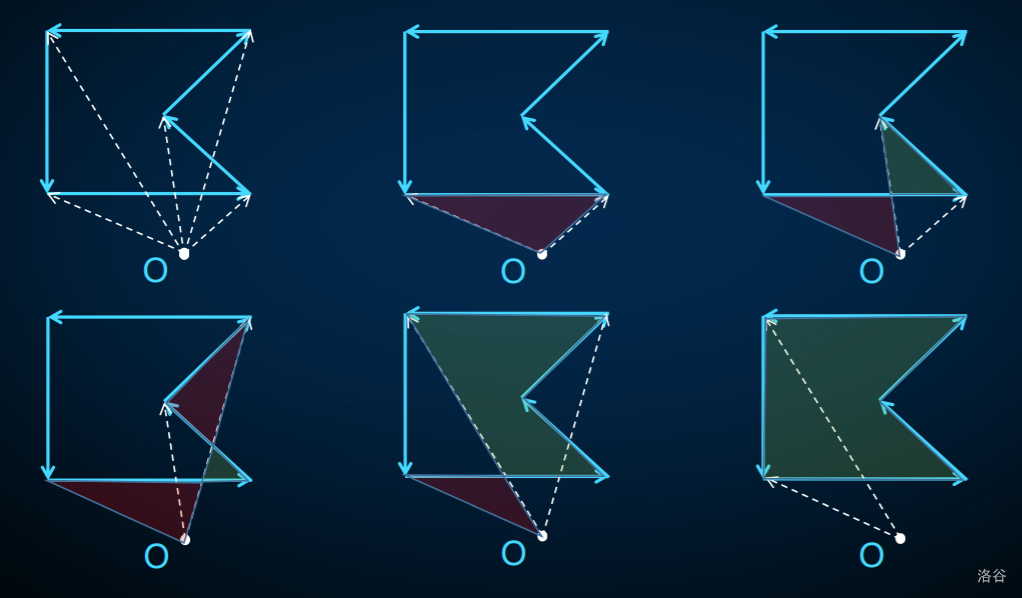
逆时针 枚举每一条边，然后计算负 \(y\) 轴与该边的叉积，将其累加就可以得到答案，如图：（自己画的图太抽象了，还是用 pty 的吧绝对不是因为懒）

建立凸包：

找到所有点中在直角坐标系上最靠左的点作为参照点（该点一定在凸包上），然后按照极角对所有点排序，依次加点即可。

但是这样去选取最后可能会变为一个凹边形，所以维护一个栈，然后每次用最后的线段与新线段做叉积，判断新线段是否更靠左。

code:


........

double M(int a, int b, int c) {
  return (x[b] - x[a]) * (y[c] - y[a]) - (x[c] - x[a]) * (y[b] - y[a]);
}

double D(int l, int r) {
  return sqrt((x[r] - x[l]) * (x[r] - x[l]) + (y[r] - y[l]) * (y[r] - y[l]));
}

bool C(int x, int y) {
  double v = M(0, x, y);
  return v > 0 || !v && D(x, 0) < D(y, 0);
}

........

for (int i = 1; i <= n; i++) {
  id[++cnt] = i;
  if (x[i] < x[0]) {
    x[0] = x[i], y[0] = y[i];
  } else if (x[i] == x[0]) {
    y[0] = min(y[0], y[i]);
  }
}
sort(id + 1, id + cnt + 1, C);
for (int i = 1; i <= cnt; i++) {
  for (; r > 1 && M(q[r - 1], q[r], id[i]) <= 0; r--) {
  }
  q[++r] = id[i];
}
for (int i = 1; i < r; i++) {
  lx += D(q[i], q[i + 1]);
}
lx += D(q[1], q[r]);

........

\(lx\) 为最后的答案。

题目选讲：

A

考虑到路线一定经过了洞旁边的点，所以对每对点之间建边（把起点和终点也放进去），然后枚举线段，判断是否存在严格交。
每条边的长度是两点的曼哈顿距离。
最后跑一边最短路即可。

code:

#include <cmath>
#include <iostream>
#include <queue>

using namespace std;
#define double long double

const int kMaxN = 505;
const double eps = 1e-7;

struct T {
  int id;
  double x;

  bool operator<(const T &a) const {
    return x > a.x;
  }
};

struct A {
  double s, a, b, c, d;
} q[kMaxN];

int n, cnt, vis[kMaxN];
double x[kMaxN], y[kMaxN], a[kMaxN][kMaxN], dis[kMaxN];

bool C(int idx, int idy) {
  if (x[idy] == x[idx]) {
    return 0;
  }
  for (int i = 1; i <= n; i++) {
    if (q[i].s >= x[idx] && q[i].s <= x[idy]) {
      double k = (y[idy] - y[idx]) / (x[idy] - x[idx]);
      double py = y[idx] + fabs(q[i].s - x[idx]) * k;
      if (!(py >= q[i].a && py <= q[i].b || py >= q[i].c && py <= q[i].d)) {
        return 0;
      }
    }
  }
  return 1;
}

int main() {
  while (cin >> n) {
    if (n == -1) {
      return 0;
    }
    x[++cnt] = 0, y[cnt] = 5;
    for (int i = 1; i <= n; i++) {
      double s, a, b, c, d;
      cin >> s >> a >> b >> c >> d;
      x[++cnt] = s, y[cnt] = a;
      x[++cnt] = s, y[cnt] = b;
      x[++cnt] = s, y[cnt] = c;
      x[++cnt] = s, y[cnt] = d;
      q[i].s = s, q[i].a = a, q[i].b = b, q[i].c = c, q[i].d = d;
    }
    x[++cnt] = 10, y[cnt] = 5;
    for (int i = 1; i <= cnt; i++) {
      for (int j = 1; j <= cnt; j++) {
        if (C(i, j)) {
          a[i][j] = sqrt((x[i] - x[j]) * (x[i] - x[j]) + (y[i] - y[j]) * (y[i] - y[j]));
        } else {
          a[i][j] = 1e9;
        }
      }
    }
    dis[1] = 0;
    fill(dis + 2, dis + cnt + 1, 1e9);
    priority_queue<T> q;
    T tt;
    tt.id = 1, tt.x = 0;
    for (q.push(tt); !q.empty();) {
      int x = q.top().id;
      q.pop();
      if (!vis[x]) {
        vis[x] = 1;
        for (int i = 1; i <= cnt; i++) {
          if (dis[i] > dis[x] + a[x][i]) {
            T st;
            st.id = i, st.x = dis[i] = dis[x] + a[x][i];
            q.push(st);
          }
        }
      }
    }
    printf("%.2Lf\n", dis[cnt]);
    fill(vis + 1, vis + cnt + 1, 0);
    cnt = 0;
  }
  return 0;
}

B

发现 \(n\) 很小，所以暴力枚举每个树砍不砍，然后对没有砍的那些树的点求一边凸包周长。
然后看砍下的长度是否大于等于凸包周长，合法就选择价值最小的即可。

code:（一定要注意输出格式啊！！！！洛谷输出格式是错的！！）

#include <algorithm>
#include <cmath>
#include <iostream>
#include <vector>

using namespace std;
#define LL long long;

const int kMaxN = 16;

double x[kMaxN], y[kMaxN], v[kMaxN], l[kMaxN], q[kMaxN], px, ans;
int vis[kMaxN], id[kMaxN], n;
vector<int> t;

double M(int a, int b, int c) {
  return (x[b] - x[a]) * (y[c] - y[a]) - (x[c] - x[a]) * (y[b] - y[a]);
}

double D(int l, int r) {
  return sqrt((x[r] - x[l]) * (x[r] - x[l]) + (y[r] - y[l]) * (y[r] - y[l]));
}

bool C(int x, int y) {
  double v = M(0, x, y);
  return v > 0 || !v && D(x, 0) < D(y, 0);
}

void D(int s, double sum, double len) {
  if (s > n) {
    int cnt = 0, r = 0;
    double lx = 0;
    x[0] = 1e9, y[0] = 1e9;
    for (int i = 1; i <= n; i++) {
      if (!vis[i]) {
        id[++cnt] = i;
        if (x[i] < x[0]) {
          x[0] = x[i], y[0] = y[i];
        } else if (x[i] == x[0]) {
          y[0] = min(y[0], y[i]);
        }
      }
    }
    sort(id + 1, id + cnt + 1, C);
    for (int i = 1; i <= cnt; i++) {
      for (; r > 1 && M(q[r - 1], q[r], id[i]) <= 0; r--) {
      }
      q[++r] = id[i];
    }
    for (int i = 1; i < r; i++) {
      lx += D(q[i], q[i + 1]);
    }
    lx += D(q[1], q[r]);
    if (lx <= len) {
      if (sum > ans) {
        ans = sum;
        t.clear();
        px = 0;
        for (int i = 1; i <= n; i++) {
          if (vis[i]) {
            t.push_back(i);
          }
        }
        px = len - lx;
      }
    }
    return;
  }
  D(s + 1, sum + v[s], len);
  vis[s] = 1;
  D(s + 1, sum, len + l[s]);
  vis[s] = 0;
}

void I() {
  t.clear();
  for (int i = 1; i <= n; i++) {
    x[i] = y[i] = v[i] = l[i] = q[i] = vis[i] = id[i] = 0;
  }
  px = ans = 0;
}

int main() {
  // freopen(".out", "w", stdout);
  int c = 0;
  while (cin >> n) {
    if (!n) {
      return 0;
    }
    if (c) {
      cout << "\n";
    }
    c++;
    for (int i = 1; i <= n; i++) {
      cin >> x[i] >> y[i] >> v[i] >> l[i];
    }
    D(1, 0, 0);
    cout << "Forest " << c << "\n";
    cout << "Cut these trees:";
    for (int i = 0; i < t.size(); i++) {
      cout << " " << t[i];
    }
    cout << "\n";
    cout << "Extra wood: ";
    printf("%.2lf\n", px);
    I();
  }
  return 0;
}

C:

题意太抽象了，所以这里放一个简要题意：

给你一个凸包，判断在加入任意一个点后但前凸包上的点是否会有至少一个点被踢出去。

\(1\le n\le 1000\)

首先求一遍凸包，然后对于凸包上的每一条边判断该线段上是否至少有 3 个点（包括两端），如果不是就不合法。

然后要注意特判掉一堆非法情况，具体细节见代码。

code:

#include <algorithm>
#include <iostream>

using namespace std;
#define double long double

const int kMaxN = 1e3 + 5;
const double kInf = 1e12;

struct A {
  double x, y;
} a[kMaxN], q[kMaxN];

int r, n, ans, t;

double M(A x, A y, A z) {
  return (y.x - x.x) * (z.y - x.y) - (y.y - x.y) * (z.x - x.x);
}

double S(A x, A y) {
  return (y.y - x.y) / (y.x - x.x == 0 ? kInf : y.x - x.x);
}

double D(A x, A y) {
  return (x.x - y.x) * (x.x - y.x) + (x.y - y.y) * (x.y - y.y);
}

bool C(A x, A y) {
  double v = M(a[0], x, y);
  return v > 0 || !v && D(x, a[0]) < D(y, a[0]);
}

void F() {
  cin >> n;
  a[0].x = a[0].y = kInf;
  for (int i = 1; i <= n; i++) {
    cin >> a[i].x >> a[i].y;
    if (a[i].x < a[0].x) {
      a[0] = a[i];
    } else if (a[i].x == a[0].x) {
      a[0].y = min(a[0].y, a[i].y);
    }
  }
  if (n < 6) { //  !!!!!!!!!!
    cout << "NO\n";
    return;
  }
  sort(a + 1, a + n + 1, C);
  for (int i = 1; i <= n; i++) {
    for (; r > 1 && M(q[r - 1], q[r], a[i]) <= 0; r--) {
    }
    q[++r] = a[i];
  }
  if (r < 3) {  // !!!!!!!!
    cout << "NO\n";
    return;
  }
  for (int i = 1; i <= r; i++) {
    int nxt = i == r ? 1 : i + 1, c = 0;
    for (int j = 1; j <= n; j++) {
      if (q[i].x == q[nxt].x) {
        c += q[i].x == a[j].x && a[j].y >= min(q[i].y, q[nxt].y) && a[j].y <= max(q[i].y, q[nxt].y);
      } else {
        double k = S(q[i], q[nxt]);
        double y = q[i].y + k * (a[j].x - q[i].x);
        c += y == a[j].y;
      }
    }
    if (c < 3) {
      cout << "NO\n";
      return;
    }
  }
  cout << "YES\n";
}

void I() {
  for (int i = 1; i <= n; i++) {
    a[i].x = a[i].y = 0, q[i].x = q[i].y = 0;
  }
  r = n = ans = 0;
}

int main() {
  for (cin >> t; t; t--) {
    F();
    I();
  }
  return 0;
}

标签：cnt,return,浅谈,int,double,kMaxN,vec,计算,几何
From： https://www.cnblogs.com/caoshurui/p/18042059

相关文章

  • 浅谈EK求网络流 & 最小费用最大流
    1.简介：网络流，指的是一种图上问题。首先我们要知道什么是网络。网络的性质如下：有且仅有一个点入度为0，且只有一个点出度为0，我们把入读为0的点叫做源点，出度为0的点为汇点。网络是一个有向图，且有边权。那么流是什么呢？考虑对于下面这个网络：其中\(s\)是源点，\(t\)......
  • 第十二章 如何让计算机“学习”
    当我们谈论计算机“学习”时，我们实际上是指机器学习，这是一种让计算机从数据中学习并自主改进其性能的技术。在阅读《程序是怎样跑起来的》的第十二章后，我对这一领域有了更深入的了解，也对计算机如何学习产生了更多的思考。以下是我对本章的总结：1.什么是机器学习机器学习指的是让......
  • JAVA基础：数组在计算机中的执行原理 多个变量指向一个数组
    程序都是在计算机中的内存中执行的，java程序编译之后会产生一个class文件，这个class文件是提取到内存中的JVM虚拟机中执行的。java为了便于虚拟机这个java程序，也即这个class文件。将虚拟机这块内存区域进行了划分：方法区，栈，堆，  本地方法栈，程序计数器方法区：放编译后的class文件的......
  • 计算复杂性（第八章）
    第八章交互式证明什么是一个好的证明系统天生必须具备的性质？所有正确的能被证明；所有错误的不能被证明；证明者的证明过程和计算量可以很大，但是验证者所需的工作量不应该太大。——Goldwasser,Micali,Rackoff1985什么是交互式证明？可以先假定它指的是一个证明系统，......
  • 如何让计算机学习
    计算机学习是让计算机自己进行学习，在计算机学习中，我们使用学习程序让计算机读取大量数据并根据数据特诊自己进行学习。本章中，针对手写数字识别问题，我们会使用支持向量机算法，我们会使用scikit-learn这个机械学习库，只需要几行代码就可以体验机器学习。SVM是一种机器学习算法，它的全称......
  • 第12章 让计算机“思考”
    程序就如同是计算机执行的各种指令罗列起来的文章。具体来说，控制就是指cpu和各种设备之间配合进行数据的输入输出处理。程序的使用目的，大体可以划分为两类。一类是大家作为工具来使用的程序。另外一个使用目的是用程序来代替执行人类的思考过程。程序也可以有很多用途。比如用程序......
  • 【计算机网络】物理层-编码与调制
    基带信号&宽带信号信道:信号的传输媒介。一般用来表示向某一个方向传送信息的介质,因此一条通信线路往往包含一条发送信道和一条接收信道。基带信号：将数字信号1和0直接用两种不同的电压表示,再送到数字信道上去传输(基带传输)。来自信源的信号,像计算机输出的代表各种......
  • 【计算机网络】物理层传输介质&设备.
    物理层传输介质传输介质也称传输媒体/传输媒介，它就是数据传输系统中在发送设备和接收设备之间的物理通路。传输媒体并不是物理层。传输媒体在物理层的下面，因为物理层是体系结构的第一层，因此有时称传输媒体为0层。在传输媒体中传输的是信号，但传输媒体并不知道所传输的信号代表什......
  • 【计算机网络】物理层-数据交换方式
    为什么要数据交换：减少链路电路交换原理：在数据传输期间，源结点与目的结点之间有一条由中间结点构成的专用物理连接线路，在数据传输结束之前,这条线路一直保持。交换的阶段：建立连接（呼叫/设备间逐个地电路建立）通信（数据传输）释放连接（拆除电路）特点:独占资源,用户始终占用端到......
  • 2024-02-29-Linux高级网络编程(1-计算机网络概述)
    1.计算机网络概述1.1计算机发展简史最早的广域网：在通信双方或多方之间，通过电路交换建立电路连接的网络。1.1.1电路交换特点建立链接->使用链接->释放链接物理通路被通信双方独占1.1.2电路交换适用于电话网​计算机数据是突发式出现在数据链路上的,而电路交......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99