1.简介：

网络流，指的是一种图上问题。首先我们要知道什么是网络。

网络的性质如下：

1. 有且仅有一个点入度为 0，且只有一个点出度为0，我们把入读为 0 的点叫做源点，出度为 0 的点为汇点。

2. 网络是一个有向图，且有边权。

那么流是什么呢？

考虑对于下面这个网络：

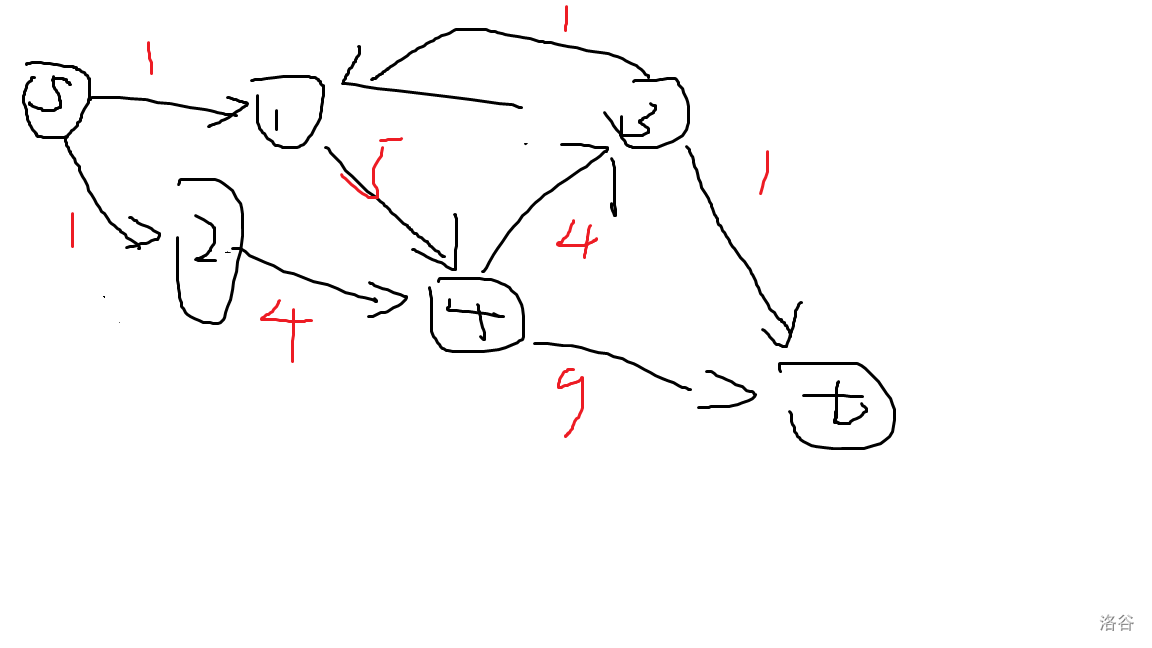
其中 \(s\) 是源点，\(t\) 是汇点。

我们把一条边看成一个水管，边权就是水管的容量，那么一条从 \(s\) 到 \(t\) 的路径就是一条流，而这条流的流量就是这条路径流量最小的那条边。

对于最大流问题，我们要求的其实是所有 \(s\) 到 \(t\) 的所有路径的流量的总和最大是多少。

PS：一条边可以被多条路径经过，但每次流过的水量的总和不能超过其边权。

还有一个定义：增广路，虽然这个名字很高级，但其实就是指一条 \(s\) 到 \(t\) 的流。。。。

2.最大流：

模板题

知道了最大流的定义，我们很显然就可以想到一种暴力算法。
直接从 \(s\) 开始爆搜出每一条路径，到达 \(t\) 后把所有经过的边减去流量，然后答案加上流量。

但这样就有了一个问题：第一次找到的路径径不一定是最优的。

怎么理解这句话呢? 如图：

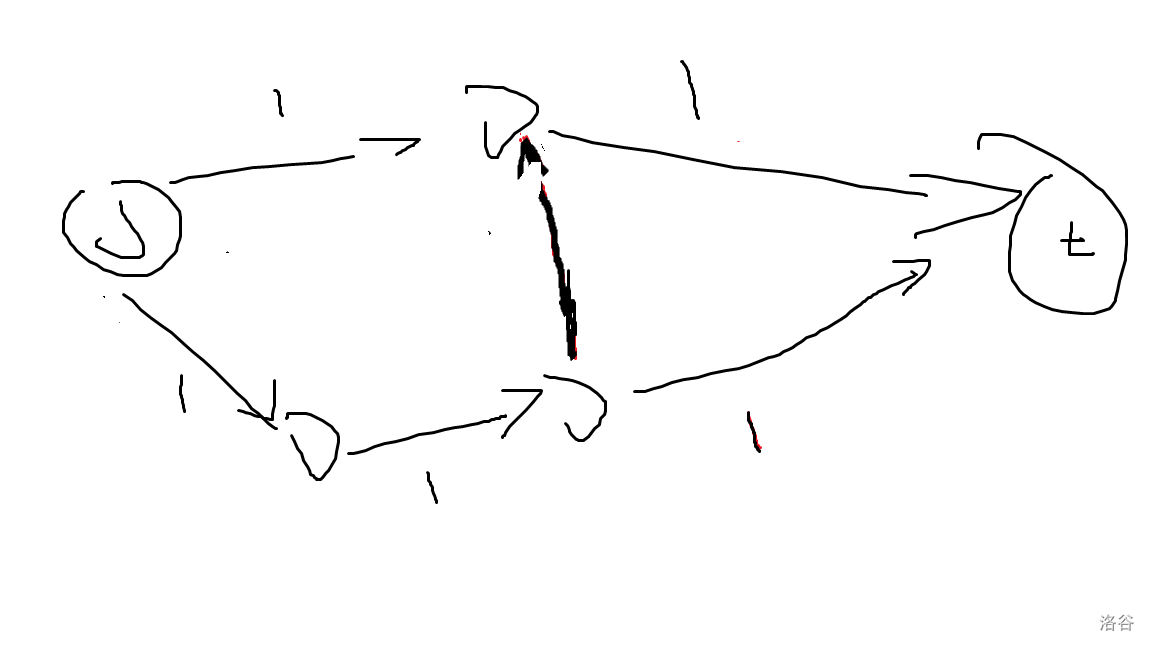
我们考虑在这张图上跑网络流。

显然，最优情况是这样的：

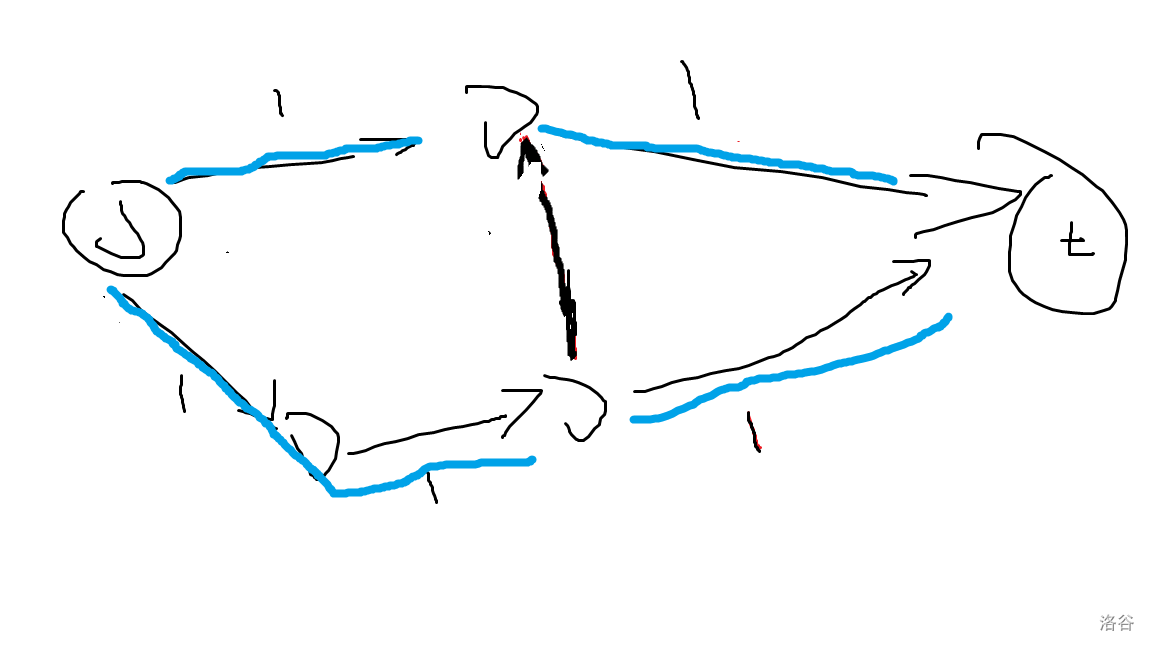
这种路径答案为 2（蓝色路径是最优路径）

但是用上述算法可能会出现这种情况：

这种情况答案为 1。

所以我们要避免第二种情况。

首先想到的肯定是遇到这种路径时尝试撤销这条流，然后回复该边的流量，但这样时间会爆。

这时要用一个很神奇的东西----反向边。

对于每条边我们建一个反向边。
初始时，这条边的容量为 0，代表着所对应的正向边减少了 0，然后每次正向边减少容量反向边就增加容量。

考虑为什么加上反向边后就可行了。

其实我也不会。

我们可以感性理解一下：

如图，一条蓝色的流在过程中遇到了红色的流：

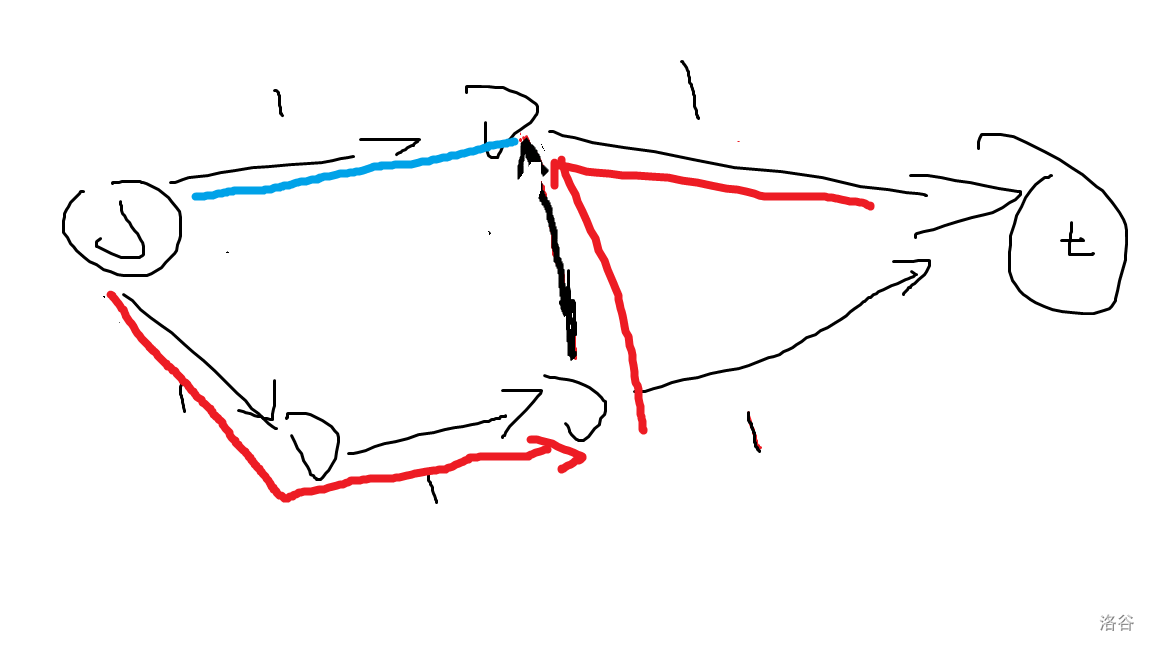
如果没有反向边，就不能流了。
但有了反向边，就可以把红色的流撤回去，如图：

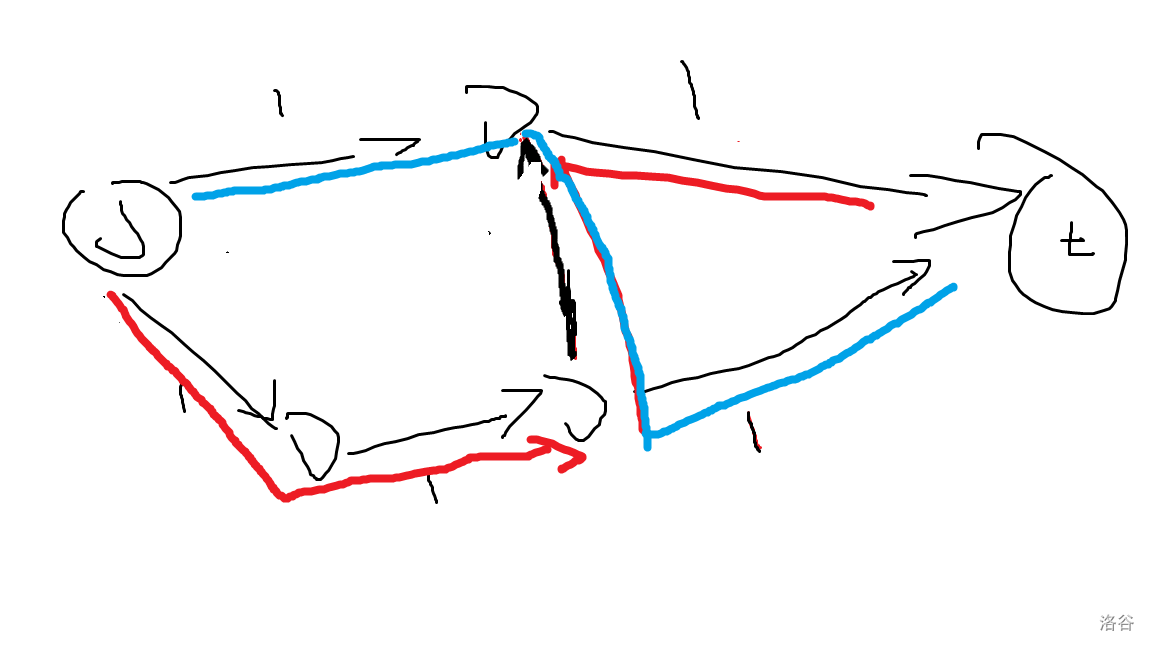
就得到了两条流。

链接生活实际我们可以知道：

其实反向边就相当于这条水管反着流来了 \(x\) 的水，那么原来正向水管中的流量就减少了 \(x\)。

再观察上图我们可以发现：

其实蓝色和红色的路径就相当于下图中的路径：

所以这个算法是正确的。

那么我们再捋一下思路；

1. 用 BFS 或 DFS 随便搜一条 \(s\) 到 \(t\) 的路径。

2. 把路径上的所有值都减去当前路径能经过的最大流量，并把每条边的反向边增加最大流量，答案也增加。

3. 重复 1 和 2 操作。

这样就可以求出最大流了。

CODE（BFS）:

struct D {
  int pre, id;  // 从pre节点来的，经过的id边
} p[kMaxN];

long long q[kMaxN], vis[kMaxN], n, m, s, t, ans;
int nxt[kMaxM], to[kMaxM], val[kMaxM], h[kMaxM], st = 1;

void add(int u, int v, int w) {  //  链式前向星建图
  ++st, nxt[st] = h[u], to[st] = v, val[st] = w, h[u] = st;
}

bool bfs() {  //  bfs 找路径
  int l = 1, r = 0;
  for (int i = 1; i <= n; i++) {
    vis[i] = 0;
    p[i] = {-1, -1};
  }
  for (q[++r] = s, vis[s] = 1; l <= r; l++) {
    int x = q[l];
    if (x == t) {
      return 1;
    } else {
      for (int i = h[x]; i; i = nxt[i]) {
        int v = to[i];
        if (!vis[v] && val[i] > 0) {
          vis[v] = 1;
          q[++r] = v;
          p[v] = {x, i};  //  记录是从哪里来的
        }
      }
    }
  }
  return 0;
}

int EK() {
  while (bfs()) {  //  能够找到增广路
    int x = t, y = 1e9;
    for (; x != s; x = p[x].pre) {  //  找到瓶颈
      y = min(y, val[p[x].id]);
    }
    x = t;
    for (; x != s; x = p[x].pre) {  //  改变流量
      val[p[x].id] -= y, val[p[x].id ^ 1] += y;
    }
    ans += y;
  }
  return ans;
}

DFS：

struct D {
  int pre, id;  // 从pre节点来的，经过的id边
} p[kMaxN];

long long q[kMaxN], vis[kMaxN], n, m, s, t, ans;
int nxt[kMaxM], to[kMaxM], val[kMaxM], h[kMaxM], st = 1;

void add(int u, int v, int w) {  //  链式前向星建图
  ++st, nxt[st] = h[u], to[st] = v, val[st] = w, h[u] = st;
}

bool dfs(int u) {
  if (u == t) {
    return 1;
  }
  bool vs = 0;
  for (int i = h[u]; i; i = nxt[i]) {
    int v = to[i];
    if (val[i] > 0 && !vis[v]) {
      vis[v] = 1;
      p[v] = {u, i};
      vs |= dfs(v);
    }
  }
  return vs;
}


int EK() {
  while (dfs(s)) {  //  能够找到增广路
    int x = t, y = 1e9;
    for (; x != s; x = p[x].pre) {  //  找到瓶颈
      y = min(y, val[p[x].id]);
    }
    x = t;
    for (; x != s; x = p[x].pre) {  //  改变流量
      val[p[x].id] -= y, val[p[x].id ^ 1] += y;
    }
    ans += y;
    fill(vis + 1, vis + n + 1, 0);
  }
  return ans;
}

这里有个小技巧。存边的时候最好是用链式前向星存，然后从 2 开始编号，这样就可以用编号异或 1 来找到反向边了。

还有就是一般建议写广搜（但是深搜也要练，因为 Dinic 要用），因为广搜会自动找到最短的一条路径，减少退流的次数。

最小费用最大流：

模板题

顾名思义，这个问题让你求解的就是在流量最大的情况下找到费用最小的方案。

那么我们该如何选择路径才能让费用最小呢？

我们既然要求费用最小，也就是边权，那么自然而然就可以想到 我们要求出原图的最短路。

对于正的边，其边权就是费用，但 反向边的边权是费用的相反数。为什么呢？

我们可以再次感性理解一下。

我们把一个点的流量通过花费一定费用到另一个点看作是一个人花钱买了票从一个地方到另一个地方。
而反向边就想到与这个人不想去那个地方了，所以要退票，也就是加上 \(-w\) 元。

所以我们把在网络流找路径的时候用的 BFS 或 DFS 换成 SPFA （Dijkstra 解决不了负边权，但是好像有人用势能 Dijkstra 过了（？ ），然后按照最大流的步骤来就好了。

网络流的基础技巧之---拆点

拆点是一种很常见但上限很高的技巧，可以把很多复杂问题转换为网络流问题。

举个栗子

首先我们很容易想到把第 \(i\) 个人和第 \(j\) 个工作之间连一条流量为 1（代表只能一个人只能做一次这个工作），费用为 \(c_{i,j}\) 的边，再让源点向所有人连边，工作向汇点连边，然后在上面跑最小费用流和最大费用流就好了。

但是这样会有一个问题 每个人只能做一个工作，且一个工作只能被一个人做，但如果用上述做法就可能无法满足。

那么我们可以把所有的人和工作都拆成一个入点和一个出点，再在入点和出点间连一个费用为 0 且流量为 1 的边即可。