一、割点、桥基本概念
给定无向图 \(G=(V,E)\)。
对于一个点 \(u \in G\) ,删除一个节点 \(u\)与该节点所有相连的边后,该图不连通,则称点 \(u\) 为割点。
对于一条边\(\{U,W\} \in G\),删除一条边 \(\{U,W\}\) 后,该图不连通,则称边 \(\{U,W\}\) 为桥。
二、暴力算法
对于割点,枚举每个点,看删去这个点后整个图是否连通,若不连通则此点为割点。
对于桥,枚举每条边,看删去这条边后整个图是否连通,若不连通则此边为桥。
朴素做法时间复杂度: \(O(n(n+m))\),复杂度极高。
三、Tarjan 算法
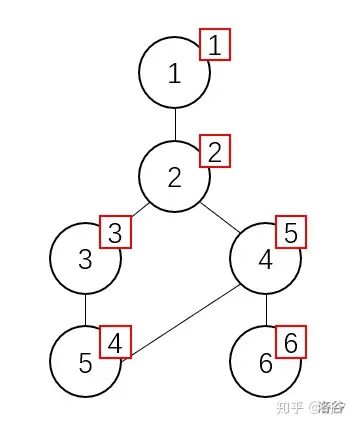
定义 \(dfn[i]\) 表示节点 \(i\) 的 dfs 序。如图:
定义 \(low[i]\) 表示节点 \(i\) 通过返祖边和绕路,能到达的节点里最小的 dfn 值。如图:
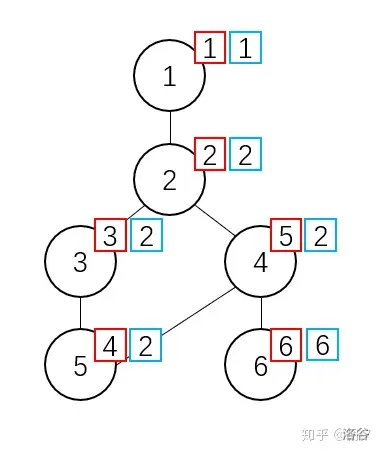
(蓝框数字表示 \(low\),红框数字表示 \(dfn\))
那么问题转化为 \(low\) 的求法。
dfs 过程中,正在节点 \(u\),有边 \((u,v)\),有两种情况:
- \(vis[v]=0\),代表 \(v\) 未被遍历过,则 \(v\) 为 \(u\) 的子节点。则 \(v\) 作为 \(u\) 的子节点,一定会对 \(u\) 做出贡献:
(即如果子节点能到达更小 \(dfn\) 的点,点 \(u\) 也一定能沿着子节点到达)
- \(vis[v]=1\),代表 \(v\) 已经被遍历过,则 按照 dfs 的规律,\(dfn[v]<dfn[u]\),则边 \((u, v)\) 为一条从 \(u\) 到 \(v\) 的返祖边。此时,
(即用 \(u\) 已经搜索到的最小 \(dfn\) 的节点与 \(v\) 节点进行比较)
四、割点的判定
-
对于根节点,若有两棵及以上的子树,则根节点为割点。
-
对于非根节点 \(u\),若其子树中任意一个节点 \(v\) ,均满足
则说明该节点为割点。因为一旦去除 \(u\),则 \(u\) 的子树与其他节点并不连通。
五、桥的判定
- 对于边 \(\{U,W\}\),若 \(w\) 的子树中任意一个节点 \(v\) ,均满足
则说明该边为割边。因为一旦去边 \(\{U,W\}\),则 \(w\) 的子树与其他节点并不连通。
参考核心代码:
void tarjan(int x){
dfn[x]=low[x]=++num;
int f=0;
for (int i=head[x]; i; i=nxt[i]){
int y=ver[i];
if(!dfn[y]){
tarjan(y);
low[x]=min(low[x], low[y]);
if(low[y]>=dfn[x]){ //求割点,如果是割边换成low[y]>dfn[x]
f++;
if(x!=root||f>1) cut[x]=1;
}
}
else low[x]=min(low[x], dfn[y]);
}
}