首页 > 其他分享 >【学习笔记】网络流与二分图初步

【学习笔记】网络流与二分图初步

时间：2024-02-05 09:25:12浏览次数：35  
标签：二分 limits 增广 int sum 笔记 初步 流量

网络流与二分图初步

我们约定，对于有向图 \(G = (V,E)\)，分析复杂度时 \(m = |E|, n = |V|\)。
在分析时间复杂度时，网络流的实际表现基本都优于其理论上的时间复杂度表现。

I 概念

（1）网络流：

在一个有向带权图上（不考虑自环和重边），与最短路类似，我们定义一个源点 \(s\) 和一个汇点 \(t\)。从源点出发，流（flow） 通过各条路径流向汇点，其中，流的大小就成为 流量，
路径上边权就代表着该条边容许通过的最大流量，也称为 容量（Capacity）。就像水流过不同粗细的管道时，水流的大小取决于最细的那根管道一样，每条路径能流过的最大的流量就取决于路径上边容量的最小值，也就是说，该路径上的流量严格不大于该路径上的任意边权值。

使用数学的方法定义：我们定义对于有向图 \(G = (V,E)\)， 边 \((u,v)\) 的容量记为 \(c(u,v)\)， \(f(u,v), u \in V, v \in V\) 为从 \(u\) 到 \(v\) 结点的一个流函数，其中满足：

  1. 容量限制： 每条边流过的流量不大于该条边的容量。 $$f(u,v) \leqslant c(u,v)$$

  2. 流量守恒： 从一个非源汇结点流出的总流量等于流入这个结点的总流量。 $$\sum \limits_{v \in V}f(v, u) = \sum \limits_{v \in V} f(u, v)$$

  3. 斜对称性： 反向边流量与正向的流量相反。$$f(u,v) = -f(v, u)$$

我们称整条网络各条路径的流量之和等于这个网络的流量，这个流量的最大值叫做 最大流。每条边的容量减去流过的流量为剩余容量 \(c_f(u,v) = c(u,v) - f(u,v)\)，流完之后，每条边由剩余容量组成的图叫做 残存网络， 记为 \(G_f\)，特别地，当剩余容量为 \(0\) 时，我们并不将这条边加入到残存网络中。

（2）增广路：

如果我们动态地看待流的过程，我们发现对于一条边，流是可叠加的，即全局的流可以多次地流经一条边，只要保证这些流的总流量不大于这条边的容量即可。我们一次一次地从源点流向汇点，每次将各边容量减去流量得到残存网络，然后再在残存网络上寻找网络流，就是将这个流拆开的过程。每次在 \(G_f\) 上寻找到的从源点 \(s\) 到 \(t\) 的路径称为 增广路，寻找增广路的过程就成为 增广。

（3）网络流的割：

将流网络的点集 \(V\) 分为两部分，一部分包含源点 \(s\)，另一部分包含汇点 \(t\)。记 \(G = (V, E)\) 的一个割为 \((S,T)\)，其中要求 \(s \in S, \ t \in T, \ T = V - S\)。

记所有横跨切割的流量 \(f(S, T) = \sum \limits_{u \in S} \sum \limits_{v \in T} f(u,v) - \sum \limits_{u \in S} \sum \limits_{v \in T} f(v,u)\)

记所有横跨切割的边容量之和为这个割的容量 \(c(S,T) = \sum \limits_{u \in S} \sum \limits_{v \in T} c(u,v)\)。所有割的容量最小值为这个网络的 最小割。

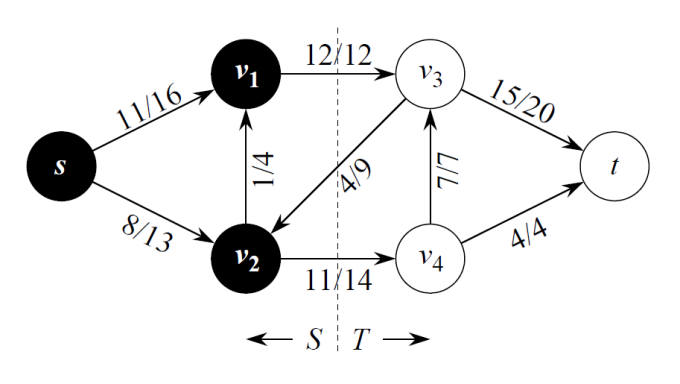
piQS69e.md.png

例：这里是流量图。横跨切割的流量 \(f(S,T) = f(v_1, v_3) + f(v_2, v_4) - f(v_3, v_2) = 12 + 11 - 4 = 19\)， 割的容量 \(c(S,T) = c(v_1, v_3) + c(v_2, v_4) = 12 + 4 = 26\)。

（4）二分图：

如果一个无向图 \(G = (V, E)\)，如果点集 \(V\) 被划成了不相交的两部分 \(L,R\)，且两部分点集没有内部的连边，则称其为 二分图。

对于二分图的一个边集 \(M \in E\)，点集 \(S \in V\)：

  1. 如果 \(M\) 中任意两条边没有公共顶点，则称 \(M\) 是二分图的的一个匹配。
  2. 如果二分图的所有边至少有一个在 \(S\) 中，那么则称 \(S\) 为二分图的一个点覆盖。
  3. 如果 \(S\) 中任意两点都没有边直接相连，则称 \(S\) 为二分图的一个独立集。

II 网络流算法

经过前面的铺垫，我们发现一个流可以拆为很多流的叠加，那么反过来，我们要寻找最大流，其实就是在寻找很多流的组合，使这些流的总流量最大。可以看出看出，一个从源点到汇点的流最基本的就是一条简单路径上的流，其实也就是前面提到的增广路。

最大流的算法基于一个基本的过程 Floyd-Fulkerson：每次不断地寻找增广路，同时建构反向边用以抵消错误的增广路，直到找不到增广路为止，计算此时的答案。

基于这个过程，无论如何寻找增广路，复杂度总不会超过 \(O(m|f|)\)（其中 \(|f|\) 为最大流的大小，可能极大）。

其次的 Edmonds-Karp 算法是 FF 的 BFS 版本，时间复杂度 \(O(nm^2)\)。

最后也是最常用的 Dinic 算法在 FF 基础上加入了分层网络的概念，BFS 搭配 DFS 剪掉了很多枝，具有不错的时间复杂度 \(O(n^2m)\)。

同时我们给出一个基本定理，将在 II/5.算法分析 中证明。

最大流最小割定理： \(f\) 是 \(G = (V,E)\) 中的一个流，以下三者等价：

  1. \(f\) 是 \(G\) 的最大流；

  2. 残存网络 \(G_f\) 不包括任何增广路径；

  3. \(|f| = c(S,T)\)，其中 \((S,T)\) 是网络的最小割。我们就能通过最大流算法同时得到网络的最小割，再跑一遍 BFS 就能得到最小割的方案。

1. Floyd-Fulkerson（寻找增广路）

FF 是解决最大流问题的基本思想，该方法保证时间复杂度下限为 \(O(m|f|)\)。由最大流最小割定理，FF 的算法正确性也就得证了。

方法：

  1. 找到一条增广路，并计算出这条增广路上的流量，流量为这条路径上剩余容量的最小值。
  2. 对于增广路的每条边 \((u,v)\)，使 \(c_f(u,v) = c_f(u,v) - f(u,v)\)；并对于每条边的反向边（初始容量为 \(0\)），使 \(c_f(v,u) = c_f(v,u) + f(u,v)\)。
  3. 重复 1,2 的过程，直到找不到增广路。

2. Edmonds–Karp（BFS 实现 FF 增广）

找增广路时使用 BFS，其他的和 FF 一致。

时间复杂度： \(O(nm^2)\)。

代码：

#include<bits/stdc++.h>
using namespace std;
const int MAXN = 5050;
const long long INF = 0x7f7f7f7f;
int lk[MAXN], ltp;
struct Node{
    int y, nxt;
    long long cap; // 剩余容量
}e[MAXN << 1]; // 牢记两倍边空间！！因为要建反向边
void add(int x, int y, long long cap)
{
    if(lk[x] == 0 && e[1].y != x) lk[x] = -1; 
    e[ltp] = {y, lk[x], cap};
    lk[x] = ltp, ltp++; 
}
/** 
 * 反向边的存储：e[i] 是一条原来的边的话，保证 e[i ^ 1] 是这条边的反向边
 * 那么链式前向星就要发生改动：邻接链表的末尾标记要初始化 -1，
 * 否则 e[0] 会引发歧义。
*/
int n, m, s, t, rt[MAXN];
long long flow[MAXN], ans; 
// 点数，边数，源点，汇点，当前增广路下标数组，
// 当前增广路 f(s, i) 流量，最终总流量
/** 
 * rt[]的存储方式：从后往前存增广路的上一个元素，
 * 这里注意存的是链式前向星的边下标
*/
bool BFS()
{
    bool vis[MAXN];
    fill(vis + 1, vis + 1 + n, 0); // 标记数组，防止成环
    queue<int> q;
    q.push(s);
    flow[s] = INF, vis[s] = 1;
    while(!q.empty()){
        int pre = q.front();
        q.pop();
        for(int i = lk[pre]; i != -1; i = e[i].nxt){
            if(vis[e[i].y] || e[i].cap == 0) continue;
            vis[e[i].y] = 1, rt[e[i].y] = i;
            flow[e[i].y] = min(flow[pre], e[i].cap);
            q.push(e[i].y);
            if(e[i].y == t) return true;
        }
    }
    return false;
}
void EdmondsKarp()
{
    for(;;){
        bool flag = BFS();
        if(!flag) return;
        for(int i = t; i != s; i = e[rt[i] ^ 1].y){
            e[rt[i]].cap -= flow[t];
            e[rt[i] ^ 1].cap += flow[t];
        }
        ans += flow[t];
    }
}
int main()
{
    scanf("%d%d%d%d", &n, &m, &s, &t);
    for(int i = 1; i <= m; i++){
        int x, y;
        long long cap;
        scanf("%d%d%lld", &x, &y, &cap);
        add(x, y, cap);
        add(y, x, 0); // 建反向边
    }
    EdmondsKarp()
    printf("%lld", ans);
    return 0;
}

3. Dinic （在分层网络上的增广路）

一些基本概念：

  1. 层次图：在残存网络 \(G_f\) 上跑一边 BFS, BFS 中只保留每一层流向下一层的边，这些边组成了一个层次图 \(G_L\)。

  2. 阻塞流：在一个图中，不断进行增广直至无法增广出新路（不限定增广的方式，只要进行增广即可），此时得到的流称为阻塞流 \(f_B\)。最大流一定是阻塞流，但阻塞流不一定是最大流。阻塞流显然要比一条增广路更优，因为它肯定是多条增广路的组合。

方法：

  1. 在 \(G_f\) 上 BFS 出当前的分层图 \(G_L\)。

  2. 使用 DFS 在 \(G_L\) 上找到一条阻塞流 \(f_B\)。

  3. 将 \(f_B\) 计入总贡献，并依靠其更新 \(G_f\)

重复上述过程直到 \(G_f\) 上无法进行 BFS（不连通）。

DFS 寻找阻塞流也很细节。

弧优化： DFS 中，枚举某一结点的某一出边时，由于寻找阻塞流的特性，我们会榨干这条边的价值。回溯之后，寻找新的阻塞流时可能还会枚举到这个节点，这时已经被榨干的出边就不再用遍历了，这样我们 DFS 图的复杂度就降到了 \(m\)。

注意当前弧优化中标记的问题！
当前弧要标记在最后一个枚举到的出边上！。在 DFS 遍历出边表时，
如果跑完出边后流入流量还有剩余，说明这条边已经尽力了；
但如果跑完这条出边后流入的流量没有剩余，
这可能意味着流入的流量太小了，这条出边还没有发挥出它的实力，
下一次还得接着跑它，所以当前弧不要标记在 for() 括号里！

时间复杂度： \(O(n^2m)\)。

代码：

#include<bits/stdc++.h>
using namespace std;
const int MAXN = 5050;
const long long INF = 0x7f7f7f7f;
int lk[MAXN], ltp;
struct Node{
    int y, nxt;
    long long cap; // 剩余容量
}e[MAXN << 1]; // 牢记两倍边空间！！因为要建反向边
void add(int x, int y, long long cap)
{
    if(lk[x] == 0 && e[1].y != x) lk[x] = -1; 
    e[ltp] = {y, lk[x], cap};
    lk[x] = ltp, ltp++; 
}
int n, m, s, t, dpt[MAXN], cur[MAXN];
long long ans; 
// 点数，边数，源点，汇点，当前结点的分层图深度，当前弧标记
// 当前增广路 f(s, i) 流量，最终总流量
bool BFS()
{
    fill(dpt + 1, dpt + 1 + n, 0); // 标记数组，防止成环
    queue<int> q;
    q.push(s);
    dpt[s] = 1, cur[s] = lk[s];
    while(!q.empty()){
        int pre = q.front();
        q.pop();
        for(int i = lk[pre]; i != -1; i = e[i].nxt){
            if(dpt[e[i].y] || e[i].cap == 0) continue;
            cur[e[i].y] = lk[e[i].y], dpt[e[i].y] = dpt[pre] + 1;
            q.push(e[i].y);
            if(e[i].y == t) return true;
        }
    }
    return false;
}
long long DFS(int pre, long long flow)
{
    if(pre == t) return flow;
    long long rtcap, rtflw = 0; 
    // 当前出边后阻塞流流量，该点所有出边阻塞流总流量 
    for(int i = cur[pre]; i != -1 && flow > 0; i = e[i].nxt){
        cur[pre] = i; // 当前弧要标记在 for 循环里面，最后一条枚举到的出边上
        if(e[i].cap == 0 || dpt[pre] + 1 != dpt[e[i].y]) continue;
        rtcap = DFS(e[i].y, min(flow, e[i].cap));
        if(rtcap == 0) continue;
        e[i].cap -= rtcap, e[i ^ 1].cap += rtcap;
        rtflw += rtcap, flow -= rtcap;
    }
    return rtflw;
}
void Dinic()
{
    while(BFS())
        ans += DFS(s, INF); 
}
/** 
 * DFS 中的细节很多：
 * 传入的形参 flow 实际上是流到结点 pre 时的实时流量
 * 现在要找阻塞流，那么就要把这些流量用完，
 * 如果用不完就返回 pre 后面层次能用的流量最大值。
 * 当前弧的作用就在这儿，每次从上层流到 pre 后，pre 下
 * 层的所有出边都竭尽全力地消耗流量，那么消耗殆尽的出边
 * 是不参与后面的阻塞流贡献的，所以每条边最多会被枚举 1 次
*/
int main()
{
    scanf("%d%d%d%d", &n, &m, &s, &t);
    for(int i = 1; i <= m; i++){
        int x, y;
        long long cap;
        scanf("%d%d%lld", &x, &y, &cap);
        add(x, y, cap);
        add(y, x, 0); // 建反向边
    }
    Dinic();
    printf("%lld", ans);
    return 0;
}

4. 最小割问题

根据 最大流最小割定理，我们发现只要求出了网络最大流，那么该网络的最小割也就得到了。那么跑一遍 Dinic 就行了。

如果想要进一步求出满足最小割的 \((S, T)\) 方案。那么从原点跑一边 DFS，能跑到的点就在 \(S\) 中，跑不到的点就在 \(T\) 中。

5. 费用流问题

网络 \(G = (V, E)\)，边 \((u, v)\) 有容量 \(c(u,v)\) 和单位流量费用 \(w(u, v)\)，这意味着当这条边流过 \(f(u,v)\) 时，还要花费 \(f(u,v) \times w(u,v)\) 的费用。

这里我们解决 最小费用最大流问题

SSP 方法： 每次寻找流路径上单位费用和最小的增广路增广，直到图上不存在增广路为止。即在原先的 EK/Dinic 算法的基础上，寻找增广路时使用最短路算法。

值得注意的是，由于费用可能存在负数，不能裸着跑 Dijkstra。

Primal-Dual 原始对偶算法： 既然不能跑 Dijkstra，而 SPFA 又太慢，那能不能把边权变成正的，再跑 Dijkstra 找增广路呢？答案是可行的。我们采用上一篇博客中 Johnson全源最短路 中的方法：

从源点 \(s\) 向所有结点各连一条边权为 \(0\) 的边，跑 \(1\) 遍 SPFA 求出 \(s\) 结点到各个结点的最短路长短分别为 \(h_1 \sim h_n\)，使边 \((u,v)\) 的新费用 \(\hat w_{(u,v)} = w_{(u,v)} + h_u - h_v\)。

增广后因为多了些反边，我们还要对新的 \(\hat w_{(u,v)}\) 进行调整：跑增广路时我们又得到了每个点 \(u\) 到源点 \(s\) 的新的最短路 \(h'_u\)，那么跑完之后我们就将原来的的 \(h_u\) 加上求出来的 \(h'_u\) 即可。

反边建边时也满足斜对称性 \(w(u,v) = -w(v, u)\)，这是因为费用也要能够抵消才行。

时间复杂度： \(O(mn + m \log n |f|)\)。

代码：

#include<bits/stdc++.h>
using namespace std;

typedef long long ll;
const int MAXN = 50050;
const ll INF = 0x7f7f7f7f;

int lk[MAXN], ltp;
struct Node{
    int y, nxt;
    ll cap, w; // 剩余容量，费用
}e[MAXN << 1]; // 牢记两倍边空间！！因为要建反向边
void add(int x, int y, ll cap, ll cost)
{
    if(lk[x] == 0 && e[1].y != x) lk[x] = -1; 
    e[ltp] = {y, lk[x], cap, cost};
    lk[x] = ltp, ltp++; 
}

int n, m, s, t, rt[MAXN];
ll dist[MAXN], h[MAXN], flow, cost; 
// 点数，边数，源点，汇点，当前增广路下标数组，
// 最短路长度，势标记，总流量，总费用；
struct Nd{
    ll d; int p;
    bool operator < (const Nd &x) const{
        return x.d < d;
    }
};
void SPFA()
{
    bool vis[MAXN];
    fill(vis + 1, vis + 1 + n, 0);
    fill(dist + 1, dist + 1 + n, INF);
    fill(h + 1, h + 1 + n, INF); // 这里三个初始化都要牢记
    queue<int> q;
    q.push(s);
    h[s] = 0, vis[s] = 1;
    while(!q.empty()){
        int u = q.front();
        q.pop();
        vis[u] = 0;
        for(int i = lk[u]; i != -1; i = e[i].nxt){
            int v = e[i].y;
            if(e[i].cap != 0 && h[u] + e[i].w < h[v]){
                h[v] = h[u] + e[i].w;
                if(!vis[v]){ q.push(v); vis[v] = 1;}
            }
        }
    }
}
bool Dijkstra()
{
    bool vis[MAXN];
    fill(vis + 1, vis + 1 + n, 0); // 标记数组，防止成环
    fill(dist + 1, dist + 1 + n, INF);
    priority_queue<Nd> q;
    q.push((Nd){0, s});
    dist[s] = 0;
    while(!q.empty()){
        Nd tmp = q.top();
        q.pop();
        int u = tmp.p;
        if(vis[u]) continue;
        vis[u] = 1;
        for(int i = lk[u]; i != -1; i = e[i].nxt){
            int v = e[i].y;
            ll cost = e[i].w + h[u] - h[v];
            if(e[i].cap != 0 && dist[u] + cost < dist[v]){
                rt[e[i].y] = i;
                dist[v] = dist[u] + cost;
                if(!vis[v]) q.push({dist[v], e[i].y});
            }
            /** 注意这里不！能！if(v==t) return，因为这是在跑最短路，松弛
              * (u,t) 不代表着找到了从 s 到 t 的最短路 */
        }
    }
    if(dist[t] == INF) return false;
    return true;
}
// 注意 dijkstra 和 SPFA 的区别，不要把 vis 更改写串了
void Primal_Dual()
{
    SPFA();
    for(;;){
        bool flag = Dijkstra();
        if(!flag) return;
        ll curflow = INF;
        for(int i = 1; i <= n; i++) h[i] += dist[i];
        for(int i = t; i != s; i = e[rt[i] ^ 1].y)
            curflow = min(curflow, e[rt[i]].cap);
        for(int i = t; i != s; i = e[rt[i] ^ 1].y){
            e[rt[i]].cap -= curflow;
            e[rt[i] ^ 1].cap += curflow;
        }
        flow += curflow;
        cost += curflow * h[t]; 
        /** 注意这里 *h[t]，不！要！写成 *dist[t]，因为 h[t] 才代表着 s 到 t
          * 的费用和，而dist[t]不是原始的费用，仅代表着拓扑关系 */
    }
}
int main()
{
    scanf("%d%d%d%d", &n, &m, &s, &t);
    for(int i = 1; i <= m; i++){
        int x, y;
        ll cap, cos;
        cin >> x >> y >> cap >> cos;
        add(x, y, cap, cos);
        add(y, x, 0, -cos); // 注意这里费用是-cos！！
    }
    Primal_Dual();
    cout << flow << " " << cost;
    return 0;
}

6. 算法分析

（1）建反向边的有效性

我们考察这个简单的例子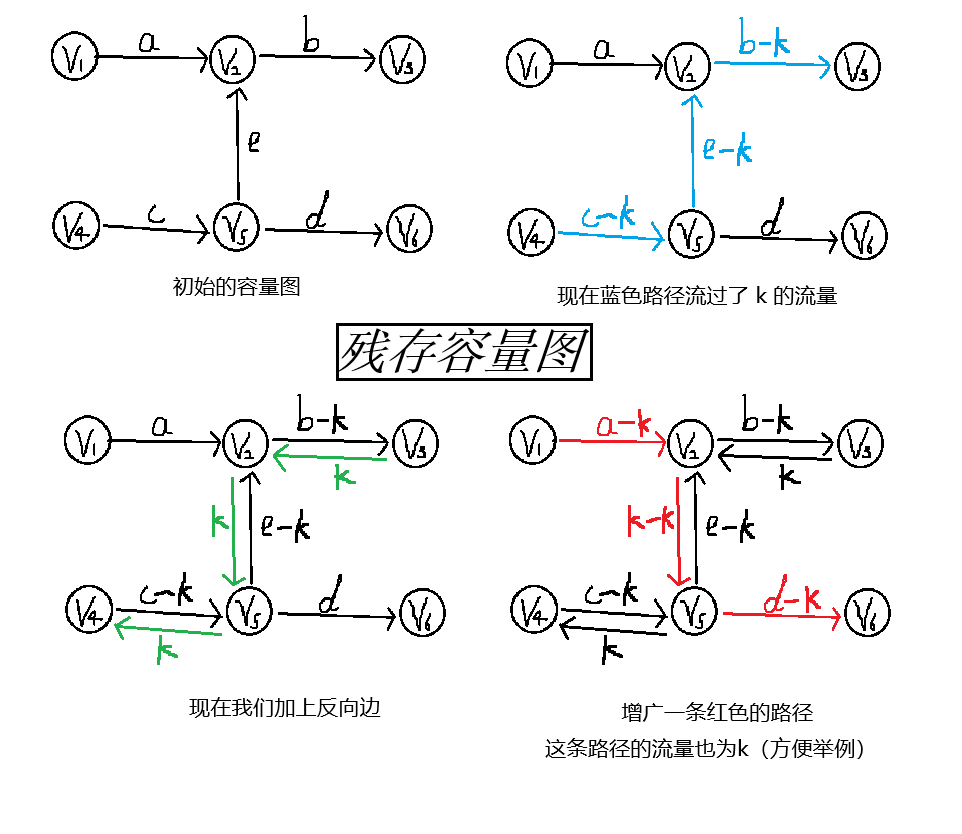： 反向边原理

我们看到，蓝色流很有可能变成一个阻塞流，但是我们这里加入了反向边。在蓝色流完后，我们找到了一条红色的增广路，让我们看看它是如何抵消刚才的操作的：

两次 \(k\) 流量的流，红色流是 \(v_1 \rightarrow v_2 \rightarrow v_5\)，蓝色流是 \(v_5 \rightarrow v_2 \rightarrow v_3\)。综合起来，由于流量相同，中间都有 \(v_2\) 结点作中转，我们可以等效的看为：一支流是 \(v_1 \rightarrow v_2 \rightarrow v_3\)，另一支流 \(v_5 \rightarrow v_2 \rightarrow v_5\)。 发现没有，这个第二支流直接流回了 \(v_5\)，相当于操作被抵消了！这个时候带着 \(k\) 的流量通过反向边流回到 \(v_5\) 结点的红色流恰好可以看作当初刚刚流到 \(v_5\) 的蓝色流。现在的红色流可以为当初的蓝色流可以重新选择一遍了自己的路径了！这时的红色流选择流向 \(v_6\) 结点。如果红色流到了 \(v_5\) 结点后选择流去 \(v_4\) 呢？其实就相当于回到了当初刚刚流到 \(v_4\) 的蓝色流。现在红色流和蓝色流就完全等价了。

这是两次流一样的情况，那两次流不一样呢？实际上，我们可以将流量大的那条流看成流了两次，一次流量和小的流量相等，一次流量是这个较小的流量抵消后的剩余流量（其实就是大流量减去这个较小流量的值）。那么，问题又回到了到了一个流的问题。

（2）最大流最小割定理的证明

引理1： 跨越任何一个切割的流量都等于流的流量。\(\forall (S,T)\)，总有 \(|f| = f(S,T)\)。

引理2： 一个流的流量总不大于任何一个割的容量。\(\forall (S,T)\)，总有 \(|f| \leqslant c(S,T)\)。

引理1的证明： 规定 \(s\) 为源点，\(t\) 为汇点。

由 流量守恒 ，对于任何 \(u \ne s,t\)，我们有 \(\sum \limits_{v \in V} f(u, v) - \sum \limits_{v \in V} f(v, u) = 0\)。

\[\begin{aligned} |f| &= \sum \limits_{v \in V} f(s, v) \\ &= \sum \limits_{v \in V} f(s, v) - \sum \limits_{v \in V} f(v, s)\\ &= \sum \limits_{v \in V} f(s, v) - \sum \limits_{v \in V} f(v, s) + \sum \limits_{u \in S - \{s\}}(\sum \limits_{v \in V} f(u, v) - \sum \limits_{v \in V} f(v, u)) \\ &= \sum \limits_{u\in S}(\sum \limits_{v \in V} f(u, v) - \sum \limits_{v \in V} f(v, u)) \\ &= \sum \limits_{u\in S}\sum \limits_{v \in V} f(u, v) - \sum \limits_{u\in S}\sum \limits_{v \in V} f(v, u) \\ \end{aligned} \]

由于 \(V = S \cup T\)，且 \(S \cap T \ne \varnothing\)，我们将求和中的 \(v\in V\)拆开：

\[\begin{aligned} |f| &= \sum \limits_{u\in S}\sum \limits_{v \in S} f(u, v) + \sum \limits_{u\in S}\sum \limits_{v \in T} f(u, v)- \sum \limits_{u\in S}\sum \limits_{v \in S} f(v, u) - \sum \limits_{u\in S}\sum \limits_{v \in T} f(u, v)\\ \end{aligned} \]

后面两项实际上在字母上是对称的，故而完全相等，可以消去，最后就剩下：

\[\begin{aligned} |f| &= \sum \limits_{u\in S}\sum \limits_{v \in T} f(u, v) - \sum \limits_{u\in S}\sum \limits_{v \in T} f(v, u) = f(S,T) \ \ \ \square \end{aligned} \]

引理2的证明： 根据 引理1 和 容量限制：

\[\begin{aligned} |f| &= \sum \limits_{u\in S}\sum \limits_{v \in T} f(u, v) - \sum \limits_{u\in S}\sum \limits_{v \in T} f(v, u) \\ &\leqslant \sum \limits_{u\in S}\sum \limits_{v \in T} f(u, v) \\ &\leqslant \sum \limits_{u\in S}\sum \limits_{v \in T} c(u, v) = c(S,T) \ \ \ \square \end{aligned} \]

从 引理2的证明 中可以看出，\(|f| = c(S,T)\) 当且仅当：

\[\sum \limits_{u\in S}\sum \limits_{v \in T} f(v, u) = 0，\sum \limits_{u\in S}\sum \limits_{v \in T} f(u, v) = \sum \limits_{u\in S}\sum \limits_{v \in T} c(u, v) \]

这意味割等于流时，所有从 \(S\) 到 \(T\) 的割边 剩余容量 都为 \(0\)，所有 \(T\) 到 \(S\) 的割边剩余容量都为 容量，这也启示了我们寻找最小割方案时的 DFS 的正确性：从 \(s\) 结点开始一定到达不了 \(T\) 中的结点。

引理1同时也说明：流的流量不会超过最小割的容量

最大流最小割定理： \(f\) 是 \(G = (V,E)\) 中的一个流，以下三者等价：

  1. \(f\) 是 \(G\) 的最大流；

  2. 残存网络 \(G_f\) 不包括任何增广路径；

  3. \(|f| = c(S,T)\)，其中 \((S,T)\) 是网络的最小割切割。

最大流最小割定理的证明：

  1. 1 \(\Rightarrow\) 2： 如果残存网络中还存在增广路，那还可以通过这条增广路增加流量，这与 \(f\) 是最大流矛盾，故残存网络中不存在增广路。

  2. 2 \(\Rightarrow\) 3： \(G_f\) 上增广路不连通，意味着一定可以将 \(V\) 分为 \(S,T\) 两个点集，使得 \(S\) 到 \(T\) 中的每条边都是满流的，根据斜对称性，此时 \(T\) 到 \(S\) 的所有连边只能为 \(0\)。又根据 引理2，此时 \(|f| = c(S,T)\)。

  3. 3 \(\Rightarrow\) 1： 根据 引理2，我们总有最大流的流量不会超过最小割的容量，故此时 \(f\) 就是最大流。

（3）FF 增广的时间复杂度下限

考虑如下例子：

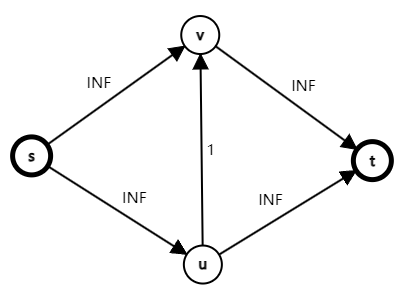
FF时间下限例子

如果随机选择增广路，那么我们来回增广 \(s \rightarrow u \rightarrow v \rightarrow t\)，和 \(s \rightarrow v \rightarrow u \rightarrow t\) （建了反边），那么我们就要重复这个过程 \(INF\) 遍，即增广轮数 \(|f|\)，每次增广 \(m\)，总的复杂度下限就是 \(O(m|f|)\)。

III 二分图

1. 二分图最大匹配

方法（最大流建模）： 设图 \(G = (V, E)\) 被分成了 \(L,R\) 两个点集，我们在图外建一个源点 \(s\)，和一个汇点 \(t\)。

  1. 分别将所有 \(L\) 中的点与 \(s\) 连一个容量为 \(1\) 的的边，
  2. \(R\) 中的点与 \(t\) 连一个容量为 \(1\) 的的边，
  3. \(L\) 到 \(R\) 中原来的边都为 \(\infin\)。

那么在这个新图上找到最大流，问题就解决了。

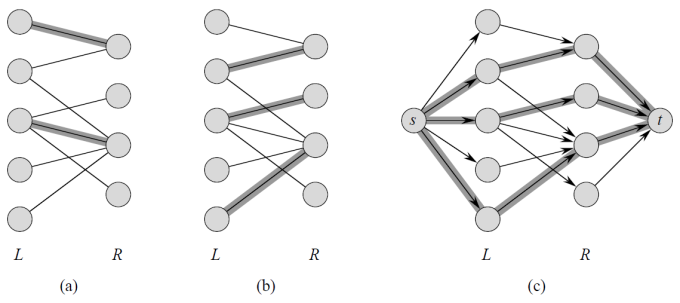[piQlBQA.md.png]

例：如上图，源汇点各连一条容量为 1 的边就限制了 1 个结点只能接到对面点集的 1 个结点上，保证了二分图的匹配。

那么代码跑一边 Dinic 就好了，没有必要放了。

注意：新加边和点之后数据范围可能会发生变化。
各类数组要开大！
使用 fill() 函数初始化时注意传参的范围！

由于容量限制都为 1, 最终的复杂度为 \(O(m \sqrt{n})\)。

2. 二分图的相关性质

（1）König 定理

二分图最大匹配 = 二分图最小点覆盖。

证明： 按照刚才的建模，只需说明二分图的最小点覆盖与网络流的最小割等价，再根据 最大流最小割定理 证明即可。

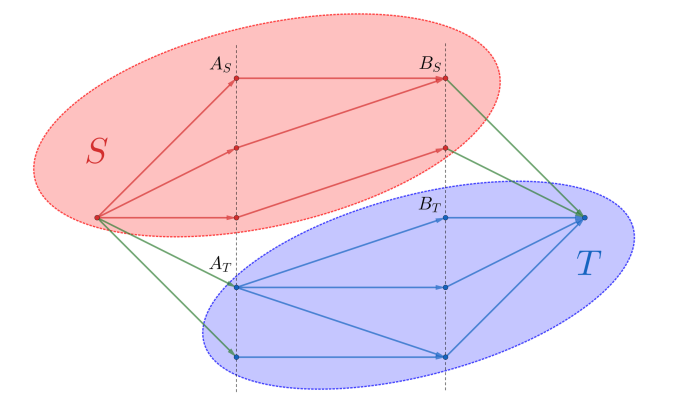
piGkn6x.md.png

这里我们构造 \((S,T)\) 为图的最小割。其中左部图中属于 \(S\) 的点集为 \(A_S\)、属于 \(T\) 的点集为 \(A_T\)，右部图中属于 \(S\) 的点集为 \(B_S\)、属于 \(T\) 的点集为 \(B_T\)，我们断言：\(A_T \cup B_S\) 为二分图的最小点覆盖。

  1. 二分图上不应存在 \(A_S \rightarrow B_T\) 的边，如果存在，那么最小割就是 \(\infin\) （建图时保证的 \(c(A \rightarrow B) = \infin\)），但是最小割等于最大流肯定不是无限大，矛盾。所以只存在 \(A_S \rightarrow B_S\) 和 \(A_T \rightarrow B_T\) 的边。不难发现任意边 \((u,v)\) 都有 \(u \in A_T\) 或 \(v \in B_S\)，故而最小割是二分图的一个点覆盖。
  2. 不难发现此时最小割是 \(\sum\limits_{v\in A_T} c(s, v) + \sum\limits_{u\in B_S} c(u, t)\)，如果还存在更小的点覆盖，那么必然要在 \(A_T \cup B_S\) 中再割掉一个点，但这样最小割也就减小了，不符合前提，故而不存在更小的点覆盖。

（2）二分图的最大独立集 = \(|V|\) - 二分图的最小点覆盖。

解释： 二分图最小点覆盖的补集即为二分图的最大独立集。二分图的点覆盖意味着每条边至少有一个点被选中，也就意味着每条边至多有一个点没被选中。这就说明如果放弃掉原来的点覆盖，选中边另外一侧的点，就能保证每条边只有最多一个点被选中，也就满足了独立集的条件。上面至多至少的条件是等价的，也就永远成立，说明所有独立集都能用点覆盖生成，故而最大独立集为最小点覆盖的补集。

（3）Hall 定理

对于二分图 \(G(L,R,E)\)，和任意 \(L' \subseteq L\) 及所有右部点中与 \(L\) 中的点有边直接相连的点集 \(R'\)，则二分图存在完美匹配（最大匹配等于左右部点集大小）的充要条件是：

\[|L'| \leqslant |R'| \]

标签：二分,limits,增广,int,sum,笔记,初步,流量
From： https://www.cnblogs.com/anjack511/p/18007375/GraphStudy2

相关文章

  • 读千脑智能笔记04_参考系
    1.      大脑中的参考系1.1.        人类出色的认知功能是区分我们与灵长目动物的最显著的特点1.1.1.          只有人类才能使用复杂的语言，制造诸如计算机等复杂的工具，并且能够论证进化、遗传学和民主等概念1.2.        人类大脑新皮质......
  • ES笔记：IK分词器
    ES中文档按照分词进行检索，对于中文，ES默认按照单个字进行分词，非常低效，可以使用专门的中文分词器，如IK分词器。下载：https://github.com/medcl/elasticsearch-analysis-ik/releases安装：在ES的plugins目录下新建一个目录，将下载的IK分词压缩包解压到此目录即可，然后重启ES该分词器便......
  • C++ Primer 学习笔记 PartI C++基础
    Ch1开始略这一章包含控制流，条件，循环，注释，标准IO等内容。对于C语言/ACMC+STL中常见数值的内容不再赘述，仅总结较为不熟悉的内容。PartIC++基础CH2变量和基本类型2.1基本内置类型2.1.1算术类型2.1.1类型转换向unsigned赋超出范围的值，结果取余，对于signed，结果未定义。......
  • 基本知识笔记
    浮点数到定点数：【CO101】计算机组成原理笔记1——定点数转单精度浮点数（SEM）_定点转浮点原理-CSDN博客原码、补码、反码笔记：Verilog--有符号与无符号的加法和乘法运算_veriloga+b=c-CSDN博客是计算机中对数字的二进制表示方法。原码：将最高位作为符号位（0表示正，1表示负），其它......
  • 工程细节笔记
    SDRAM控制器读写非数据流的情况：在某些情况下最后剩下的那一段数据无法达到单次Brust长度，此时应该仲裁决定是否继续读写。这个问题在DDR3需要通过填0去解决，因为预读量远不是一个级别，填零以后通过截断获得有效数据是好的做法。//WR_req  always@(posedgeSys_clkornege......
  • 线段树二分——nc2.4多校_G.新春漫步
    目录问题概述思路分析参考代码做题反思问题概述原题参考G.新春漫步坐标轴上有n个点，初始时每个位置上都有一个坚固程度为a1的障碍物，接下来有m次操作1.将位置p上的障碍物的坚固程度减去x，若减去x后坚固程度小于等于0，则该障碍物消失2.询问一个人从p的位置向右走，最多能走到什么位......
  • [经验] 笔记本怎么重置
    随着社会的快速发展，笔记本电脑在人们的日常生活中扮演着越来越重要的角色，尤其在学习和工作中的应用愈加广泛。然而，因为使用不当或者出现故障，笔记本肯定是少不了需要重置的情况。那么，究竟笔记本怎么重置呢？本文将会对这个话题进行详细阐述。什么是笔记本重置？笔记本重置是指将笔记本电......
  • 【学习笔记】OI 数学学习笔记
    OI数学学习笔记001_整除001.1_整除基础001.1A基本定义整除与因数倍数的定义：设\(a,b\in\mathbb{Z}，b\ne0\)，若存在\(q\in\mathbbZ\)，使得\(a=bq\)，则称\(b\)整除\(a\)，记为\(b\mida\)，此时称\(a\)为\(b\)的因数，\(b\)为\(a\)的倍数.带余除法与余数的......
  • Pandas库学习笔记（6） -- Pandas 基本方法
    Pandas基本方法实例到目前为止，我们了解了三个PandasDataStructures以及如何创建它们。由于它在实时数据处理中的重要性，因此我们将主要关注DataFrame对象，并讨论其他一些DataStructures。方法描述axes返回行轴标签的列表dtype返回对象的dtype。empty如果Series......
  • 代码随想录算法训练营第一天 | 27. 移除元素 | 704. 二分查找
     704.二分查找 已解答简单 相关标签相关企业 给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。示例1:输入:numstarget输出:解释:nums......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99