一. 普通线段树合并
线段树合并就是建立一棵新的线段树保存原有的两棵线段树的信息。
两棵线段树当前要合并的点所表示的区间是一样的。
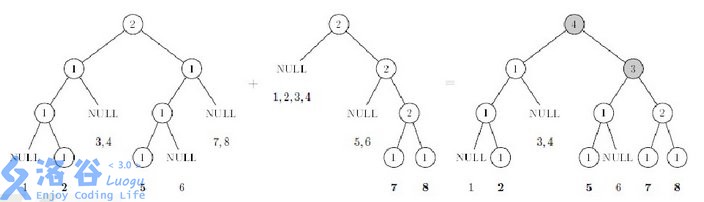
线段树合并的过程很简单。
如果A有p位置,B没有,新的线段树p位置赋成A,返回 A;
如果B有p位置,A没有,新的线段树p位置赋成B,返回 A;
如果合并到叶子结点,按照所需合并A,B,把新线段树上的p位置赋成A,返回 A;
递归左子树,递归右子树;
更新A (当前节点);
返回 A;
以下是一份较为常见的 merge 代码实现。
//l,r表示当前所访问的节点的区间,x,y表示当前节点在A,B两棵线段树中的编号
//这里是将B合并到A上,返回的是A的节点
inline int merge(int x,int y,int l,int r){
if(!x||!y)return x+y;//若A或B没有区间[l,r]这个节点就返回另一个
if(l==r){//merge到了叶子结点
tr[x]=tr[x]+tr[y];//执行合并操作
return x;
}
int mid=(l+r)>>1;
ls[x]=merge(ls[x],ls[y],l,mid);
rs[x]=merge(rs[x],rs[y],mid+1,r);//递归左右子树
pushup(x);
return x;
}
注意:以上做法线段树合并的修改与合并不能同时。
假如对于两棵树 \(x,y\),某个节点 \(u\), 在 \(x\) 中未出现而在 \(y\) 中出现,那么由于最后是合并到 \(x\) 上,所以 \(fa_u\) 的儿子会直接指向 \(y\) 中的 \(u\)。
但是若我们修改了 \(u\),那么 \(y\) 的形态结构就会发生改变。
这种做法在许多题目都是对的是因为 update 与 merge 不同时,或者将询问离线下来。这样若保证了 merge 后不会 update,或者离线询问后从下往上 merge(保证合并后的子树不被修改)。
一个解决方法就是可持久化。
新建一个节点 \(p\) 来表示 \(u\),然后 merge。
这样就使得 \(y\) 子树不会被改变。
inline int merge(int x,int y){
if(!x||!y)return x|y;
int p=++id;
ls[p]=merge(ls[x],ls[y]);
rs[p]=merge(rs[x],rs[y]);
pushup(p);
return p;
}
考虑对于每个点建一棵权值线段树。
树上差分,对于在从 \(u\) 到 \(v\) 的路径加上颜色 \(col\),直接在 \(u,v\) 处加上 \(col\),然后在 \(\text{lca}(u,v)\) 与 \(fa_{\text{lca}(u,v)}\) 的 \(col\) 减一。
这样对于点 \(u\),其所有的 \(col\) 就在其子树中,可以使用线段树合并。
由于是动态开点,所以用一个一维数组 tr[p] 表示动态开点后编号为 \(p\) 的节点。
但是这样无法分清哪些节点是哪棵树,所以加入 rt[u] 表示 \(u\) 所在的权值线段树的根。
维护一个 kx[p] 表示权值线段树中编号为 \(p\) 的节点中出现最多的粮食的编号。
tr[p] 则表示出现最多的粮食的出现次数。
统计颜色时遍历树,从下到上,将 \(u\) 与它儿子 \(v\) 的权值线段树合并,并记录答案。
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+6;
const int M=8e6+7;
const int lim=1e5;
const int lg=18;
struct edge{
int to,nxt;
}e[N<<1];
int n,m,head[N],tot,f[N][lg+1],dep[N],tr[M],kx[M],ls[M],rs[M],ans[N],rt[N],id;
inline void addedge(int u,int v){
e[++tot].to=v;
e[tot].nxt=head[u];
head[u]=tot;
return;
}
inline void predfs(int u,int fa){
dep[u]=dep[fa]+1;
f[u][0]=fa;
for(int i=1;i<=lg;i++)f[u][i]=f[f[u][i-1]][i-1];
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(v==fa)continue;
predfs(v,u);
}
return;
}
inline int lca(int u,int v){
if(dep[u]>dep[v])swap(u,v);
for(int i=lg;i>=0;i--)if(dep[f[v][i]]>=dep[u])v=f[v][i];
if(u==v)return u;
for(int i=lg;i>=0;i--){
if(f[u][i]!=f[v][i]){
u=f[u][i];
v=f[v][i];
}
}
return f[u][0];
}
inline void pushup(int p){
if(tr[ls[p]]>=tr[rs[p]]){
tr[p]=tr[ls[p]];
kx[p]=kx[ls[p]];
}
else{
tr[p]=tr[rs[p]];
kx[p]=kx[rs[p]];
}
return;
}
inline void update(int &p,int l,int r,int col,int val){
if(!p)p=++id;
if(l==r){
tr[p]+=val;
kx[p]=col;
return;
}
int mid=(l+r)>>1;
if(col<=mid)update(ls[p],l,mid,col,val);
else update(rs[p],mid+1,r,col,val);
pushup(p);
return;
}
inline int merge(int x,int y,int l,int r){
if(!x||!y)return x+y;
if(l==r){
tr[x]=tr[x]+tr[y];
return x;
}
int mid=(l+r)>>1;
ls[x]=merge(ls[x],ls[y],l,mid);
rs[x]=merge(rs[x],rs[y],mid+1,r);
pushup(x);
return x;
}
inline void dfs(int u,int fa){
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(v==fa)continue;
dfs(v,u);
rt[u]=merge(rt[u],rt[v],1,lim);
}
ans[u]=kx[rt[u]];
if(!tr[rt[u]])ans[u]=0;
return;
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<n;i++){
int u,v;
scanf("%d%d",&u,&v);
addedge(u,v);
addedge(v,u);
}
predfs(1,0);
for(int i=1;i<=m;i++){
int u,v,o,col;
scanf("%d%d%d",&u,&v,&col);
o=lca(u,v);
update(rt[u],1,lim,col,1);
update(rt[v],1,lim,col,1);
update(rt[o],1,lim,col,-1);
update(rt[f[o][0]],1,lim,col,-1);
}
dfs(1,0);
for(int i=1;i<=n;i++)printf("%d\n",ans[i]);
return 0;
}
这道题就是之前所说的可持久化 merge 方法。
首先 \(a\) 和 \(b\) 都是 \(c\)的祖先。
考虑 \(a,b\) 之间的祖先关系。
- \(b\) 是 \(a\) 的祖先。
那么 \(b\) 就是 \(a\) 的父亲往上的一条链,有 \(\min\{k,dep_a-1\}\) 个节点。\(c\) 在 \(a\) 子树中随便取。总方案数 \(\min(k,dep_a-1)*(sz_a-1)\)。
- \(b\) 是 \(a\) 的后代。
那么 \(b\) 在 \(a\) 的子树中随便取,\(c\) 继续在 \(b\) 的子树中随便取。
方案数为 \(\displaystyle \sum_{dep_a+1\le dep_u\le dep_a+k}(sz_u-1)\)。
那么考虑建权值线段树下标表示深度。
对于本题,dfs 中同时 update 与 merge,那么就需要将 merge 可持久化。
这种写法好处是绝对不会错,劣处是空间加大,一般会多个常数。所以能不可持久化就别可持久化。
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=3e5+6;
const int M=6e6+7;
const int lim=1e9;
int n,m,dep[N],sz[N],tr[M],ls[M],rs[M],rt[N],head[N],id,tot=1;
struct edge{
int to,nxt;
}e[N<<1];
inline void addedge(int u,int v){
e[++tot].to=v;
e[tot].nxt=head[u];
head[u]=tot;
return;
}
inline void pushup(int p){
tr[p]=tr[ls[p]]+tr[rs[p]];
return;
}
inline void update(int &p,int l,int r,int now,int val){
if(!p)p=++id;
if(l==r){
tr[p]+=val;
return;
}
int mid=(l+r)>>1;
if(now<=mid)update(ls[p],l,mid,now,val);
else update(rs[p],mid+1,r,now,val);
pushup(p);
return;
}
inline int merge(int x,int y){
if(!x||!y)return x|y;
int p=++id;
tr[p]=tr[x]+tr[y];
ls[p]=merge(ls[x],ls[y]),rs[p]=merge(rs[x],rs[y]);
return p;
}
inline int query(int p,int l,int r,int s,int t){
if(s<=l&&r<=t)return tr[p];
int mid=(l+r)>>1,res=0;
if(s<=mid)res+=query(ls[p],l,mid,s,t);
if(t>mid)res+=query(rs[p],mid+1,r,s,t);
return res;
}
inline void dfs(int u,int fa){
dep[u]=dep[fa]+1;
sz[u]=1;
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(v==fa)continue;
dfs(v,u);
sz[u]+=sz[v];
rt[u]=merge(rt[u],rt[v]);
}
update(rt[u],1,n,dep[u],sz[u]-1);
return;
}
signed main(){
scanf("%lld%lld",&n,&m);
for(int i=1;i<n;i++){
int u,v;
scanf("%lld%lld",&u,&v);
addedge(u,v);
addedge(v,u);
}
dfs(1,0);
while(m--){
int u,k,ans;
scanf("%lld%lld",&u,&k);
printf("%lld\n",min(k,dep[u]-1)*(sz[u]-1)+query(rt[u],1,n,dep[u]+1,min(n,dep[u]+k)));
}
return 0;
}
习题
模板题。
交换左右子树对当前节点和前面的所有节点没有影响,所以产生逆序对当且仅当 \(u,v\) 在左右子树中。
那么在合并线段树的过程中统计交换子树的逆序对个数和不交换子树的逆序对个数取 min。
逆序对个数显然就是左子树大小乘上右子树大小。
一个节点 \(u\) 的 \(k\) 级 cousin 个数相当于 \(u\) 的 \(k\) 辈父亲 \(fa\) 的 \(k\) 级儿子个数减一(减去 \(u\))。
先将询问离线,然后倍增得到每个点的 \(k\) 辈父亲。
对于每个节点 \(fa\),查询 \(fa\) 字数内有多少节点 \(u\) 满足 \(dep_{fa}+k=dep_i\)
那么给每个点建立权值线段树后合并。
二. 线段树合并与其他结合
对于每一个节点开一棵线段树维护其重要度。
那么一开始对于每个节点都是一棵树,当 \(x\) 到 \(y\) 加入一条边的时候,将它们的线段树合并。同时使用并查集合并两个点,这样可以处理出对于每一个点,其所在的连通块。
查询点 \(u\) 所在的连通块的根的权值线段树,在权值线段树上找到第 \(k\) 小。这个不熟悉可以去看权值线段树部分。
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+6;
const int M=4e6+7;
int tr[M],ls[M],rs[M],id[M],n,m,Q,fa[N],rt[N],lim,tot;
inline void pushup(int p){
tr[p]=tr[ls[p]]+tr[rs[p]];
return;
}
inline void update(int &p,int l,int r,int now,int idx){
if(!p)p=++tot;
if(l==r){
tr[p]++;
id[p]=idx;
return;
}
int mid=(l+r)>>1;
if(now<=mid)update(ls[p],l,mid,now,idx);
else update(rs[p],mid+1,r,now,idx);
pushup(p);
return;
}
inline int merge(int x,int y,int l,int r){
// cout<<x<<" "<<y<<" "<<l<<" "<<r<<"&\n";
if(!x||!y)return x|y;
if(l==r){
if(!id[x])id[x]=id[y];
tr[x]+=tr[y];
return x;
}
int mid=(l+r)>>1;
ls[x]=merge(ls[x],ls[y],l,mid);
rs[x]=merge(rs[x],rs[y],mid+1,r);
pushup(x);
return x;
}
inline int query(int p,int l,int r,int k){
// cout<<p<<" "<<l<<" "<<r<<" "<<k<<" "<<tr[p]<<"*\n";
if(!p||tr[p]<k)return -1;
if(l==r)return id[p];
int mid=(l+r)>>1;
if(tr[ls[p]]>=k)return query(ls[p],l,mid,k);
else return query(rs[p],mid+1,r,k-tr[ls[p]]);
}
inline int find(int x){
if(fa[x]==x)return x;
return fa[x]=find(fa[x]);
}
inline void addedge(int u,int v){
u=find(u),v=find(v);
if(u==v)return;
fa[v]=u;
rt[u]=merge(rt[u],rt[v],1,lim);
return;
}
int main(){
scanf("%d%d",&n,&m),lim=n;
for(int i=1;i<=n;i++){
int x;
fa[i]=i;
scanf("%d",&x);
update(rt[i],1,lim,x,i);
}
for(int i=1;i<=m;i++){
int u,v;
scanf("%d%d",&u,&v);
addedge(u,v);
}
scanf("%d",&Q);
while(Q--){
int u,v,k;
char op;
// scanf("%c",&op);
cin>>op;
if(op=='Q'){
scanf("%d%d",&u,&k);
printf("%d\n",query(rt[find(u)],1,lim,k));
}
else{
scanf("%d%d",&u,&v);
addedge(u,v);
}
}
return 0;
}
习题
考虑将查询离线下来,然后按照 \(x\) 从小到大排序。对于加边也是同理,按照边权从小到大排序。
处理询问时,从边中找到边权小于 \(x\) 的并加入。这部分由于询问与边权均单调递增,故时间复杂度为 \(O(n)\)。
那么查询点 \(u\) 所在的连通块中就没有边权大于 \(x\) 的点了。那么这就与永无乡一模一样了。
标签:return,int,tr,线段,合并,笔记,merge,ls From: https://www.cnblogs.com/trsins/p/17970746