这个hack数据是真的强。
模板题的题解很重要哦,希望你能找到适合自己的。
李超线段树的定义
对于李超线段树的定义,JHSeng大佬的定义简洁精炼:
李超线段树是一种用于维护平面直角坐标系内线段关系的数据结构。
而洛谷P4097Segment就是李超线段树维护的板子题了。
题目大意(偷个懒):
要求在平面直角坐标系下维护两个操作:
1. 在平面上加入一条线段。记第 $i$ 条被插入的线段的标号为 $i$。
2. 给定一个数 $k$,询问与直线 $x = k$ 相交的线段中,交点纵坐标最大的线段的编号。
具体维护操作
我们主要维护区间内最优线段。
我们假设平面内已有一条线段:

这时显然,其为所有区间内的最优线段,接下来我们再插入一条线段。
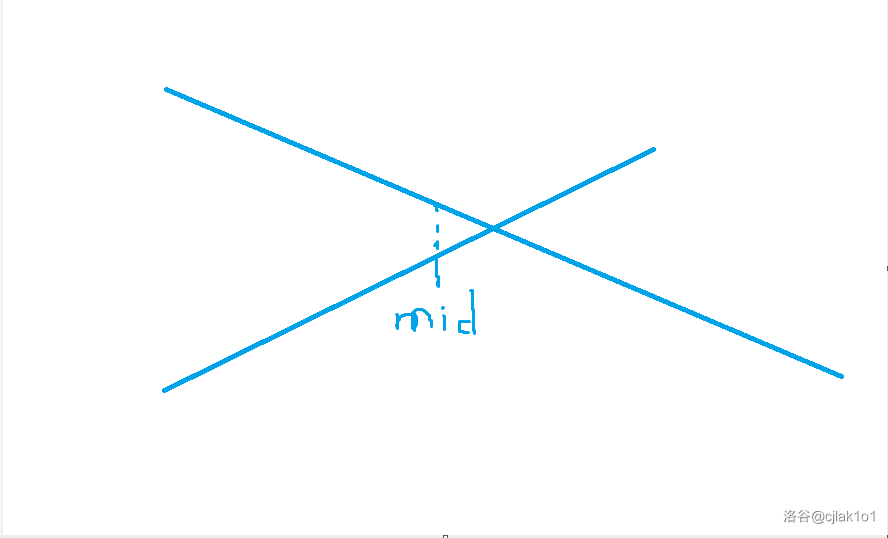
明显可以看出,插入新的线段后,两条线段的交点左区间最优线段为新线段,而交点右边区间最优线段则为原来的线段。扫一遍肯定来不及,所以我们二分递归求出所有区间的最优线段。
首先先取当前处理区间的 \(mid\),如果新线段在 \(x=mid\) 时纵坐标更大,则先将当前区间的最优线段更替为新线段,从这里可以看出,每一个区间长度大于一的区间存的线段,只满足取区间内大部分横坐标其为最优解。
if(f[i](mid)-f[id](mid)>eps) swap(i,id);
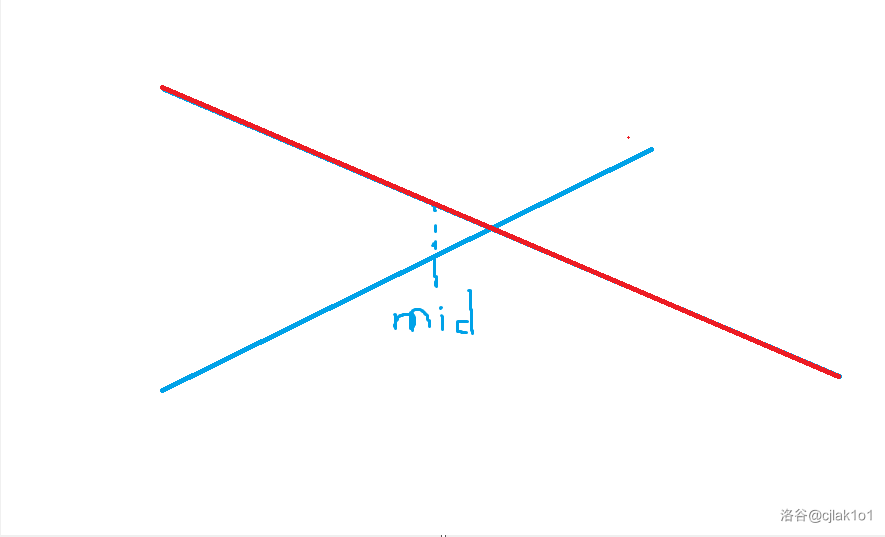
红色线段为最优线段。
但是实际上交点右边的区间最优线段不是它,所以我们要两条线段再次进行比较,比较区间的左右两端点(即是判断区间内两条线段是否有交点,有交点说明要重新更新)。
如果被淘汰的线段在左右端点的比较中胜出,则将它继续递归,更新。
if(f[i](l)-f[id](l)>eps||(f[i](l)==f[id](l)&&i<id)) upd(lson,ql,qr,i);
if(f[i](r)-f[id](r)>eps||(f[i](r)==f[id](r)&&i<id)) upd(rson,ql,qr,i);
最后得出所有区间的最优线段。
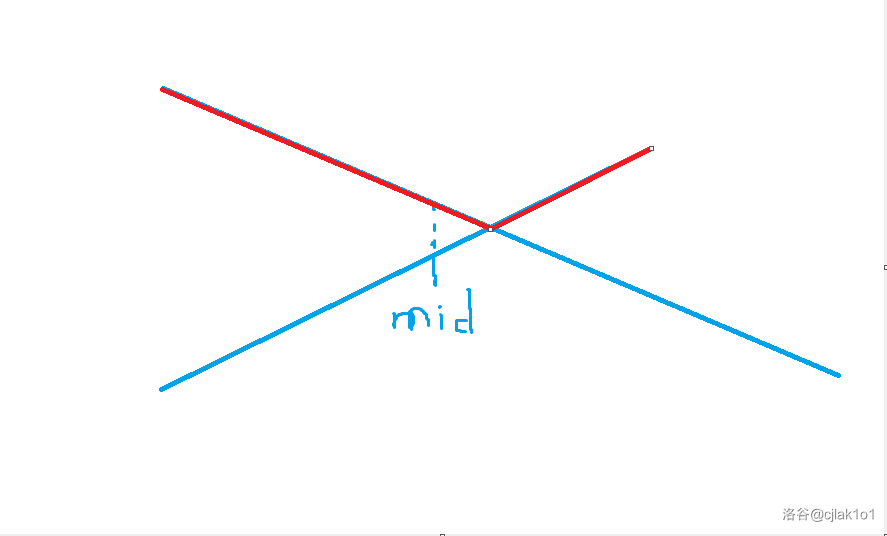
询问的时候单点询问,递归取 max 即可。
一个蒟蒻入坑过的小问题
蒟蒻在第一次写李超线段树的时候,非常不明白询问的时候为什么要取 max。单点询问直接取当前点的最优线段不久行了,在经过思考后,发现:
-
李超线段树没有或者说不需要 push_down 操作,所以可能当前点并没有值。
-
李超线段树大区间和小区间内存的都不一定是最优线段,大区间刚刚讲过了,只是满足大部分,而小区间由于没有 push_down 也可能出现存的不是最优解,例如如图所示的情况。
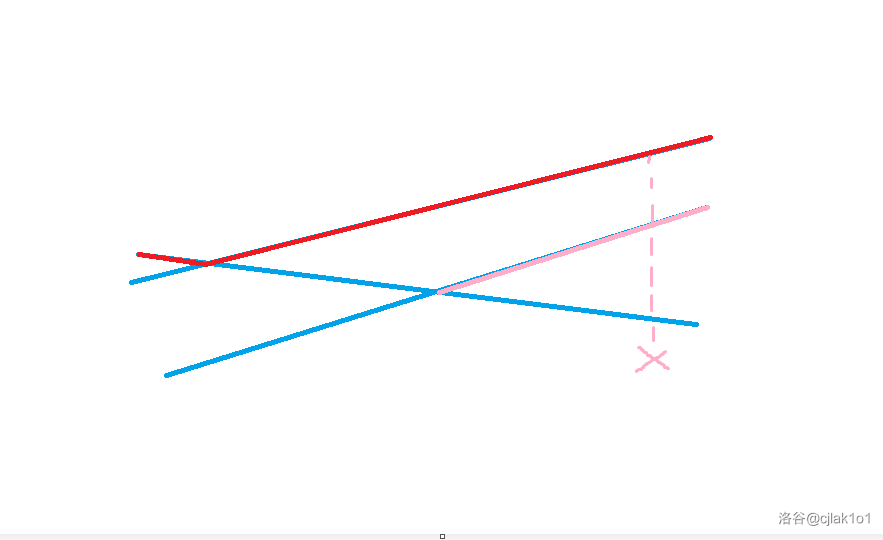
当前询问 \(x\) 点的最高纵坐标,假如第二条直线时,一二条直线右边区间的最优线段变为了图中粉色区间,而再加入第三条线段时,更新最优线段后,由于被淘汰的线段在中间和右边都比不过新线段,所以图示粉色区间并没有被递归更新,造成了小区间非最优解的情况。