前置芝士:最小生成树、Kruskal 算法、瓶颈(图上路径最值)
正文
定义
在执行 Kruskal 算法的过程中我们会从小到大加入若干条边,现在我们仍然按照这个顺序。
首先新建 \(n\) 个集合,每个集合恰有一个节点,点权为 \(0\)。
每一次加边会合并两个集合,我们可以新建一个点,点权为加入边的边权,同时将两个集合的根节点分别设为新建点的左儿子和右儿子。
然后我们将两个集合和新建点合并成一个集合,将新建点设为根。
不难发现,在进行 \(n-1\) 轮之后我们得到了一棵恰有 \(n\) 个叶子的二叉树,同时每个非叶子节点恰好有两个儿子。
这棵树就叫 Kruskal 重构树。
举个栗子:
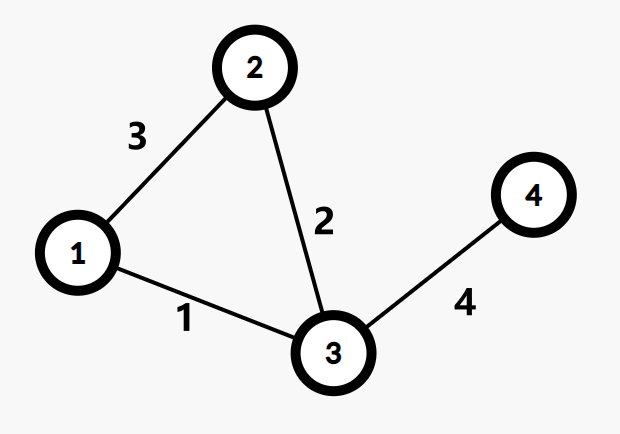
(图源自 OI Wiki)
这张图的 Kruskal 重构树如下:
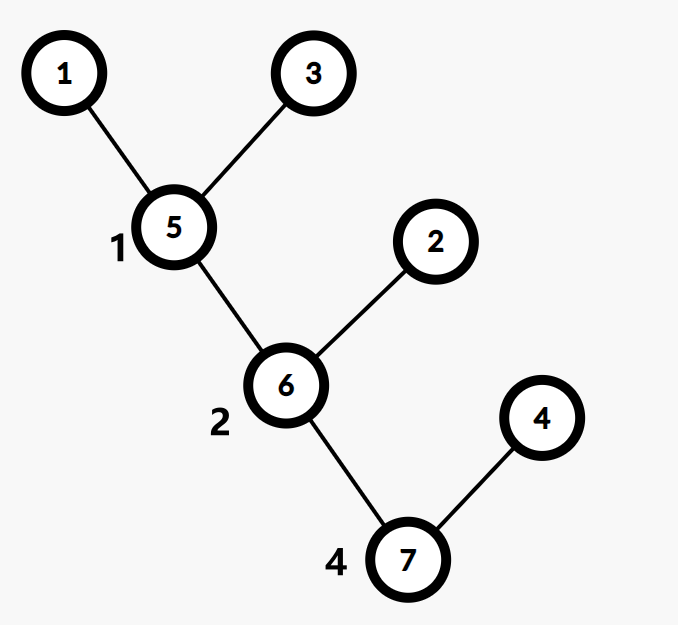
(图源自 OI Wiki)
性质
不难发现,原图中两个点之间的所有简单路径上最大边权的最小值 与 最小生成树上两个点之间的简单路径上的最大值 等于 Kruskal 重构树上两点之间的 LCA 的权值。
也就是说,到点 \(x\) 的简单路径上最大边权的最小值小于等于 \(val\) 的所有点 \(y\) 均在 Kruskal 重构树上的某一棵子树内,且恰好为该子树的所有叶子节点。
我们在 Kruskal 重构树上找到 \(x\) 到根的路径上权值小于等于 \(val\) 的最浅的节点。显然这就是所有满足条件的节点所在的子树的根节点。
如果需要求原图中两个点之间的所有简单路径上最小边权的最大值,则在跑 Kruskal 的过程中按边权大到小的顺序加边。
END.
标签:重构,Kruskal,路径,笔记,集合,节点,边权 From: https://www.cnblogs.com/cantorsort2919/p/16599227.html