标签：直线 题解 LL Hard T403510 平面 2n

Link

T403510 平面划分(Hard)

Question

平面上由 \(n\) 条这样的折线所界定区域的最大的个数 \(Z_n\) 是多少。

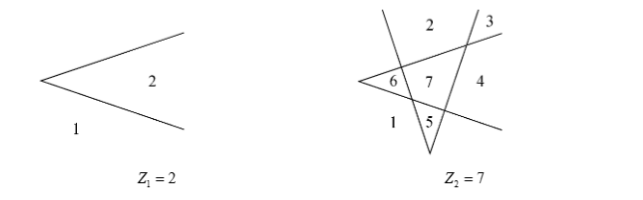
Solution

先思考一个简单的问题

平面上 \(n\) 条直线所界定的区域最大个数 \(L_n\) 是多少？

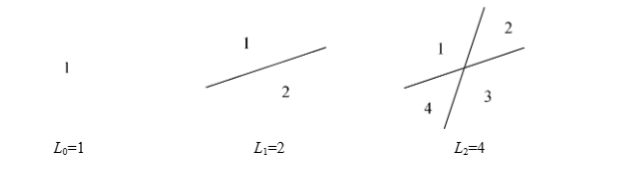
我们考虑假设已经有\(n-1\) 条直线，我们需要画一条直线，这条直线最多和 \(n-1\) 条直线相交产生 \(n\) 个新的区域

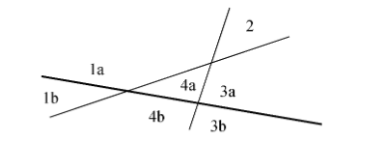
所以我们得到了

\[\begin{align*} &L_0=1 \\ &L_n=L_{n-1}+n (n >0) \end{align*}\]

很容易我们可以得出 \(L_n=\frac{n(n+1)}{2}+1,n \ge0\)

然后再来思考原问题

考虑一个折线可以看作两条直线擦掉一半，对于每个折线，我们都失去了 \(2\) 块区域

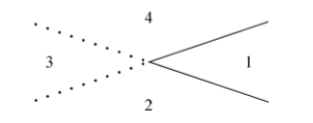
所以

\[\begin{aligned} Z_n & = L_{2n}-2n \\ & = \frac{2n(2n+1)}{2}+1-2n\\ & = 2n^2-n+1,n \ge 0 \end{aligned}\]

Code

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const LL TT=1e9+7;
int main() {
    LL N;
    cin>>N;
    cout<<(2*N*N-N+1)%TT<<endl;
    return 0;
}

标签：直线,题解,LL,Hard,T403510,平面,2n
From： https://www.cnblogs.com/martian148/p/17882101.html