DP2
UVA12141 Line Chart
先离散化一波,记位置从小到大第 \(i\) 个元素离散化后的大小为 \(a_i\)。
这题最大的难点就在于如何避免计重。
如果现在要更新 \(i\) 位置的 dp 值,且 \(\exists p < q, a_p = a_q \neq a_i\),则贪心地考虑用 \(q\) 转移,而不是 \(p\),因为 \(q\) 位置结尾包含了以 \(p\) 位置结尾的所有情况。
记 \(f_{x, w, 0 / 1}\) 表示以 \(x\) 结尾,峰数为 \(w\),当前为下降/上升的方案数,并记 \(g_{x}\) 表示以 \(x\) 开头的方案数(\(0 \text{ or } 1\))。当出现一个 \(x\) 与之前相同时,拿当前位置的新 dp 值覆盖之前的 dp 值。
\[\begin{aligned} f_{x, w, 0} &\leftarrow \sum\limits_{i = x + 1}^{n}f_{i, w, 0} + g_{i}[w = 0] \\ f_{x, w, 1} &\leftarrow \sum\limits_{i = 1}^{x - 1}f_{i, w, 1} + g_{i}[w = 0] \\ f_{x, w + 1, 0} &\leftarrow \sum\limits_{i = x + 1}^{n}f_{i, w, 1} \\ f_{x, w + 1, 1} &\leftarrow \sum\limits_{i = 1}^{x - 1}f_{i, w, 0} \\ g_{x} &|= 1 \end{aligned} \]可以拿树状数组优化,时间复杂度为 \(O(nk\log{n})\)。
warning:注意要从大到小枚举 \(w\)。不要在 \(w\) 把 \(w + 1\) 时刚更新的 dp 值给覆盖了, ,,
P8863 「KDOI-03」构造数组
首先可以把 \(n = 1\) 和 \(\sum\limits_{i = 1}^{n}b_i \equiv 1\pmod{2}\) 的无解特判了。
记 \(m = \frac{\sum\limits_{i = 1}^{n}b_i}{2}\),原问题可以看作是用指定数量的 \(1, 2, \dots, n\) 构造出 \(m\) 个二元组。
拆开 考虑二元组,即对于一个二元组,先填第一个数 \(x\),再填第二个数 \(y\)(钦定 \(x < y\))。
从小到大填数,需要满足相同的数不能填进同一个二元组,且不能填进已经完整的二元组。
这个过程不会使之前不同的填法最终导致相同的结果,也就是不会计重。
然后就方便我们设计 dp 状态了:
设 \(f_{i, j, k}\) 表示考虑前 \(i\) 个数(\(1 \sim i\)),空二元组数量为 \(j\),已填一个数的二元组数量为 \(k\) 的方案数。枚举将几个 \(i\) 去填空二元组:
\[\begin{aligned} f_{i, j - x, k + 2x - b_i} \leftarrow \binom{j}{x}\binom{k}{b_i - x}f_{i - 1, j, k} \end{aligned} \]我趣,\(O(nm^3)\),裂开来。
不要急,用一个经典套路,由于 \(w = \sum\limits_{c = 1}^{i - 1}b_c\) 是确定的,因此只要确定了 \(j\),就能直接定下 \(k = 2m - 2j - w\)。
重新设 \(f_{i, j}\) 表示考虑前 \(i\) 个数(\(1 \sim i\)),空二元组数量为 \(j\) 的方案数。
\[\begin{aligned} f_{i, j - x} \leftarrow \binom{j}{x}\binom{2m - 2j - w}{b_i - x}f_{i - 1, j} \end{aligned} \]我趣,\(O(nm^2)\),裂开来。
等一等,真的如此吗?注意到每次枚举的 \(x\) 的范围上界是 \(b_i\),而 \(\sum\limits_{i = 1}^{n}b_i = 2m\),因此时间复杂度应该为 \(O(m^2)\)!
膜拜 \(\color{black}{\text{l}}\color{red}{\text{iuhangxin}}\) 教会我分析时间复杂度。
P3354 [IOI2005] Riv 河流
一看到这个分段求最小值就触动 DNA 了!WQS 二分!
先放一放,因为此题的数据范围没必要上这么高级的东西,重点是如何学会 DP。如何学会 DP!如何学会 DP?如何学会 DP!如何学会 DP!如何学会 DP?如何学会 DP!如何学会 DP!如何学会 DP!如何学会 DP?如何学会 DP?如何学会 DP!如何学会 DP!如何学会 DP!如何学会 DP!
记 \(f_{u, x, i}\) 表示考虑以 \(u\) 为节点的子树,\(u\) 下游最近的伐木场为 \(x\),\(u\) 子树内共选了 \(i\) 个伐木场的最小花费。
从子节点 \(v\) 转移至 \(u\)。
\[\begin{aligned} f_{u, x, i + j} \xleftarrow{\min} f_{u, x, i} + \min(f_{v, x, j}, f_{v, v, j}) \\ \end{aligned} \]最后进行转移 \(f_{u, x, i} \leftarrow w_u \times (d_{u} - d_{x})\),其中 \(d_u\) 表示 \(u\) 到根的距离。若 \(u = x\),还需将第三维整体平移一个单位。
最后答案为 \(f_{0, 0, K + 1}\)。注意根节点本身就有一个伐木场。
范围这么小的 dp 要大胆一点!缺什么信息就设什么信息!
之后补一下 WQS 二分的做法。
2023.09.27T2
Problem
给定 \(n\) 个区间和一个正整数 \(K\),你要将 \(n\) 个区间分成 \(K\) 组,使得每组线段的交不为空。
求出合法分组方案中每组线段交长度之和的最大值。
\(n, K \le 8000\)。
Solution
想到大概可以钦定一个区间的顺序,然后进行一个 \(O(n^3)\) 的 DP 转移。然而我连这个都不会!很差劲!
然而到达 \(O(n^3)\) 的过程也确实有点神仙。
首先要指出一个显然的性质:当线段 \(L\) 包含至少一条线段时,线段 \(L\) 的贡献只有两种大类——与被包含的线段一组,相当于 \(L\) 没有贡献;\(L\) 自成一组,贡献 \(L\) 自身的长度。
所以可以 去掉包含关系:将包含至少一条线段的线段拎出来,组成集合 \(S\),把其余的线段记为 \(T\)。枚举 \(S\) 中有 \(w\) 个线段自成一组,贪心地选取长度最大的 \(w\) 个进行贡献,\(S\) 中的其余线段可以忽略;然后将 \(T\) 中的线段分成 \(K - w\) 组,而 \(T\) 中的线段之间没有包含关系,所以可以直接对 \(T\) 从前往右做一个 DP!这正是我想要的!
回味一下,这正体现了 拆贡献 的思想!为什么又又又又没有想到呢?
具体地,记 \(f_{i, j}\) 表示 \(T\) 中的前 \(i\) 条线段(已从前往后排序),分成了 \(j\) 组的最大价值。
\[\begin{aligned} f_{i, j} = \max\limits_{j - 1 \le k \le i - 1, r_{k + 1} > l_i}(f_{k, j - 1} + r_{k + 1} - l_{i}) \end{aligned} \]这样能做到 \(O(n^3)\)。
考虑优化。当 \(i\) 单增时,\(k\) 的合法区间也是单增的,而我们想快速得到所有合法 \(k\) 中 \(f_{k, j - 1} + r_{k + 1}\) 的最大值。想到了什么!那就对每一个 \(j\) 都维护一个单调队列,即可 \(O(1)\) 得到 \(f_{k, j - 1} + r_{k + 1}\) 的最大值了!
于是就可以 \(O(n^2)\) 了。注意单调队列中各个操作的先后顺序!
P4362 [NOI2002] 贪吃的九头龙
当 \(K + M - 1 > N\) 时,无解。以下认为 \(K, M, N\) 同阶。
记 \(f_{u, c, i}\) 表示考虑 \(u\) 子树内,\(u\) 节点颜色为 \(c\),共选了 \(i\) 个大头的最小 “难受值”。转移是简单的树形背包。问题是如何保证每组颜色都至少对应一个节点?这实际上是一个令人迷惑的信息——我们进行 dp 试图使得边的代价和尽量小,则最优情况下一定会考虑用完所有颜色!所以大胆做就可以了。
\[\begin{aligned} f_{u, c, i + j} \xleftarrow{\min} f_{u, c, i} + f_{v, c, j} + w(u, v) \\ f_{u, c, i + j} \xleftarrow{\min} f_{u, c, i} + \min\limits_{d \neq c}(f_{v, d, j}) \end{aligned} \]其中 \(\min\limits_{d\neq c}(f_{v, d, j})\) 可以在对 \(v\) 处理完后拎出来前后缀最小值预处理,因此总时间复杂度可以做到 \(O(N^3)\)。
然而 \(O(N^3)\) 很劣!甚至还要用 vector 卡空间。
事实上,\(2 \sim M\) 的颜色可以看成一类,\(1\) 单独看成一类。对于 \(2 \sim M\) 颜色节点间的连边,一定贪心地让两个端点颜色不同,因为不用考虑 \(2 \sim M\) 颜色的节点数量(保证每种颜色至少对应一个节点显然可以调整使得条件满足)。然后就可以把第二维优化成 \(O(1)\) 的了!
转移分为 \(1 \to 1, 1 \to 2\sim M, 2 \sim M \to 2\sim M\) 三类。
注意这样优化后,要对 \(M = 2\) 的转移单独判一下,因为 \(2 \sim M \to 2 \sim M\) 的转移只能是 \(2 \to 2\) 的连边了。
P5299 [PKUWC2018] Slay the Spire
洛谷:P5299 [PKUWC2018] Slay the Spire
LOJ:#2538. 「PKUWC2018」Slay the Spire
前言:请分清楚 使用 和 抽取。九条要 抽取 \(m\) 张牌,但只会 使用 \(k\) 张牌。
首先考虑当抽出的 \(m\) 张牌确定时的策略:记 \(m\) 张牌中强化牌的数量为 \(c\)。
贪心策略是:使用强化牌至少使伤害翻一倍,一定不劣于使用一张攻击牌。
- 若 \(c < k - 1\):强化牌全部使用,并优先使用,再使用 \(k - c\) 张数值较大的攻击牌。
- 若 \(c \ge k - 1\):先使用 \(k - 1\) 张数值较大的强化牌,再使用 \(1\) 张数值最大的攻击牌。
也就是说,在最优策略下,九条使用的强化牌一定是数值前 \(w_1\) 大的,使用的攻击牌一定是前 \(w_2\) 大的。
对攻击牌和强化牌按数值从大到小排序后分别进行 DP,再组合起来计数。由于还要考虑到有些牌被抽取但并未被使用,因此我们想要的 DP 状态中应该包含 “使用到了哪张牌” 的信息。如果最终使用到了第 \(x\) 张牌,则 \(x\) 之前的未被选择的牌也一定未被抽取;而 \(x\) 之后的的牌的抽取情况,可以通过组合数算出。
具体地,记 \(f_{i, j}\) 表示考虑前 \(i\) 张强化牌,第 \(i\) 张必使用,共使用 \(j\) 张牌的数值乘积之和;记 \(g_{i, j}\) 表示考虑前 \(i\) 张攻击牌,第 \(i\) 张必使用,共使用 \(j\) 张牌的数值和之和。
直接做不方便转移,于是我又记 \(f^{'}_{i, j}\) 表示考虑前 \(i\) 张强化牌,共使用 \(j\) 张牌的数值乘积之和; \(g^{'}_{i, j}\) 表示考虑前 \(i\) 张攻击牌,共使用 \(j\) 张牌的数值和之和。
转移是容易的:
\[\begin{aligned} f^{'}_{i, j} &\leftarrow f^{'}_{i - 1, j} \\ f^{'}_{i, j + 1} &\leftarrow f^{'}_{i - 1, j} \times a_i \\ f_{i, j + 1} &\leftarrow f^{'}_{i - 1, j} \times a_i \\ \\ g^{'}_{i, j} &\leftarrow g^{'}_{i - 1, j} \\ g^{'}_{i, j + 1} &\leftarrow g^{'}_{i - 1, j} + \binom{i - 1}{j}\times b_i \\ g_{i, j + 1} &\leftarrow g^{'}_{i - 1, j} + \binom{i - 1}{j}\times b_i \\ \end{aligned} \]注意 \(g\) 的转移时要给之前的每一个选取方案都加上一个 \(b_i\)。
对 \(c < k - 1\) 和 \(c \ge k - 1\) 分别计数:
-
\(c < k - 1\) 时:被抽取但未被使用的牌一定是攻击牌。
\[\begin{aligned} ans \leftarrow f_{i, j} \times g_{x, k - j} \times \binom{n - x}{m - k} \end{aligned} \]其中 \(i\) 可以对每个 \(j\) 预求和优化掉。
-
\(c \ge k - 1\) 时:被抽取但未被使用的牌既可能是攻击牌,也可能是强化牌。
\[\begin{aligned} ans \leftarrow f_{i, k - 1} \times g_{x, 1} \times \binom{(n - i) + (n - x)}{m - k} \end{aligned} \]
时间复杂度为 \(O(n^2)\)。这里认为 \(k, n, m\) 同阶。
实现上,最好 \(O(n^2)\) 预处理组合数,不要用阶乘及其逆元当场算,否则会因取模过多而卡 TLE。
P8162 [JOI 2022 Final] 让我们赢得选举 (Let's Win the Election)
只有三种情况:选 \(A\),选 \(B\),不选。并且确定了所选的 \(A, B\) 后,一定先处理 \(B\),再处理 \(A\)。对于所选的 \(B\),一定先处理小的,再处理大的。
将所有二元组按 \(B\) 从小到大排序。
这时需要发现一个重要的贪心策略:如果所选的 \(B_i\) 之前有一个没有选的 \(B_j\),则去选 \(B_j\) 而不选 \(B_i\) 一定不劣。
进一步,二元组可以分成前后两个部分:前面部分,只能选 \(A\) 或选 \(B\);后面部分,只能选 \(A\) 或不选。
对前面部分,记 \(f_{i, j, k}\) 表示考虑前 \(i\) 个位置,最终要选 \(j\) 个 \(B\),已经选了 \(k\) 个 \(B\) 的最小代价。
当状态 \(f_{i, j, k}\) 中 \(j = k\) 时,后面部分一定选最小的 \(K - i\) 个 \(B\)。总时间复杂度 \(O(n^3)\)。
P6235 [eJOI2019] 矩形染色
对 \(a\) 序列代表的斜线用 \(x - y\) 编号,对 \(b\) 序列代表的斜线用 \(x + y\) 编号,奇偶性不同的斜线的选取相互独立,所以我们可以只考虑其中一种情况,另一种情况类似处理。
每个 \(a\) 中的元素都对应了 \(b\) 中的一段区间,即如果 \(b\) 中的某一段区间都被选择,则对应 \(a\) 中的某些元素可以不被选择。预处理出每个能够消除 \(a\) 中某元素的极小区间,区间数量显然是 \(O(n)\) 的。
然后转成了经典问题 Codeforces:CF115E Linear Kingdom Races,用线段树维护一下即可。
P5999 [CEOI2016] kangaroo
以下几题均为 连续段 DP 的技巧。这里有一篇还不错的笔记。我个人习惯将这种类型的 DP 称作 插空 DP。实际上在之前遇到过很多按 排名 DP 的题,本质思想就是将元素进行插空进行 DP。插空 DP 的转移比较简单,难点在于如何把原问题和 DP 的状态设计联系起来,这通常需要对原问题进行转化或数学模型的可视化。
该题就是一个极其生动的抽象的例子。
朴素的 DP 设计是:\(f_{i, j, k, 0 / 1}\) 表示考虑已经遍历了 \(i\) 个地点,起点为 \(j\), 终点为 \(k\),最后一步跳跃的方向为 \(0 / 1\) 的的方案数。\(O(n^4)\)。貌似有人硬把它优化成 \(O(n^3)\) 带上巨小的常数过了,恐怖如斯。
然后是主题 —— \(O(n^2)\) 的插空法 DP。
原问题等价于:询问有多少个 \(n\) 元排列,使得 \(p_1 = s, p_n = t\),且 \(\forall i \in [2, n - 1]\),\(p_i > p_{i - 1} \and p_i > p_{i + 1}\) 或 \(p_i < p_{i - 1} \and p_i < p_{i + 1}\)。
考虑从小到大插入元素(或者考虑将排列视作折线图,从下往上扫描)对连续段的影响。设 \(f_{i, j}\) 表示考虑数 \(1 \sim i\),形成了 \(j\) 个连续段的方案数。
- 新建一个连续段:\(f_{i, j} \leftarrow f_{i - 1, j - 1}\times j\)。
- 合并两个连续段:\(f_{i, j} \leftarrow f_{i - 1, j + 1} \times j\)。
注意由于两侧相邻元素与中间元素大小关系一致的性质,故不可能出现在一个连续段中新增元素的情况。
另外,如果 \(p_1, p_n\) 已经确定,则新建一个连续段的转移系数要减去左右两侧的空位。
对于 \(s, t\) 的插入,特殊处理一下即可。
听说还有线性做法,恐怖如斯。
P7967 [COCI2021-2022#2] Magneti
如果确定了磁铁的放置顺序,则可以知道使磁铁不会相互吸引所需占据的最小空位数 \(x\)。假设使得占据的最小空位数为 \(x\) 的放置方案数有 \(f_{x}\) 种,则答案为:
\[\begin{aligned} ans &= \sum\limits_{i = 1}^{l}f_{i} \times \binom{l - i + n}{n} \end{aligned} \]求 \(f\) 用到插空法 DP。下面这一步也很巧妙:考虑将磁铁按影响范围从小到大插入,这样每次对占据区域大小的影响可以轻松确定。记 \(f_{i, j, x}\) 表示考虑前 \(i\) 个磁铁,形成 \(j\) 个连续段,占据的最小空位数为 \(x\) 的方案数。为了方便表示,记 \(a_i = r_i - 1\)。
- 新建一个连续段:\(f_{i, j, x + 1} \leftarrow f_{i - 1, j - 1, x} \times j\)。
- 在一个连续段中加入当前磁铁:\(f_{i, j, x + a_i + 1} \leftarrow f_{i - 1, j, x}\times j \times 2\)。
- 合并两个连续段:\(f_{i, j, x + 2a_i + 1} \leftarrow f_{i - 1, j + 1, x} \times j\)。
第一维用滚动数组优化一下。时间复杂度 \(O(n^2l)\)。
P9197 [JOI Open 2016] 摩天大楼
终于来到了这道典中典!有了前两题的经验,我们能想到将整数按一定顺序插入进行 DP;如有必要,还可以将数列视作一个折线图,将 DP 过程形象成一根扫描线的移动。那么直观的折线图对解决此题是很有帮助的,这相当于问你所有排列的情况中,相邻两个高度的差的绝对值。
然后由于洛谷题解讲得太好了所以就直接搬图了。
考虑从上往下扫描折线图:
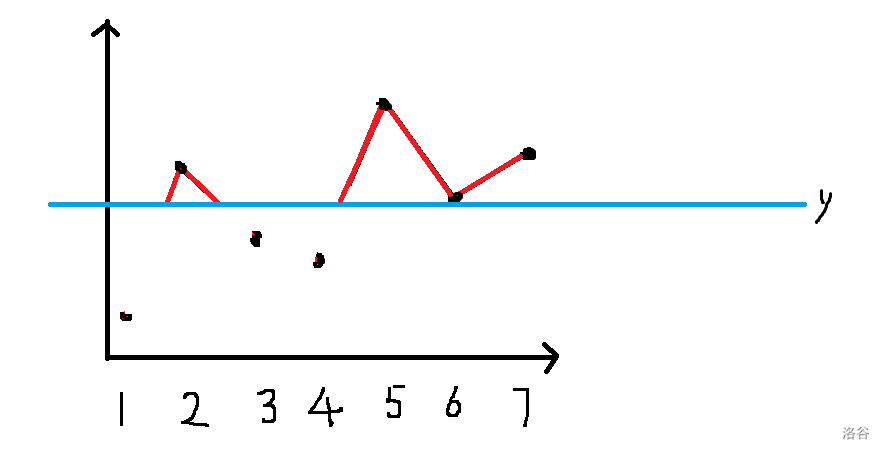
每从一个位置移动到下一个点加入时,都会产生若干段等长的线段累计入答案,而贡献线段的数量与连续段的数量以及是否选取最左侧点与最右侧点有关。可以说,此题与 P5999 [CEOI2016] kangaroo 非常相似。
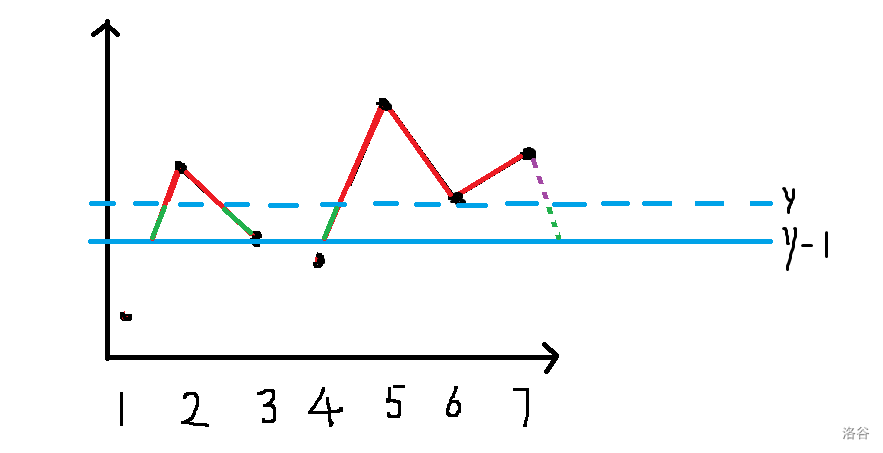
记 \(f_{i, j, w, 0 / 1, 0 / 1}\) 表示考虑前 \(i\) 大的元素,共形成 \(j\) 个连通块,高度差值累计为 \(w\),且最左 / 右侧位置是否被填的方案数。
实际上可以把后两维合起来,表示左右端点共填了 \(0 / 1/ 2\) 个,效率更高。
转移是简单的 dirty work,在此不赘述。
P6189 [NOI Online #1 入门组] 跑步
这也是个经典的 DP 模型啊!第一次见到这个模型是在 这个题,记得有一篇题解形象地将其称为 柱状图 DP,其主要思想是 通过插入元素与整体加值实现根号复杂度构造数列,本质是 对背包的优化。
考虑根号分治,记 \(m = \sqrt{n}\),对 \(< m\) 的元素和 \(\ge m\) 的元素分别考虑贡献。
-
对于 \(< m\) 的元素,直接上完全背包。由于物品数为 \(O(m)\),背包体积为 \(O(n)\),所以时间复杂度为 \(O(nm) = O(n\sqrt{n})\)。
-
对于 \(\ge m\) 的元素,考虑柱状图 DP。具体地,记 \(f_{i, j}\) 表示使用 \(i\) 个 \(\ge m\) 元素,和为 \(j\) 的方案数。
- \(f_{i, j} \leftarrow f_{i - 1, j - m}\):加入一个元素 \(m\)。
- \(f_{i, j} \leftarrow f_{i, j - i}\):将当前的 \(i\) 个元素集体加一。
由于第一维物品的数量是 \(O(\sqrt{n})\) 的,背包体积为 \(O(n)\),所以时间复杂度为 \(O(n\sqrt{n})\)。
枚举两部分的贡献分配和 \(\ge m\) 选取的元素个数。总时间复杂度为 \(O(n\sqrt{n})\)。
P8340 [AHOI2022] 山河重整
[BJOI2019] 排兵布阵
一眼背包,显然有用的物品数只有 \(O(ns)\) 个,直接做 \(O(snm)\) 的背包 DP 即可。
P5323 [BJOI2019] 光线
题目所求的物理量叫做透光率。
采用整体 / 替换思想,把前 \(i\) 张玻璃等效成一张玻璃,我们通过维护这张等效玻璃的反射率和透光率进行递推求解。
记 \(f_{i}, g_{i}\) 分别表示前 \(i\) 张玻璃的等效玻璃的透光率 / 反射率,则:
\[\begin{aligned} f_{i} &= f_{i - 1}(a_{i} + b_{i}\times g_{i - 1}\times a_{i} + (b_{i}\times g_{i - 1})^{2}\times a_{i} + \dots) = f_{i - 1}\times a_{i}\times \frac{1}{1 - b_{i}\times g_{i - 1}} \\ g_{i} &= b_{i} + a_{i}\times g_{i - 1}\times a_{i} + a_{i}\times g_{i - 1}\times b_{i}\times g_{i - 1}\times a_{i} + \dots = b_{i} + a_{i}^{2}\times g_{i - 1}\times \frac{1}{1 - b_{i}\times g_{i - 1}} \\ \end{aligned} \]