title: LoRA 笔记
banner_img: https://proxy.thisis.plus/202305091237913.png
date: 2023-6-13 0:12:40
tags:
- 文字生成图片
LoRA 笔记
自然语言处理的一个重要范式包括对一般领域数据的大规模预训练和对特定任务或领域的适应。当我们预训练更大的模型时,重新训练所有模型参数的完整微调变得不那么可行。LoRA[1]冻结预训练模型权重并将可训练的秩分解矩阵注入到 Transformer 架构的每一层中,大大减少了下游任务的可训练参数的数量。与用 Adam 微调的 GPT-3 175B 相比,LoRA 可以将可训练参数的数量减少了 10,000 倍,GPU 内存需求减少了 3 倍。
什么是low-rank
首先需要明确一些什么什么是矩阵的秩,rank
在国内的本科线性代数课程中我们是这样定义矩阵的秩的
设在矩阵\(A\) 中有一个有一个不等于\(0\) 的\(r\) 阶子式\(D\) ,且所有\(r+1\) 阶子式(如果存在的话)都等于\(0\) ,那么\(D\) 称为矩阵\(A\) 的最高阶非零子式,数\(r\) 成为矩阵的秩,记为\(R(A)\) 。并规定零矩阵的秩为0。[2]
怎么求矩阵的秩呢,很简单啦就是把一个矩阵化成RREF(课本上管这个叫行最简行矩阵)然后数一下每一行第一个非零元素所在列为单位向量的个数就可以了。
好的,发生了什么?好像并没有解释清楚秩到底是什么。
实际上啊,秩反映了矩阵里列向量线性相关的程度,意思就是你矩阵里的那几个向量能“支”出来几维,假如说我有一个矩阵里面有五个向量,但是他的矩阵秩是3,这就说明五个向量只能撑起一个3维空间,剩下两个向量可以被三个不能被互相表示的向量表示(课本上管这个叫线性相关和线性无关),用李宏毅的话说就是这里有两个向量在"耍废"。
推荐一下3Blue1Brown的视频https://www.bilibili.com/video/BV1ys411472E/?spm_id_from=333.999.0.0,线性代数讲的很清楚。
该清楚了秩是什么,低秩是什么就很好理解了,就是有个矩阵他的秩很低,小于矩阵里面向量的个数(向量组线性相关/有向量在"耍废")。
你可能会想问,LoRA作为一个微调大语言模型和图文大模型的方法,关矩阵的秩什么事?在2020年,[3] 指出大模型的训练实际发生在low-rank空间上的,所以说我们只需要构造一个低秩空间下的训练方法就可以了。
为什么需要LoRA
LoRA并不是第一个进行微调大模型的,从迁移学习开始有很多的尝试,以语言建模为例,在有效适应方面有两种突出的策略:添加适配器层或优化某种形式的输入层激活。然而,这两种策略都有其局限性,尤其是在大规模和延迟敏感的生产场景中。
添加适配器层(引入推理延迟)
适配层(Adapter) 实际上就是在原本的架构上添加一些层,让他学到新的东西。例如[4]

左侧为每个 Transformer 层添加适配器模块两次:在多头注意力的投影和两个前馈层之后。右侧适配器由一个瓶颈组成,该瓶颈包含相对于原始模型中的注意力层和前馈层的参数很少。适配器还包含跳过连接。在适配器调整期间,绿色层在下游数据上进行训练,这包括适配器、层归一化参数和最终分类层(图中未显示)。
虽然可以通过修剪层或利用多任务设置来减少整体延迟,但没有直接的方法绕过适配器层中的额外计算。在单个 GPU 上对 GPT-2介质运行推理,我们看到在使用适配器时延迟显着增加,即使瓶颈维度非常小。
优化某种形式的输入层激活(很难进行)
作者观察到前缀调整很难优化,并且它的性能在可训练参数中非单调地变化,证实了原始论文中的类似观察结果。更根本的是,保留序列长度的一部分进行适应必然会降低可用于处理下游任务的序列长度,所以作者怀疑与其他方法相比,调整提示的性能较低。
LoRA到底怎么工作
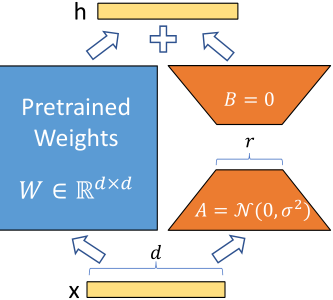
神经网络包含许多执行矩阵乘法的密集层。这些层中的权重矩阵通常具有满秩。对于预训练的权重矩阵 \(W_0 ∈ R^{d×k}\),我们通过使用低秩分解 \(W_0 + ΔW = W_0 + BA\) 表示后者来约束其更新,其中 \(B ∈ R^{d×r} , A ∈ R^{r×k}\),秩\(r\) 为 \(min(d, k)\)。在训练期间,\(W_0\) 被冻结并且不接收梯度更新,而 \(A\) 和 \(B\) 包含可训练的参数。注意 \(W_0\) 和 \(ΔW = BA\) 都乘以相同的输入,它们各自的输出向量按坐标求和。对于 \(h = W_0x\),我们修改后的前向传递产生:$$h=W_0x+\Delta Wx=W_0x+BAx$$
参数初始化时,我们对 A 使用随机高斯初始化,B 使用零,因此 ΔW = BA 在训练开始时为零。所以 \(\Delta W = BA\) 在训练开始时为零.用\(\frac{\alpha}{r}\) 缩放 \(ΔWx\),其中 \(\alpha\) 是 \(r\) 中的一个常数。在使用 Adam 进行优化时,如果我们适当地缩放初始化,调整 \(\alpha\) 与调整学习率大致相同。因此,我们只需将 \(\alpha\) 设置为我们尝试的第一个 r,而不对其进行调整。当我们改变时,这种缩放有助于减少重新调整超参数的需要
这种微调方式有两个好处
- 完全泛化的微调方式
- 不会引入推理延迟
在推理的时候,只需要把\(B\)和\(A\) 两个矩阵乘起来然后加回到原先的参数矩阵就完成了参数的更新
参考文献
LoRA: Low-Rank Adaptation of Large Language Models. (n.d.). ↩︎
同济大学数学系工程数学-线性代数(第6版)笔记和课后习题(含考研真题)详解. (2015). ↩︎
Aghajanyan, A., Gupta, S., & Zettlemoyer, L. (2021). Intrinsic Dimensionality Explains the Effectiveness of Language Model Fine-Tuning. Proceedings of the 59th Annual Meeting of the Association for Computational Linguistics and the 11th International Joint Conference on Natural Language Processing (Volume 1: Long Papers). Presented at the Proceedings of the 59th Annual Meeting of the Association for Computational Linguistics and the 11th International Joint Conference on Natural Language Processing (Volume 1: Long Papers), Online. https://doi.org/10.18653/v1/2021.acl-long.568 ↩︎
Houlsby, N., Giurgiu, A., Jastrzębski, S., Morrone, B., Laroussilhe, Q., Gesmundo, A., … Gelly, S. (2019). Parameter-Efficient Transfer Learning for NLP. International Conference on Machine Learning. ↩︎