Theories
Markov Decision Process
Generally, we notes a MDP model as \((S, A, T_a, R_a, \gamma)\). Its transition function is \(T_a(s,s')=\Pr(s_{t+1}|s_t=s, a_t=a)\), reward function is \(R_a(s,s')\). And actions choosing satisfies a specific distribution.
The cotinuous decisions are noted as trace \(\tau\), formally in formula:
And in many situations, we very care about the expected reward of a specific trace because that will support us to choose the optimal action currently. So we use the method like weighted time series to calculate cumulative reward:
\[R(\tau_t) = r_t + \gamma r_{t+1} + \gamma^2 r_{t+2} + \cdots=r_t+\sum_{i=1}^\infty \gamma^ir_{t+i} \]After we got the return value of traces, we can just calculate the value of a state to form our policy.
\[V^{\pi}(s)=E_{\tau\sim p(\tau_t)}[\sum_{i=0}^\infty \gamma^ir_{t+i}|s_t=s] \]However, although we can get the value function to form optimal policy, we cann't still calculate the values of all states. So we need Bellmax Equation to solve the problem.
Bellman Equation
\[V^{\pi}(s)=\sum_{a\in A}\pi(a|s)[\sum_{s'\in S}T_a(s,s')[R_a(s,s')+\gamma V^{\pi}(s')] \]For a specific state \(s\), when choosing some action, we will get a stochastic new state which satisfies some distribution. Bellman Equation tells us to calculate the expected average value of these possible new states' return. And in detail, the return of each state have two parts: the immediate reward \(R_a(s,s')\) and the future reward \(\gamma V^{\pi}(s')\). That inspires us that we can calculate the value of states recursively.
Value Iteration
Value Iteration is a method to calculate Bellman Equation by traversing the state and action space. Firstly, it stores a value table of all states. And in traversing process, it will calculate the value of each state and update the value table by choosing the action with the highest return.
Experiments
Taxi Environment of OpenAI Gym
- Taxi Enviroment
The Taxi example is an environment where taxis move up, down, left, and right, and pichup and dropoff passengers. There are four disignated locations in the Grid world indicated by R(ed), B(lue), G(reen), and Y(ellow). - Taxi Activities
In an episode, the taxi starts off at a random square and the passenger is at a random location. The taxi drives to the passenger's location, picks up the passenger, then drives to the passenger's destination(another one of the four specified locations), and drops off the passenger. - States and Actions Space
- \(500=25\times5\times4\) discrete states
With the grid size of \(5 \times 5\), there are \(25\) taxi positions. For the passenger, there are \(5\) possible locations(including the case when the passenger is in the taxi). For the destination, there are \(4\) possible locations. - \(6\) discrete deterministic actions
For the Taxi diver,- \(0\): Move south
- \(1\): Move north
- \(2\): Move east
- \(3\): Move west
- \(4\): Pick up passenger
- \(5\): Drop off passenger
- \(500=25\times5\times4\) discrete states
- Rewards
- \(-1\) for each action
- \(+20\) for delivering the passenger
- \(-10\) for picking up and dropping off the passenger illegally
The following pictures are taxi example demostration. The left shows taxi actions with a random policy and the right shows taxi actions with the optimal policy.
Results
Now we want to check how the discount factor influences the value function from the same start state. So we choosing the discount factor ranging from \(0.0\) to \(1.0\) with footstep of 0.05 to measure the average rewards and cumulative rewards on random group and optimal group.
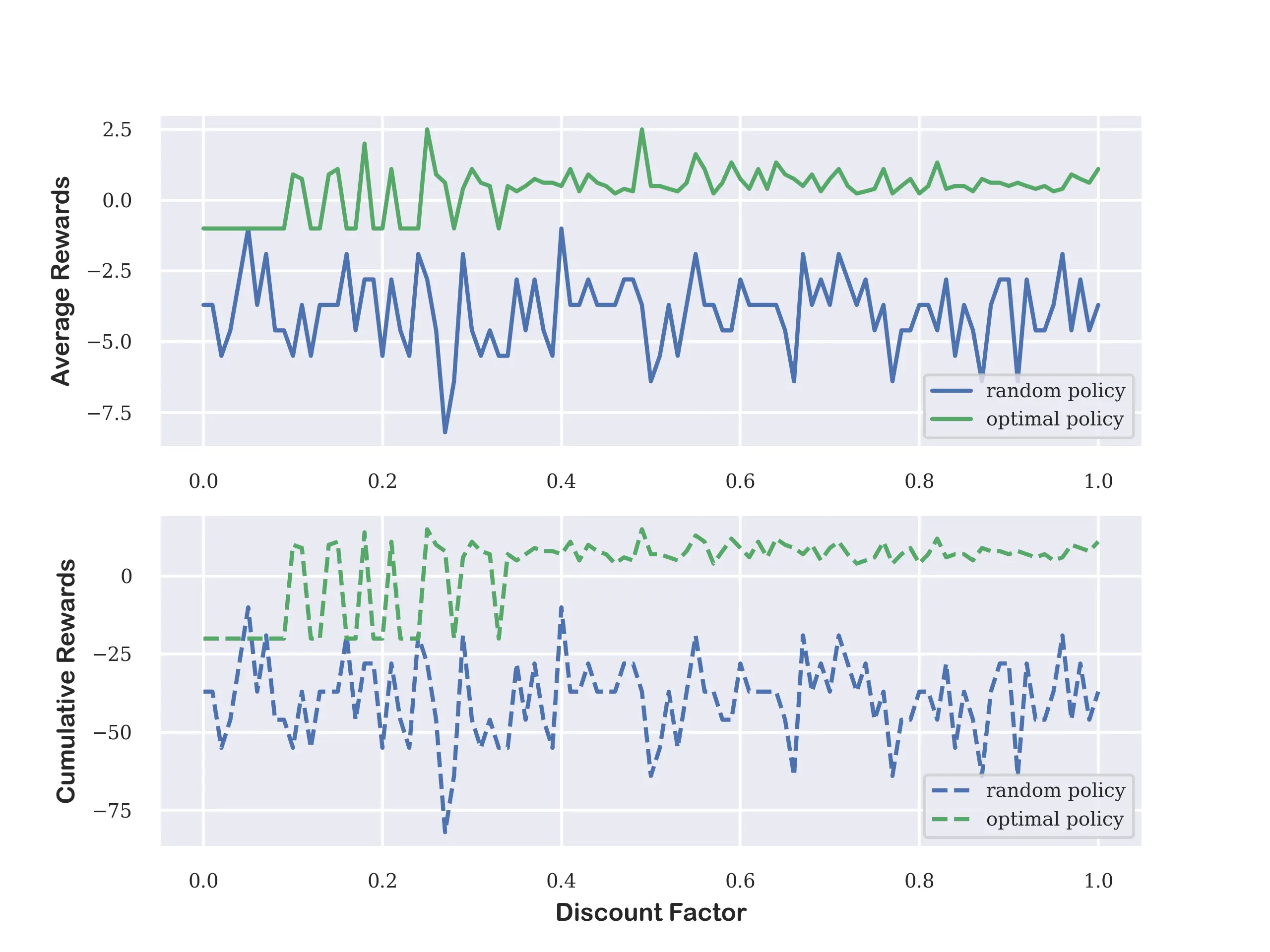
| Discount Factor | Random Cum_Reward | Random_Aver_Reward | Optimal Cum_Reward | Optimal_Aver_Reward |
|---|---|---|---|---|
| 0.00 | -37 | -3.70 | -20 | -2.00 |
| 0.05 | -10 | -1.00 | -20 | -1.00 |
| 0.10 | -55 | -5.50 | 10 | 0.91 |
| 0.15 | -37 | -3.70 | 11 | 1.10 |
| 0.20 | -55 | -5.50 | -20 | -1.00 |
| 0.25 | -28 | -2.80 | 15 | 2.50 |
| 0.30 | -46 | -4.60 | 11 | 1.10 |
| 0.35 | -28 | -2.80 | 5 | 0.31 |
| 0.40 | -10 | -1.00 | 7 | 0.50 |
| 0.45 | -37 | -3.70 | 7 | 0.50 |
| 0.50 | -64 | -6.40 | 7 | 0.50 |
| 0.55 | -19 | -1.90 | 13 | 1.60 |
| 0.60 | -28 | -2.80 | 9 | 0.75 |
| 0.65 | -46 | -4.60 | 10 | 0.91 |
| 0.70 | -37 | -3.70 | 9 | 0.75 |
| 0.75 | -46 | -4.60 | 6 | 0.40 |
| 0.80 | -37 | -3.70 | 4 | 0.24 |
| 0.85 | -37 | -3.70 | 7 | 0.50 |
| 0.90 | -28 | -2.80 | 7 | 0.50 |
| 0.95 | -37 | -3.70 | 5 | 0.31 |
| 1.00 | -37 | -3.70 | 11 | 1.10 |
Conclusions
From the following experimental results, we can conclude that the discount factor has a significant impact on the value function. The optimal group has a higher average and cumulative reward than the random group, and the discount factor has a lower bound \(\gamma=0.4\) to get optimal policy.
In my opinion, the discount factor reflects the future reward's influence on the current state. If it is set too small, that means the most reward comes from the immediate reward which is a greedy policy with the possibility of failure. On the other hand, if set too high, we also cann't get the best action with the highest reward. So we'd better to set the discount factor to an appropriate value.
Codes
from argparse import ArgumentParser
class BaseOptions:
def __init__(self):
self.parser = ArgumentParser()
self.parser.add_argument('--algorithm', type=str, default='ValueItration')
self.parser.add_argument('--n_rounds', type=int, default=500, help='Number of rounds')
self.parser.add_argument('--ub_gamma', type=float, default=1, help='upper bound of discount factor')
self.parser.add_argument('--lb_gamma', type=float, default=0, help='lower bound of discount factor')
self.parser.add_argument('--NA', type=int, default=6, help='Length of Actions Space')
self.parser.add_argument('--NS', type=int, default=500, help='Length of States Space')
self.parser.add_argument('--end_delta', type=float, default=0.00001, help='end delta')
self.parser.add_argument('--print_interval', type=int, default=50, help='print interval')
def parse(self):
return self.parser.parse_args()
"""
-------------------------------------------------------
Project: Solving as MDP using Value Iteration Algorithm
Author: Zhihao Li
Date: October 19, 2023
Research Content: Deep Reinforcement Learning
-------------------------------------------------------
"""
from options import BaseOptions
from value_iteration import ValueMDP
import gym # openAi gym
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from matplotlib.font_manager import FontProperties
import warnings
warnings.filterwarnings('ignore')
# Set up Seaborn style
sns.set(style="darkgrid")
Efont_prop = FontProperties(fname="C:\Windows\Fonts\ARLRDBD.TTF")
label_prop = FontProperties(family='serif', size=7, weight='normal')
legend_font = FontProperties(family='serif', size=7, weight='normal')
if __name__ == '__main__':
opts = BaseOptions().parse() # set project's options
# Set OpenAI Gym environment
env = gym.make('Taxi-v3', render_mode="rgb_array")
gamma_delta = 0.01
aver_rewards = np.zeros(len(np.arange(opts.lb_gamma, opts.ub_gamma + gamma_delta, gamma_delta)))
random_aver_rewards = np.zeros(aver_rewards.shape)
cum_rewards = np.zeros(aver_rewards.shape)
random_cum_rewards = np.zeros(aver_rewards.shape)
for t, gamma in enumerate(np.arange(opts.lb_gamma, opts.ub_gamma + gamma_delta, gamma_delta)):
# Init env and value iteration process
VIMDP = ValueMDP(env, opts, gamma)
# Apply the random policy
VIMDP.env.reset(seed=t+101)
VIMDP.ApplyRandomPolicy(steps=10)
# Value Iteration in MDP
observation = VIMDP.env.reset(seed=t+101)
VIMDP.IterateValueFunction()
# Apply the optimal policy
VIMDP.ApplyOptimalPolicy(observation[0], steps=20)
# Save reward results
aver_rewards[t] = VIMDP.aver_reward
random_aver_rewards[t] = VIMDP.random_aver_reward
cum_rewards[t] = VIMDP.cum_reward
random_cum_rewards[t] = VIMDP.random_cum_reward
print("discount factor: %f" % gamma)
print("Applying the random policy, accumulated reward: %.5f, average reward: %.5f" % (random_cum_rewards[t], random_aver_rewards[t]))
print("Applying the optimal policy, accumulated reward: %.5f, average reward: %.5f" % (cum_rewards[t], aver_rewards[t]))
# plot the rewards
xdata = np.arange(opts.lb_gamma, opts.ub_gamma + gamma_delta, gamma_delta)
plt.subplot(211)
plt.plot(xdata, random_aver_rewards, 'b-', label='random policy')
plt.plot(xdata, aver_rewards, 'g-', label='optimal policy')
plt.ylabel('Average Rewards', fontproperties=Efont_prop, fontsize=9)
plt.yticks(fontproperties=label_prop, fontsize=7)
plt.xticks(fontproperties=label_prop, fontsize=7)
plt.legend(loc='lower right', fontsize=7, prop=legend_font)
plt.subplot(212)
plt.plot(xdata, random_cum_rewards, 'b--', label='random policy')
plt.plot(xdata, cum_rewards, 'g--', label='optimal policy')
plt.xlabel('Discount Factor', fontproperties=Efont_prop, fontsize=9)
plt.ylabel('Cumulative Rewards', fontproperties=Efont_prop, fontsize=9)
plt.yticks(fontproperties=label_prop, fontsize=7)
plt.xticks(fontproperties=label_prop, fontsize=7)
plt.legend(loc='lower right', fontsize=7, prop=legend_font)
plt.savefig("Rewards.png", dpi=400)
env.close()
import numpy as np
"""
--------------------------------------------------------------------------------------
This section is for Value Iteration Algorithm for Taxi Gym.
Author: Zhihao Li
Date: October 19, 2023
Arguments:
env: OpenAI env. env.P represents the transition probabilities of the environment.
env.P[s][a] is a list of transition tuples (prob, next_state, reward, done).
end_delta: Stop evaluation once value function change is less than end_delta for all states.
discount_factor: Gamma discount factor.
--------------------------------------------------------------------------------------
"""
class ValueMDP:
def __init__(self, env, opts, gamma) -> None:
self.env = env # taxi gym environment
self.gamma = gamma # discount_factor
self.NA = opts.NA # Actions Space's Length
self.NS = opts.NS # States Space's Length
self.V = np.zeros(self.NS) # Value Function
self.end_delta = opts.end_delta # Delta value for stopping iteration
self.new_policy = np.zeros(self.NS) # the optimal policy
self.cum_reward = 0 # apply new policy and get all rewards
self.aver_reward = 0
self.random_cum_reward = 0 # rewards applying random actions
self.random_aver_reward = 0
def SingleStepIteration(self, state):
"""
Function: calculate the state value for all actions in a given state
and update the value function.
Returns:
The estimate of actions.
"""
action_V = np.zeros(self.NA) # Record the value of each action
for action in range(self.NA):
for prob, nextState, reward, is_final in self.env.P[state][action]:
action_V[action] += prob * (reward + self.gamma * self.V[nextState] * (not is_final))
return action_V
def IterateValueFunction(self):
while True:
delta = 0 # initialize the every round of delta
for s in range(self.NS):
newValue = np.max(self.SingleStepIteration(s))
delta = max(delta, np.abs(newValue - self.V[s]))
self.V[s] = newValue # updates value function
if delta < self.end_delta: # the maximum delta of all states
break
# get optimal policy
for s in range(self.NS): # for all states, create deterministic policy
newAction = np.argmax(self.SingleStepIteration(s))
self.new_policy[s] = newAction
def ApplyOptimalPolicy(self, observation, steps):
for i in range(steps):
action = self.new_policy[observation]
observation, reward, is_final, truncated, info = self.env.step(np.int8(action))
self.cum_reward += reward
# self.env.render()
if is_final:
break
self.aver_reward = self.cum_reward / (i + 1)
def ApplyRandomPolicy(self, steps):
for i in range(steps):
observation, reward, is_final, truncated, info = self.env.step(self.env.action_space.sample())
self.random_cum_reward += reward
# self.env.render()
if is_final:
break
self.random_aver_reward = self.random_cum_reward / (i+1)