前置知识:
复数,单位根,多项式乘法,点值表示法,系数表示法 \(\cdots\)
单位根:
首先,我们在一个复平面中定义一个单位圆,将单位圆等分为 \(n\) 份,把位于单位圆上幅角为正且最小的向量定义为 \(n\) 次单位根,记为 \(\omega_n\)。
那我们来考虑一下单位根的奇妙性质:
首先根据复数的运算法则,两个复数相乘可以转化为复平面上的两个向量幅角相加,模长相乘,因此 \(\omega_{k=0,1,2 \cdots n}\) 实际上就是 \(\omega_n^{k=0,1,2 \cdots n}\),当然它们也是方程 \(x^n=1\) 的根。
放一下这个经典图:
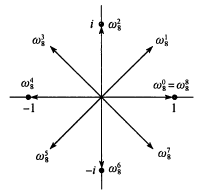
根据欧拉公式:
性质1
- \[\omega_{2n}^{2k}=\omega_{n}^{k} \]
\[\begin{aligned} \omega_{2n}^{2k}&=\cos\frac{2\pi\times2k}{2n}+i\sin\frac{2\pi\times2k}{2n}\\ &=\cos\frac{2\pi\times k}{n}+i\sin\frac{2\pi\times k}{n}\\ &=\omega_{n}^{k} \end{aligned}\]证明:
性质2
- \[\omega_{n}^{\frac{n}{2}+k}=-\omega_{n}^{k} \]
\[\begin{aligned} \omega_{n}^{\frac{n}{2}}&=\cos\frac{2\pi\times\frac{n}{2}}{n}+i\sin\frac{2\pi\times\frac{n}{2}}{n}\\ &=\cos{\pi}+i\sin{\pi}\\ &=-1 \end{aligned}\]证明:
性质3
- \[ \sum\limits_{i=0}^{n-1}(\omega_n^k)^i=\left\{ \begin{aligned} n (k=0)\\ 0 (k\ne0) \end{aligned} \right. \]
证明:
当 \(k\neq 0\) 时,根据等比数列求和:
\[\sum\limits_{i=0}^{n-1}(\omega_n^k)^i=\frac{1-\omega_n^{nk}}{1-\omega_n^k}=0 \]因为 \(k\neq 0\) 所以保证了上式的分母不为 \(0\)。
当 \(k=0\) 时,显然原式为 \(n\)。
多项式乘法:
定义卷积为如下的一种关系:
\[h(k)=f*g=\sum_{i\circ j=k} f_i g_j \]其中 \(i\circ j=k\) 表示一种下标运算法则,当这个关系为 \(i+j=k\) 时,这就是多项式的乘法啦。
多项式表示法:
- 系数表示法:
就是常见的多项式表示法:\(\sum\limits_{i=0}^{n-1}a_ix^i\) 这样我们会获得一个 \(\Theta(n^2)\) 多项式乘法。 - 点值表示法:
设原多项式为 \(H(x)\),我们用 \(\{(x_0,H(x_0)),(x_1,H(x_1)),(x_2,H(x_2))\cdots(x_n,H(x_0))\}\) 来描述一个多项式,这样两个多项式 \(H(x)\) 与 \(F(x)\) 的乘积就可以很轻松的表示为 \(\{(x_0,F(x)H(x_0)),(x_1,F(x)H(x_1)),(x_2,F(x)H(x_2))\cdots(x_n,F(x)H(x_0))\}\),对于单个点值可以 \(\Theta(n)\) 求解。
傅里叶变换
在开始之前,我们可以区分一下各种变换:
\(DFT\):离散傅里叶变换 \(\rightarrow \Theta(n^2)\) 计算多项式乘法
\(FFT\):快速傅里叶变换 \(\rightarrow\Theta(n\log n)\) 计算多项式乘法
\(FNTT/NTT\):快速傅里叶变换的优化版 \(\rightarrow\) 优化常数及误差
\(FWT\):快速沃尔什变换 \(\rightarrow\) 利用类似FFT的东西解决一类卷积问题
\(FMT\):快速莫比乌斯变化
离散傅里叶变换
我们发现常规暴力卷积复杂度是 \(\Theta(n^2)\) 的,看起来很难优化,但是用点值表示法的多项式单次乘法可以 \(\Theta(n)\) 实现,虽然带入 \(n\) 个点依然是 \(\Theta(n^2)\) 的复杂度,但至少有着优化的可能。不过,一个点值表示的多项式没有太大价值,只有系数表示法的多项式才能有更加广泛的应用。因此,这启发我们寻找这样一个算法体系解决多项式乘法:先将系数表示法转为点值表示法,优化卷积,再将结果转回系数表示法,怎么办?
傅里叶想出用 \(n\) 个模长为1的复数与点值表示法来描述多项式,而这 \(n\) 个复数选取复平面单位圆上的 \(n\) 个等分点,也就是 \(\omega_n^k(k=0,1,2\cdots n-1)\),这样也就实现了第一步:将系数表示法转为点值表示法,这也就是 \(DFT\),即:
我们设 \(\vec{a}=(a_0,a_1,a_3\cdots a_n)\) 是原多项式 \(A(x)\) 的系数表达:
\[y_k=\sum_{i=1}^{n-1}\omega_n^{ki}a_i \]那么 \(\vec{y}=(y_0,y_1,y_3\cdots y_n)\) 即为 \(DFT_n(\vec{a})\)
那为什么要带入这个 \(\omega_n^i\)?这是因为单位根有着优美的性质,可以很好的实现点值表示法转为系数表示法,即 \(IDFT\)。这就要引出离散傅里叶变换的一个重要结论:把多项式 \(A(x)\) 的离散傅里叶变换结果作为另一个多项式 \(B(x)\) 的系数,取单位根的倒数带入 \(B(x)\),将结果除以 \(n\) 就是 \(A(x)\) 的各项系数,我们来证明一下:
设 \(IDFT_n(\vec{y})=\vec{z}\),则有:
\[\begin{aligned} z_k&=\frac{1}{n}\sum_{i=0}^{n-1}y_i(\omega_n^{-k})^i\\ &=\frac{1}{n}\sum_{i=0}^{n-1}(\sum_{j=0}^{n-1}{(\omega_n^{ij}a_j)})(\omega_n^{-k})^i\\ &=\frac{1}{n}\sum_{i=0}^{n-1}\sum_{j=0}^{n-1}{(\omega_n^{ij}a_j)}(\omega_n^{-ki})\\ &=\frac{1}{n}\sum_{i=0}^{n-1}\sum_{j=0}^{n-1}a_j(\omega_n^{ij}\omega_n^{-ki})\\ &=\frac{1}{n}\sum_{j=0}^{n-1}a_j\sum_{i=0}^{n-1}(\omega_n^{j-k})^i\\ &=\sum_{j=0}^{n-1}a_j(\frac{1}{n}\sum_{i=0}^{n-1}(\omega_n^{j-k})^i) \end{aligned}\\ \]根据上文关于单位根的性质3的探究,我们知道:
\[\frac{1}{n}\sum_{i=0}^{n-1}(\omega_n^{j-k})^i=\left\{ \begin{aligned} 1 (j=k)\\ 0 (j\ne k) \end{aligned} \right. \]因此有
\[\begin{aligned} z_k&=a_k\\ \vec{z}&=\vec{a} \end{aligned} \]\(\Box\)
快速傅里叶变换
经过上述运算我们的的确确的找到了一种算法的雏形,但它的暴力卷积依然是 \(\Theta(n^2)\) 的,我们来优化这个算法:
首先,我们将多项式 \(A(x)=\sum\limits_{i=0}^{n-1}a_ix^i\) 以奇偶划分开来,那么我们得到两个新的多项式 \(A_1\) 和 \(A_2\):
\[\begin{aligned} A_1(x)&=a_0+a_2x^1+a_4x^2+a_6x^3+\cdots+a_{n-2}x^{n/2-1}\\ A_2(x)&=a_1+a_3x^1+a_5x^2+a_7x^3+\cdots+a_{n-1}x^{n/2-1} \end{aligned} \]显然有
\[\begin{aligned} A(x)=A_1(x^2)+xA_2(x^2) \end{aligned} \]这样的递推关系显然启示我们分治来解决问题,那么此时原式的 \(DFT_n(A)\) 被分治到了 \(DFT_{n/2}(A_1)\) 和 \(DFT_{n/2}(A_2)\),那我们不妨将 \(\vec{\omega}_n\) 分别代入 \(A_1\) 与 \(A_2\) 考虑:
标签:frac,多项式,sum,FFT,表示法,关于,aligned,omega From: https://www.cnblogs.com/shen666zxcmt/p/17796661.html