关于 wqs 二分的几何意义的思考

我们知道，wqs 二分是通过二分斜率，通过找到切凸包的切点来寻找答案（至少我目前写的简单题是这样的）。那么所谓切凸包的几何意义是什么？我们以 LG P5633 最小度限制生成树 为例。

对于样例，我们设 \(f(x)\) 为节点 \(s\) 恰为 \(x\) 度的情况下最小生成树的权值，画出凸包。

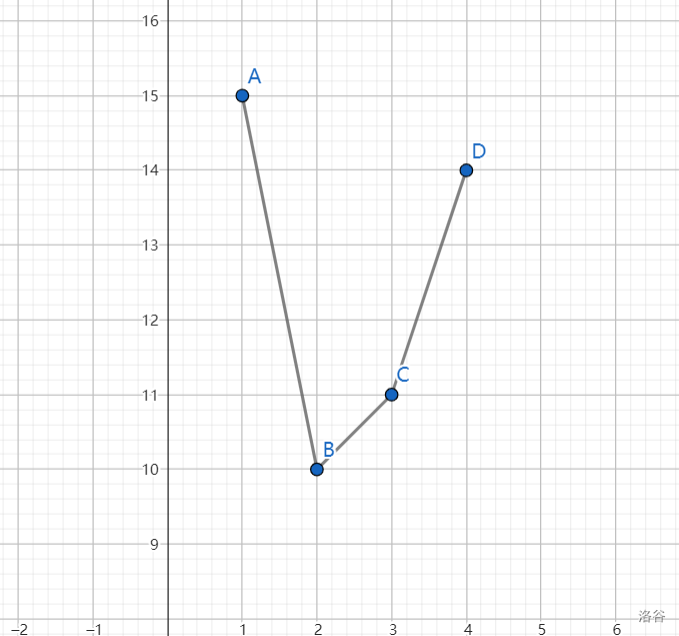
由于偏移量是平滑的，直觉上看，当偏移量不断变化时，所形成的最小生成树的权值也应当是平滑变化的。结合偏移量与凸包之间斜率的关系，我们可以画出下面这张图：

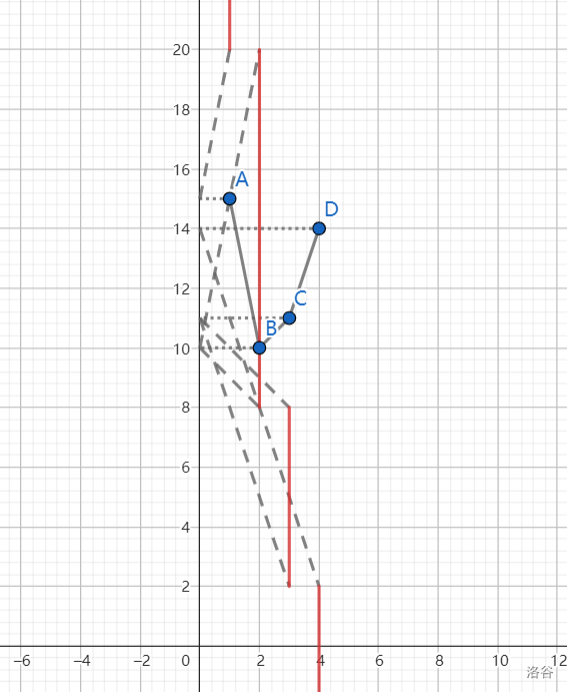
为什么？首先，赋予 \(s\) 边的偏移量越小，意味着 \(s\) 边的权值越小，那么构造 \(\text{MST}\) 时就会倾向于选用更多的 \(s\) 边。其次，证一个引理：无论赋予 \(s\) 边的偏移量多少，若钦定了生成的 \(\text{MST}\) 中含 \(s\) 边的数量不变（即钦定生成的必须是恰含 \(k\) 条 \(s\) 边的情况下的 \(\text{MST}\)），那么它的形态一定不会变（若同时有多个 \(\text{MST}\)，那么偏移量变化后也都仍然是 \(\text{MST}\)）。这是显然的，若偏移量加上了 \(\Delta\)，那么对于所有含 \(k\) 条 \(s\) 边的最小生成树，它们的权值都加上了 \(k \cdot \Delta\)，那么显然原来最小的现在仍然最小，故形态不变。那么，对于原来的凸包，我们将凸包上的点的纵坐标对应到纵轴上。由引理，我们知道将 \((x_0, f(x_0))\) 射影到纵轴上，过该点任作一条直线 \(y = kx + f(x_0)\)，其与直线 \(x = x_0\) 的交点的纵坐标就是赋予 \(s\) 边的偏移量为 \(k\) ，且恰选 \(x_0\) 条 \(s\) 边时最小生成树的权值，这是因为，交点的纵坐标为 \(f(x_0) + kx_0\)，就对应着 \(x_0\) 条 \(s\) 边加上总偏移量 \(kx_0\) 的情况下的最小值。那么对于一个斜率 \(k\)，我们将纵轴上每个射影的点都做一条斜率为 \(k\) 的直线，这些直线交 \(x = x_{i}\) 中纵坐标最小的交点，对应的就是当前偏移量为 \(k\) 的情况下最小生成树的权值：

红线表示当点在红线上时，它的纵坐标是最小的。这张图反映了当偏移量减小时，\(\text{MST}\) 会倾向选用更多的 \(s\) 边（即与横坐标更大的直线相交的纵坐标更小），且生成的最小生成树权值的变化是平滑的（纵坐标最小的点变化时红线组成了连续段）。于是我们应该研究这些红线跳变的纵坐标，此时会发现：对于横坐标为 \(x_0\) 的红线，它由这个点所对应的 \(f(x_0)\) 与凸包相邻两点的斜率决定，是将凸包上的点 \((x, f(x_0))\) 射影到纵轴上后，过射点分别作斜率为原本的点与相邻两点间斜率的相反数的直线与 \(x = x_0\) 的交点组成的线段。或者另一种生成方式：过凸包上的一点作所有切线与纵轴的交点组成的线段，对应到原本的横坐标上。例如只考虑点 \(C\) 对应的红线：

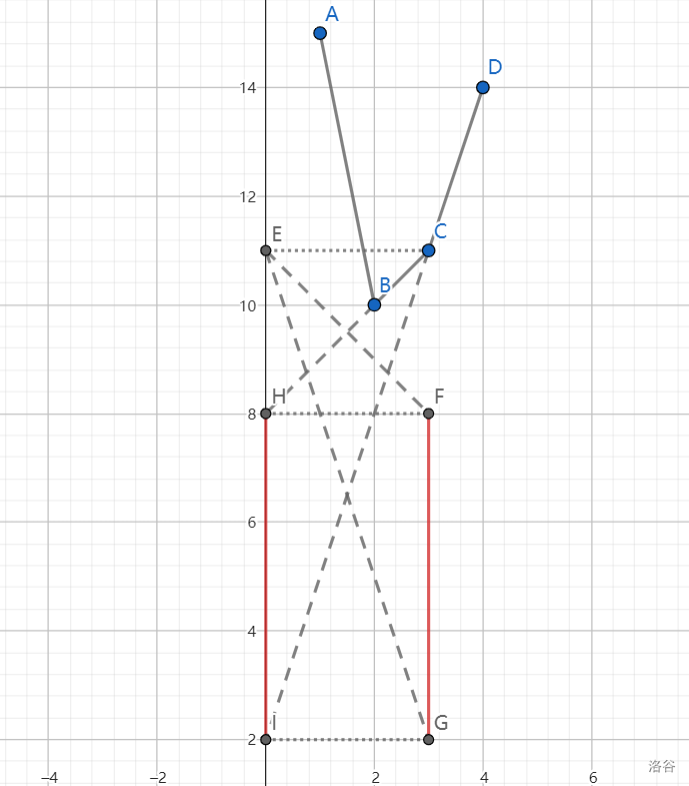
图中 \(k_{EF} = -k_{BC}\)，\(k_{EG} = -k_{CD}\)。

为什么？首先显然当 \(k\) 不断减小时，交点纵坐标是在减小的。并且由于这是个下凸壳，凸壳间的斜率是不断增大的，那么其斜率的相反数不断减小。射点都在纵轴上，斜率相同时，其交的直线距离纵轴越远（即 \(x_0\) 越大），根据相似对应，其交点的变化速率也应当越快。那么我们只需考虑相邻两个交点在什么时候纵坐标相同。不妨考虑上图中的 \(B\)、\(C\) 两点：设 \(B'(x_0, f(x_0) + k \cdot x_0)\)，\(C'(x_0 + 1, f(x_0 + 1) + k \cdot(x_0 + 1))\)，当 \(k = -(\displaystyle \frac{f(x_0 + 1) - f(x_0)}{x_0 + 1 - x_0}) = f(x_0) - f(x_0 + 1)\) 时，有 \(B'(x_0, (x_0 + 1)f(x_0) - x_0f(x_0 + 1))\)，\(C'(x_0 + 1, (x_0 + 1)f(x_0) - x_0f(x_0 + 1))\)，两点纵坐标相等，于是当 \(k\) 减小时，\(C'\) 即从此刻开始超过 \(B'\)，变成新的纵坐标最小的点。这或许是 wqs 二分中二分的斜率的意义：当斜率减小至超过某数 \(k_0\) 时，选取的关键边过多，于是增加斜率；反之减小斜率，根据所交的点减去 \(\text{关键边数} \cdot k\) 即可还原出凸包上的点，其成立的关键应当就是图中红边的连续性，而答案凸包中相邻的斜率的相反数就对应着此时关键边数的跳变。

关于凸包中相邻两点斜率的几何意义，我的想法是，不妨设凸包中一点为 \((x, f(x))\)，另一点为 \(x + 1, f(x) + \Delta\)，那么它们间的斜率为 \(\Delta\)。假设当 \(k = k_0\) 时两点对应的红线发生了跳变，那么 \(f(x) + xk_0 = f(x) + \Delta + (x + 1)k_0\)，相减得 \(\Delta = -k_0\)，\(\Delta\) 的意义应当是若恰多选一条关键边，那么方案的价值增加了 \(\Delta\)，而 \(k = k_0\) 时发生跳变，意味着当 \(k = k_0\) 时恰多选一条关键边，原有 \(x\) 条关键边，那么 \(f(x) + xk_0\) 与 \(f(x) + \Delta + (x + 1)k_0\) 是相同的，感性理解，此时从这点“减去” \((x + 1)k_0\) 与 \(xk_0\) 恰好差了 \(\Delta\)。所以 \(k_0\) 的生成会跟 \(\Delta\) 有关。所谓的二分斜率，其实二分的是偏移量的相反数（\(z_1 = f(x_0) - k_1x_0\) 与 \(z_2 = f(x_0) + k_2x_0\)，\(k_1 = -k_2\) 的区别，\(k_1\) 是答案凸包上的斜率，\(k_2\) 是偏移量）。