斜率优化是一种优化 \(dp\) 的方法,不过在哪之前,我们需要引入一道例题。
点击查看代码
给你一个长度为 $n$ 序列 $A$,你需要把他分成若干段。定义第 $x$ 段的贡献为: $$a \times(\sum_{i=l_x}^{r_x} a_i))^2 +b\times \sum_{i=l_x}^{r_x} a_i+c$$ 你需要最大化贡献。 $a,b,c$ 为给定常数。 $n \leq 10^6$。首先不妨先思考 \(O(n^2)\) 复杂度怎么做,我们不妨定义 \(f_{i}\) 表示以 \(i\) 结尾的最大贡献。显然存在 \(f_{i} = \max \limits _{j=1}^i \{ f_{i},f_{j-1}+a \times sum^2+b\times sum+c\}\) 。我们定义 \(sum\) 表示 \(\sum\limits_{k=j}^i a_k\)。显然,我们需要优化。
这时候引入斜率优化,不妨将转移点设为 \(k\),那么就会有这样一个式子。\(f_i=f_{k}+sum\times a+sum^2\times b+c\)。我们定义 \(s_i = \sum \limits _{j=1}^i a_j\)。原来的式子就会被我们变为: \(f_{i}=f_{k}+(s_{i}-s_{k-1})^2\times a+(s_{i}-s_{k-1})\times b+c\)。
这个式子是可以看做一个一次函数的,我们不妨设 \(s_{k-1}\) 为 \(x\),这样原来的式子就可以看为:
\(f_i=f_k+(s_i-x)^2\times a+(s_i-x)\times b+c\) 。
发现没有?我们把这个玩应打开。
\(f_{i}=f_{k}+as_i^2-2as_ix+x^2a+s_ib-xb+c\)。
我们其实不需要在乎 \(as_i^2+s_ib+c\) 这个东西,因为对于两个转移点 \(j,k\) 来说,这一个部分都是相同的,真正决定大小的显然并不是这一个地方。
也就是说,假设存在两个点 \(j,k\),如果 \(j\) 比 \(k\) 更优,就一定说明是 \(f_j+2as_is_j+as_j^2-bs_j \gt f_{k}+2as_is_k+as_k^2-bs_k\)
这个地方更优秀。
我们继续沿用刚才的思路,设 \(s_j,s_k\) 为 \(x_1,x_2\)。原来的式子就相当于
\(f_j+2as_jx_1+ax_1^2-bx\gt f_k+2as_ix_2+ax_2^2-bx_2\) 。
这时候就是斜率优化要做的事情了。我们可以把式子改成:
\(2as_ix_1-2as_ix_2\gt f_k-f_j+ax_2^2-ax_1^2-bx_2+bx_1\)
但是还没完,\(a\lt 0\)!!!
所以我们要变号。
\(2as_ix_1-2as_ix_2\lt f_k-f_j+ax_2^2-ax_1^2-bx_2+bx_1\)
也就是说 \(j\) 比 \(k\) 更优只需要满足这个式子就好了。由于我们 \(a\lt 0\),\(j,k\) 两点的式子又有单调性。所以本质上我们的最优答案就可以看成一个图。
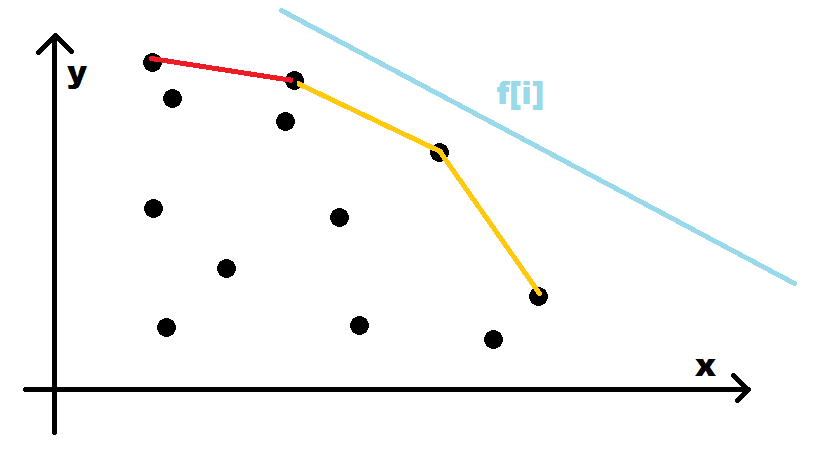
不难发现,这是一个凸包,又具有单调性,我们可以使用单调队列维护。
具体的,我们每一次都是用队头更新答案(看图你会发现这道题这个东西单调递减)。在更新答案时,我们维护队头元素的点即可。使用我们前面推的式子即可轻松维护。同时,为了保证最优性,所以我们还需要在队尾也这样写。
Code
#include<bits/stdc++.h>
//fj-fk+a(sumj^2-sumk^2)-b(sumj-sumk)/2a*(sumj-sumk) <sumi
using namespace std;
#define int long long
const int Maxn=2e6;
int n,aa,b,c,Sum[Maxn],per[Maxn],dp[Maxn],l,r,q[Maxn];
double slove(int j,int k){
return double( (dp[j]-dp[k]+aa*(Sum[j]*Sum[j]-Sum[k]*Sum[k])+b*(Sum[k]-Sum[j]))/double(2*aa*(Sum[j]-Sum[k])) );
}
signed main(){
cin>>n;
cin>>aa>>b>>c;
for(int i=1;i<=n;i++){
cin>>per[i];
Sum[i]=Sum[i-1]+per[i];
}
//memset(dp,~0x3f,sizeof(dp));
dp[0]=0;
l=r=1;
for(int i=1;i<=n;i++){
while(l<r&&slove(q[l],q[l+1])<=1.0*Sum[i])l++;
dp[i]=dp[q[l]]+(Sum[i]-Sum[q[l]])*(Sum[i]-Sum[q[l]])*aa+b*(Sum[i]-Sum[q[l]])+c;
while(l<=r&&slove(q[r-1],q[r])>=slove(q[r],i)) r--;
q[++r]=i;
}
cout<<dp[n];
return 0;
}