思路
我们需要尽量让相邻两个数的和的最大值减最小值最小。
先思考如何让最大值最小。
对于 \(n\),两侧最小也必须要放 \(1\) 和 \(2\)。所以最大值至少也是 \(n+2\)。
同时,我们再思考 \(1\) 周围能摆什么,因为不能让最小值太小,我们需要放比较大的,也就是 \(n\) 和 \(n-1\)。
这样来看的话,最小值最大是 \(n\)。
所以除了 \(n=1\) 或者 \(n=2\) 的特殊情况外,我们要构造的序列的值最小是 \(2\)。
再来思考一下能不能达成 \(2\),对于大于 \(\lceil\frac n 2\rceil\) 的 \(i\),他的两侧可以放 \(n-i+2\) 和 \(n-i+1\)。对于小于 \(\lfloor \frac n 2\rfloor\) 的 \(i\),他的两侧可以放 \(n-i+1\) 和 \(n-i\)。可以验证这样摆放再处理一下 \(n\) 为偶数的特殊情况,就可以使值为 \(2\)。
那么,我们在思考如何生成序列。
首先可以确定 \(n\) 的位置,在它的两侧放上 \(1\) 和 \(2\),再在 \(1\) 旁边的空位摆上 \(n-1\),在 \(2\) 旁边的空位摆上 \(n-2 \cdots\)。
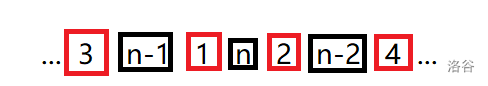
可以发现,这种构造方式可以换一种描述方式。
先摆一个 \(n\),然后每次在两侧加数,第 \(2\times k-1\) 次加数会在两侧分别加 \(2\times k-1\) 和 \(2\times k\),第 \(2\times k\) 次加数会在两侧分别加 \(n-2\times k+1\) 和 \(n-2\times k\)。
如果最后还剩一个也就是 \(n\) 为偶数时,可以把剩下的数放在任意两端。
AC code
#include<bits/stdc++.h>
using namespace std;
int n,a,b[1000005],now,cnt=1,mi,ma,ha;
int main()
{
scanf("%d",&n),now=n,mi=1,ma=n-1,ha=ceil(1.0*n/2),b[ha]=n;//懒得算每次摆的是什么数,于是就用两个变量存一下,ha记录中间的位置
while(cnt<=(n-1)/2)
if(cnt&1) b[ha-cnt]=mi,b[ha+cnt]=mi+1,mi+=2,++cnt;
else b[ha-cnt]=ma,b[ha+cnt]=ma-1,ma-=2,++cnt;//按照上面的方法摆放数字
if(n%2==0) b[n]=mi;//n为偶数时的情况
for(int i=1;i<=n;++i) printf("%d ",b[i]);//输出
return 0;
}