首页 > 其他分享 >Codeforces Round 894 (Div. 3) A-F题解

Codeforces Round 894 (Div. 3) A-F题解

时间：2023-08-25 15:57:09浏览次数：46  
标签：GIL 894 int 题解 sum cin Div include _##

A. Gift Carpet

题意

最近，特马和维卡庆祝了家庭日。他们的朋友 Arina 送给他们一块地毯，这块地毯可以用拉丁文小写字母的\(n \cdot m\)表来表示。

维卡还没看过礼物，但特马知道她喜欢什么样的地毯。如果维卡能在地毯上读出自己的名字，她一定会喜欢的。她从左到右逐列阅读，并从当前列中选择一个或零个字母。

从形式上看，如果可以从左到右依次选择四个不同的列，使第一列包含 "v"，第二列包含 "i"，第三列包含 "k"，第四列包含 "a"，那么女孩就会喜欢这块地毯。

帮助 Tema 提前了解 Vika 是否会喜欢 Arina 的礼物。

题解

将每列的字符找出，使用string保存，然后从左到右通过string.find()依次寻找vika。

代码

#include <algorithm>
#include <iostream>
#include <string>
#include <vector>
using namespace std;
#define SZ(x) (int)(x.size())
#define FOR(i,x,y) for (int i = (x),_##i = (y);i < _##i;i++)
#define FORD(i,x,y) for (int i = (x),_##i = (y);i > _##i;i--)
inline void GIL();
int main() {
    ios::sync_with_stdio(false);cin.tie(nullptr);
    int t = 1;
    cin >> t;
    FOR (id, 1, t + 1) { GIL(); }
    return 0;
}
inline void GIL() {
    int n, m;
    cin >> n >> m;
    vector<string> v(m, "");	// 用来存储列字符串，一共m列。
    int ans = 0;
    string t = "vika";
    FOR (i,0, n) {	// i:[0, n - 1]
        string s;
        cin >> s;
        FOR (j, 0, m) {	// j:[0, m - 1]
            v[j] += s[j];	// 第j个字符放入第j列中。
        }
    }
    int idx = 0;
    FOR (i, 0, m) {	// i:[0, m - 1]
        if (v[i].find(t[idx]) != v[i].npos) idx++;
        if (idx == 4) break;	// 由于字符串'vika'的最大下标为3,当idx为4时就退出。
    }
    cout << (idx == 4 ? "YES\n" : "NO\n");	// 判断是否依次全部找到。
}

B. Sequence Game

题意

特马和维卡正在玩下面的游戏。

首先，维卡想出一个长度为 \(m\)的正整数序列 \(a\)，并把它写在一张纸上。然后，她又换了一张纸，按照下面的规则写下序列 \(b\)：

  • 首先，她写下 \(a_1\)。
  • 然后，她只写下那些\(a_i\)（\(2 \le i \le m\)），使得\(a_{i - 1} \le a_i\)。这个序列的长度记为 \(n\)。

例如，从序列\(a=[4, 3, 2, 6, 3, 3]\)，维卡将得到序列\(b=[4, 6, 3]\)。

然后，她把写有序列\(b\)的纸片交给特马。他则尝试猜出序列 \(a\)。

特马认为在这样的游戏中获胜的可能性很小，但他仍然希望至少找到一个序列 \(a\)可能是维卡最初选择的。请帮助他并输出任何这样的序列。

注意，您输出的序列长度不应超过输入序列长度的两倍。

题解

首先\(b\)的第一个元素是\(a\)中的，然后对\(b\)中的其他元素：

  • 如果\(b_{i-1} \le b_i\)，那么将\(b_i\)放入\(a\)中。

    当前\(a\)的最后一个元素一定是\(b_{i-1}\)，那么将\(b_i\)放入\(a\)后，一定能从\(a\)中得到\(b_i\)，因为\(b_{i-1} \le b_i\)。

    例如：\(b=[2,3,4]\)

    按照上面的规则，可以得到\(a=[2,3,4]\)，而这个\(a\)是可以再推出\(b=[2,3,4]\)的。

  • 否则，即\(b_{i-1} > b_i\)，将两个\(b_i\)放入\(a\)中。

    两个\(b_i\)放入\(a\)后，\(a\)的后三个元素依次为\([b_{i-1},b_i,b_i]\)，由于\(b_{i-1} > b_i\)，满足\(a_{i-1} \le a_i\)的就只有\([b_i,b_i]\)，并得到一个\(b_i\)。

    例如：\(b=[3,2,1]\)

    按上面的规则，可以得到\(a=[3,2,2,1,1]\)，同样也可以再推出\(b=[3,2,1]\)的。

按上面的规则得到的\(a\)最长为\(2\times n - 1\)，小于\(2 \times n\)，满足要求。

代码

#include <algorithm>
#include <iostream>
#include <string>
#include <vector>
using namespace std;
#define SZ(x) (int)(x.size())
#define FOR(i,x,y) for (int i = (x),_##i = (y);i < _##i;i++)
#define FORD(i,x,y) for (int i = (x),_##i = (y);i > _##i;i--)
inline void GIL();
int main() {
    ios::sync_with_stdio(false);cin.tie(nullptr);
    int t = 1;
    cin >> t;
    FOR (id, 1, t + 1) { GIL(); }
    return 0;
}
inline void GIL() {
    int n;
    cin >> n;
    vector<int> v(n);	// 用来存放b数组
    FOR (i, 0, n) cin >> v[i];
    vector<int> ans;	// 用来存放a数组
    ans.push_back(v[0]);	// 首先b[0]一定在a中
    FOR (i, 1, n) {	// i:[1, n - 1]
        if (v[i] >= v[i - 1]) ans.push_back(v[i]);	// 只需要放一个
        else {	// 需要放两个
            ans.push_back(v[i]);
            ans.push_back(v[i]);
        }
    }
    cout << SZ(ans) << "\n";
    FOR (i, 0, SZ(ans)) {
        cout << ans[i] << " \n"[i == SZ(ans) - 1];
    }
}

C. Flower City Fence

题意

安雅住在花城。根据市长的命令，她必须为自己修建一道围墙。

围栏由 \(n\)块木板组成，每块木板高 \(a_i\)米。根据命令，木板的高度不得增加。换句话说，对于所有的\(i < j\)，一定满足\(a_i \ge a_j\)。

安雅开始好奇她的栅栏是否与对角线对称。换句话说，如果她按照相同的顺序水平铺设所有木板，是否会得到相同的栅栏。

例如，对于\(n = 5\)、\(a = [5, 4, 3, 2, 1]\)，栅栏是对称的。因为如果所有木板都横向铺设，栅栏将是\([5, 4, 3, 2, 1]\)，如图所示。

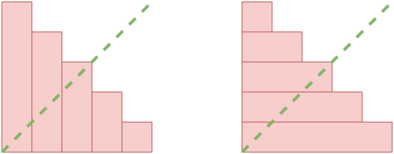
左边的栅栏是 \([5, 4, 3, 2, 1]\)，右边的栅栏同样是水平铺设的

但是对于\(n = 3\)、\(a = [4, 2, 1]\)，栅栏并不对称。因为如果所有的木板都横向铺设，栅栏将是\([3, 2, 1, 1]\)，如图所示。

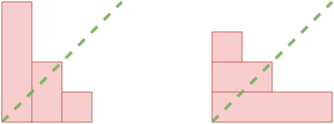
左边的栅栏是 \([4, 2, 1]\)，右边的栅栏同样是水平放置的

帮助安雅判断她的栅栏是否对称。

题解

我们可以进行模拟。先得到一列一列摆放好的木板，再尝试在现在摆放好的木板上一行一行地再次覆盖原来的木板。以上面的两张图片为例，将右边的图片放到左边的图片上，看右边的图片是否能与左边的图片完全重合。如果能，就是对称的；否则就不是对称的。

那如何实现模拟上诉过程呢？

设\(mi_i\)表示\([1,i]\)中\(a_i\)的最小值，由于\(a_i\)是非递增的，所以\(mi\)数组就是\(a\)数组。

我们尝试将右边的图片中的木板，从下往上，一个一个地平移到左边图片中。

那么对于右边的从下往上的第\(i\)个木板来说，其长度为\(a_i\)，将其平移到左边图片后，如果想完全重合，那么左边图片在下标从\(1\)到下标\(a_i\)的范围中，其最小值需要大于等于\(i\)。即需要满足\(a[a_i] \ge i\)。

这里\(a[a_i] \ge i\)，里面的\(a_i\)表示下标为\(a_i\)，而\(a[a_i]\)表示下标\(1\)到下标\(a_i\)的最小值\(mi[a_i]\)。

所以要满足对称，那么\(a_i\)就需要当a的下标，那么\(a_i\)就需要小于等于\(n\)。

#include <iostream>
#include <vector>
using namespace std;
#define FOR(i,x,y) for (int i = (x),_##i = (y);i < _##i;i++)
#define FORD(i,x,y) for (int i = (x),_##i = (y);i > _##i;i--)
inline void GIL();
int main() {
    ios::sync_with_stdio(false);cin.tie(nullptr);
    int t = 1;
    cin >> t;
    FOR (id, 1, t + 1) { GIL(); }
    return 0;
}
inline void GIL() {
    int n;
    cin >> n;
    vector<int> v(n + 1, 0);	// a数组
    bool ans = 1;	// 记录答案，1表示对称，0表示不对称。
    FOR (i, 1, n + 1) {
        cin >> v[i];
        if (v[i] > n) {	// a[i] > n，一定不满足对称。
            ans = 0;
        }
    }
    if (!ans) {
        cout << "NO\n";
        return;
    }
    FOR (i, 1, n + 1) {
        if (v[v[i]] < i) { // 平移，需要满足a[a[i]] >= i
            ans = 0;
            break;
        }
    }
    cout << (ans ? "YES\n" : "NO\n");
}

D. Ice Cream Balls

题意

特马决定提高自己制作冰淇淋的技能。他已经学会了如何恰好用两个球把冰淇淋做成圆锥形。

在痴迷冰淇淋之前，特马对数学很感兴趣。因此，他很想知道，要制作恰好 \(n\)种不同冰淇淋，最少需要多少个球。

有很多可能的冰淇淋口味：\(1, 2, 3, \dots\).特马可以用任何口味（可能相同）制作双球冰淇淋。

如果组成冰淇淋的两个球的味道的集合是不同的，则这两个冰淇淋被认为是不同的。例如，\(\{1, 2\} = \{2, 1\}\)，但是\(\{1, 1\} \neq \{1, 2\}\)。

例如，有以下冰淇淋球 \(\{1, 1, 2\}\)，特马只能做两种冰淇淋 \(\{1, 1\}\)和\(\{1, 2\}\)。

注意，特马不需要同时制作所有的甜筒冰淇淋。这意味着他可以独立制作冰淇淋甜筒。另外，为了在某个\(x\)的情况下制作出下面的甜筒\(\{x, x\}\)，特马至少需要\(x\)类型的\(2\)个球。

请帮助特马回答这个问题。可以证明答案总是存在的。

题解

对于不同口味的\(x\)个球来说，可以构成\(C_x^2\)种不同的冰淇淋。那么我们可以二分得到最小的\(x\)，使得\(C_x^2 \ge n\)。我们想得到恰好n种冰淇淋的话，对于\(C_{x-1}^2\)多的部分\(left=n-C_{x-1}^2\)，我们可以添加与\(x\)个球味道相同的球，使得恰好能组成\(n\)种不同的冰淇淋。

代码

#include <algorithm>
#include <iostream>
using namespace std;
using ll = long long;
using i128 = __int128_t;
#define FOR(i,x,y) for (int i = (x),_##i = (y);i < _##i;i++)
#define FORD(i,x,y) for (int i = (x),_##i = (y);i > _##i;i--)
inline void GIL();
int main() {
    ios::sync_with_stdio(false);cin.tie(nullptr);
    int t = 1;
    cin >> t;
    FOR (id, 1, t + 1) { GIL(); }
    return 0;
}
inline void GIL() {
    ll n;
    cin >> n;
    ll l = 2, r = 1e18;
    auto check = [&] (ll mid) {
        i128 t = mid;	// 防爆longlong
        return (t * (t - 1) / 2 >= n);	// C_{t}^2 >= n
    };
    while (l < r) {	// 二分得到x，使得C_x^2 >= n
        ll mid = (l + r) >> 1;
        if (check(mid)) r = mid;
        else l = mid + 1;
    }
    ll all = l * (l - 1) / 2;	// 计算C_X^2
    if (all > n) {
        all = n - (l - 1) * (l - 2) / 2;	// left = n - C_{x-1}^2
        l += all - 1;	// 这个-1是为了得到答案，按我的想法，应该是加all。
    }
    cout << l << "\n";
}

E. Kolya and Movie Theatre

题意

最近，科里亚发现他所在的城市即将开一家新的电影院，每天都会放映一部新电影，连续放映\(n\)天。因此，在数字\(1 \le i \le n\)的那一天，电影院将首映\(i\)部电影。此外，科里亚还找出了电影的排片表，并为每部电影分配了娱乐价值，用\(a_i\)表示。

然而，Kolya 没有去电影院看电影的时间越长，下一部电影的娱乐价值的下降幅度就越大。这种下降相当于\(d \cdot cnt\)，其中\(d\)是一个预定值，\(cnt\)是距离上次去电影院的天数。我们还知道，科里亚设法在新电影院开业前一天去了另一家电影院，这一天的数字是\(0\)。因此，如果我们在数字\(i\)的那一天第一次去电影院，那么\(cnt\)------等于距离上次去电影院的天数\(i\)。

例如，如果\(d = 2\)和\(a = [3, 2, 5, 4, 6]\)，那么通过观看指数为\(1\)和\(3\)的电影 \(1\)这一天的\(cnt\)值等于\(1 - 0 = 1\)，\(3\)这一天的\(cnt\)值等于\(3 - 1 = 2\)，所以电影的总娱乐值为\(a_1 - d \cdot 1 + a_3 - d \cdot 2 = 3 - 2 \cdot 1 + 5 - 2 \cdot 2 = 2\)。

不幸的是，科里亚只有时间去看最多 \(m\)部电影。帮助他制定一个参观电影院的计划，使他参观的所有电影的总娱乐价值最大化。

题解

我们可以发现，假设最后一部电影是在\(x\)天看的，那么不管前面看了多少部电影，值\(d\)对总娱乐值的贡献为\(x \times d\)。也就是说，是否选择看电影对\(x \times d\)无影响。

那么我们可以贪心，遍历天数，对于每一天\(i\)，都假设这是看电影的最后一天，在这\(i\)部电影中，最多选择\(m\)部电影，其娱乐值的和为\(sum\)，那么这时候的最大总娱乐值为\(sum - i \times d\)。

那么，我们想让最大娱乐值最大，那么\(sum\)就需要最大，那么我们就需要娱乐值最大的\(m\)部电影，并且所有娱乐值都大于0。考虑使用最小堆来维护最大的\(m\)个娱乐值以及\(sum\)。

代码

#include <algorithm>
#include <iostream>
#include <queue>
#include <utility>
#include <vector>
using namespace std;
using ll = long long;
#define FOR(i,x,y) for (int i = (x),_##i = (y);i < _##i;i++)
#define FORD(i,x,y) for (int i = (x),_##i = (y);i > _##i;i--)
inline void GIL();
int main() {
    ios::sync_with_stdio(false);cin.tie(nullptr);
    int t = 1;
    cin >> t;
    FOR (id, 1, t + 1) { GIL(); }
    return 0;
}
struct cmp {
    bool operator () (int &a, int & b) {
        return b < a;	// 用来确保最小值在堆顶部。
    }
};
inline void GIL() {
    int n, m;
    ll d;
    cin >> n >> m >> d;
    vector<ll> v(n);
    priority_queue<int, vector<int>, cmp> pq;	// 最小堆
    ll ans = 0, sum = 0;	// 最后的答案ans，还有sum
    FOR (i, 0, n) {	// i:[0,n-1]
        cin>> v[i];
        if (v[i] <= 0) continue;	// 忽略小于0的值
        if (pq.empty() || SZ(pq) < m) {	// 如果还不够m部电影，就一直看
            sum += v[i];
            pq.push(v[i]);
        } else if (SZ(pq) == m && v[i] > pq.top()) {	// 已经看了m部电影，那么可以去掉最小的值，放入较大的值
            sum += v[i] - pq.top();
            pq.pop();	// 去掉最小的
            pq.push(v[i]);	// 放入比较大的
        }
        ans = max(ans, sum - (i + 1) * d);	// 更新一下答案。
    }
    cout << ans << "\n";
}

F. Magic Will Save the World

题意

黑暗力量的传送门在两个世界的交界处打开了，现在整个世界都面临着可怕的威胁。为了关闭传送门，拯救世界，你需要打败一个又一个从传送门中出现的\(n\)怪物。

只有女魔法师维卡才能胜任。她拥有两种魔法能力--水魔法和火魔法。在一秒钟内，维卡可以产生 \(w\)个单位的水系法力和 \(f\)个单位的火系法力。她需要法力值来施法。最初维卡有\(0\)个单位的水系法力值和\(0\)个单位的火系法力值。

每个从传送门中出现的\(n\)个怪物都有自己的力量，用正整数表示。要打败强度为\(s_i\)的第\(i\)个怪物，维卡需要施放至少相同强度的水系法术或火系法术。换句话说，维卡可以在水系法术上花费至少 \(s_i\)个单位的水系法力，或者在火系法术上花费至少 \(s_i\)个单位的火系法力。

维卡可以瞬间创造和施放法术。只要有足够的法力，维卡每秒可以施放无限多个法术。

女巫想要尽快拯救世界，请告诉她需要多少时间。

题解

由于要求最小时间，表示可以二分找到这个最小时间。

那么，对于一个时间\(mid\)，我们如何确定是否能在\(mid\)秒内打败所有怪物呢？

首先，我们拥有两种法术，那么，对于一种法术而言，其值为\(val\)，我们想最大程度地使用这种法术，所以我们需要在\(n\)种怪物的数值中，找到和\(sum\)最接近\(val\)的值。而这个，可以通过0/1背包实现，背包总容量为\(val\)，每种怪物\(i\)相当于容量为\(s_i\)，价值为\(s_i\)的物品。求出此时的最大价值即为\(sum\)。

然后再判断另一种法术是否能打败剩下的怪物即可。

代码

#include <algorithm>
#include <iostream>
#include <vector>
using namespace std;
using ll = long long;
#define SZ(x) (int)(x.size())
#define FOR(i,x,y) for (int i = (x),_##i = (y);i < _##i;i++)
#define FORD(i,x,y) for (int i = (x),_##i = (y);i > _##i;i--)
inline void GIL();
int main() {
    ios::sync_with_stdio(false);cin.tie(nullptr);
    int t = 1;
    cin >> t;
    FOR (id, 1, t + 1) { GIL(); }
    return 0;
}
inline void GIL() {
    ll w, f;
    cin >> w >> f;
    int n;
    cin >> n;
    ll sum =0;
    vector<int> v(n);
    FOR (i, 0, n) {
        cin >> v[i];
        sum += v[i];	// 所有怪物的总和为sum
    }
    ll mx = max(w, f);
    ll l = 1, r = (sum + mx - 1) / mx;	// 二分边界，只使用一种法术消灭怪物时的最小时间。
    auto check = [&] (ll mid) {
        ll sum_w = mid * w, sum_f = mid * f;
        ll ALL = min(sum_w, sum_f);	// 采取最小的法术作为背包容量。
        vector<int> dp(ALL + 1, 0);	// 容量为ALL的背包
        FOR (i, 0, n) {
            FORD (j, ALL, v[i] - 1) {
                dp[j] = max(dp[j], dp[j - v[i]] + v[i]);	// 0/1背包
            }
        }
        return max(sum_f, sum_w) >= sum - dp[ALL];	// 看另一种法术是否能消灭剩下的怪物。
    };
    while (l < r) {	// 二分时间。
        ll mid = (l + r) >> 1;
        if (check(mid)) r = mid;
        else l = mid + 1;
    }
    cout << l << "\n";
}

标签：GIL,894,int,题解,sum,cin,Div,include,_##
From： https://www.cnblogs.com/FanWQ/p/17657139.html

相关文章

  • arc142,arc143,arc144题解
    ARC142A-EAReverseandMinimize憨的。BUnbalancedSquares构造。考虑一行之内大小交错，行间则单调排列。这样可以使得每个点上下大小关系抵消，左右的又保持一样，于是就合法了。CTreeQueries处在\(1,2\)最短路径上的点一定到两个点距离和最小，于是找到这个距离。但是这个......
  • 网络规划设计师真题解析--IP地址类（一）
    将地址块192.168.0.0/24按照可变长子网掩码的思想进行子网划分，若各部门可用主机地址需求如下表所示，则共有(27)种划分方案，部门3的掩码长度为(28)。（2018年）（27）A.4B.8C.16D.32（28）A.25B.26C.27D.28部门所需地址总数部门1100部门250部门316部门410部门58答案：（27）C（28）C解析：（27）部门所......
  • RTSP流媒体服务器EasyNVR视频平台设备通道时间与服务器录像时间不一致的问题解决步骤
    EasyNVR平台优秀的视频能力在于通过RTSP/ONVIF协议，将前端接入设备的音视频资源进行采集，并转码成适合全平台、全终端分发的视频流格式，包括RTMP、RTSP、FLV、HLS、WebRTC等格式。平台已经在智慧水利、智慧工厂、智慧校园、智慧仓储等场景中应用。​ 有用户反馈，设......
  • CF258D Little Elephant and Broken Sorting 题解
    题意给定一个长度为\(n\)的排列\(a\)和\(m\)个形如\(\left(x,y\right)\)的操作，每次操作有\(50\%\)的概率交换\(a_x,a_y\)，求最终排列的期望逆序对数。（\(1\len,m\le5000\)）。题解首先转化答案\[\text{Ans}=\sum\limits_{i=1}^{n}\sum\limits_{j=i+1}^{......
  • ADRABR - Adrita and Her Bike Ride 题解
    1.题目大意题目传送门2.思路因为每条道路长均为\(1km\)，所以我们可以在建边时就加上走这条路的初始成本，即对于每条边的两端\(a,b\)和通行费\(w\)，我们直接\(add(a,b,w+12)\)即可。再就是由于是多组数据，所以我们在每次输入前要清空数组，然后跑一遍最短路模板即可。3.代码#......
  • java.lang.NoClassDefFoundError问题解决方案
    骑士李四记录：场景在pom.xml中引入一个包，之后启动部署项目，出现java.lang.NoClassDefFoundError的问题。报错信息：解决方案：加入这段代码<plugin><groupId>org.apache.maven.plugins</groupId><artifactId>maven-dependency-plugin</artifactId><executi......
  • 国标视频平台EasyGBS视频能力平台Linux版内核启动报错端口占用的问题解决方案
    EasyGBS国标视频云服务是基于国标GB/T28181协议的视频能力平台，可实现的视频功能包括：实时监控直播、录像、检索与回看、语音对讲、云存储、告警、平台级联等功能。平台部署简单、可拓展性强，支持将接入的视频流进行全终端、全平台分发，分发的视频流包括RTSP、RTMP、FLV、HLS、WebRTC等......
  • centos8无法安装问题解决
    1、centos使用yum或者dnf命令安装都失败，且连接互联网正常，如下图所示：2、可查看/var/log/dnf.log日志3、备份yum源，重新下载华为centos8版本软件仓库mv/etc/yum.repos.d/Centos*bak/curl-o/etc/yum.repos.d/CentOS-Base.repohttps://repo.huaweicloud.com/repository/conf/......
  • [AGC007D] Shik and Game 题解
    一道有意思的\(\text{dp}\)呀。思路我们容易发现，一个点最多会往回走一次。也就是每一个点最多被遍历三次。因此，我们可以考虑每个点的贡献。\[dp_i=\min_{j=1}^{i-1}dp_j+x_i-x_j+\max(2\times(x_i-x_{j+1}),T)\]其中，\(dp_i\)表示前\(i\)个金币全部取完，此时位于第\(i\)......
  • 『题解』JOISC2022B 京都観光 (Sightseeing in Kyoto)
    AtCoder题目链接Luogu题目链接观察题目，不自觉地想到了dp，但是再一看\(\text{1e5}\)数据范围，意识到大概是\(2^{\text{1e5}}\)的复杂度，绝望了……然后就很自然地想到了最优策略。（思路很巧妙但是我当时没想到。）考虑有三行（或三列），分别记为\(i,j,k\)，如果\(j>i\landj>......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99