题目大意
给定 \(n,p\),求:
\[\left(\sum_{i=1}^n\sum_{j=1}^n\gcd(i,j)^{i+j}\right)\bmod p \]多组数据。
思路分析
老规矩,先化式子:
\[\begin{aligned} \sum_{i=1}^n\sum_{j=1}^n\gcd(i,j)^{i+j}&= \sum_{d=1}^n\sum_{i=1}^n\sum_{j=1}^nd^{\,i+j}\,[\gcd(i,j)=d]\\ &=\sum_{d=1}^n\sum_{i=1}^{\left\lfloor\frac{n}{d}\right\rfloor}\sum_{j=1}^{\left\lfloor\frac{n}{d}\right\rfloor}d^{\,(i+j)\,d}\,[\gcd(i,j)=1]\\ &=\sum_{d=1}^n\sum_{x=1}^{\left\lfloor\frac{n}{d}\right\rfloor}\mu(x)\sum_{i=1}^{\left\lfloor\frac{n}{xd}\right\rfloor}\sum_{j=1}^{\left\lfloor\frac{n}{xd}\right\rfloor}d^{\,(i+j)\,xd} \end{aligned}\]观察后面的部分:
\[\begin{aligned} \sum_{i=1}^{\left\lfloor\frac{n}{xd}\right\rfloor}\sum_{j=1}^{\left\lfloor\frac{n}{xd}\right\rfloor}d^{\,(i+j)\,xd}&= \Bigg(\sum_{i=1}^{\left\lfloor\frac{n}{xd}\right\rfloor}d^{\,ixd}\Bigg)\times \Bigg(\sum_{j=1}^{\left\lfloor\frac{n}{xd}\right\rfloor}d^{\,jxd}\Bigg)\\ &=\Bigg(\sum_{i=1}^{\left\lfloor\frac{n}{xd}\right\rfloor}d^{\,ixd}\Bigg)^2 \end{aligned}\]设 \(f(d,n)=\sum\limits_{i=1}^nd^{\,i}\),那么后面的部分就可以表示为 \(f^2(d^{xd},\left\lfloor\frac{n}{xd}\right\rfloor)\)。
我们发现,\(f\) 是一个首项为 \(d\),公比为 \(d\) 的等比数列前 \(n\) 项和,可以 \(O(\log n)\) 计算,具体的说:
\[f(d,n)=\begin{cases}d^{\,n}+f(d,\dfrac{n-1}{2})&n\equiv 1\pmod 2\\(d^{\frac{n}{2}}+1)\times f(d,\dfrac{n}{2})&n\equiv 0\pmod 2\end{cases} \]那么我们的式子就变成了:
\[\sum_{d=1}^n\sum_{x=1}^{\left\lfloor\frac{n}{d}\right\rfloor}\mu(x)f^2(d^{xd},\left\lfloor\frac{n}{xd}\right\rfloor) \]我们发现,如果暴力计算这个式子,也就是暴力枚举 \(d\),枚举 \(x\),直接计算 \(f\),那么时间复杂度是 \(O(n\log n)\) 的,可以通过(需要轻微卡常)。
- 为什么时间复杂度是 \(O(n\log n)\)?
证明就不证了(其实是我不会),这里放一张图:
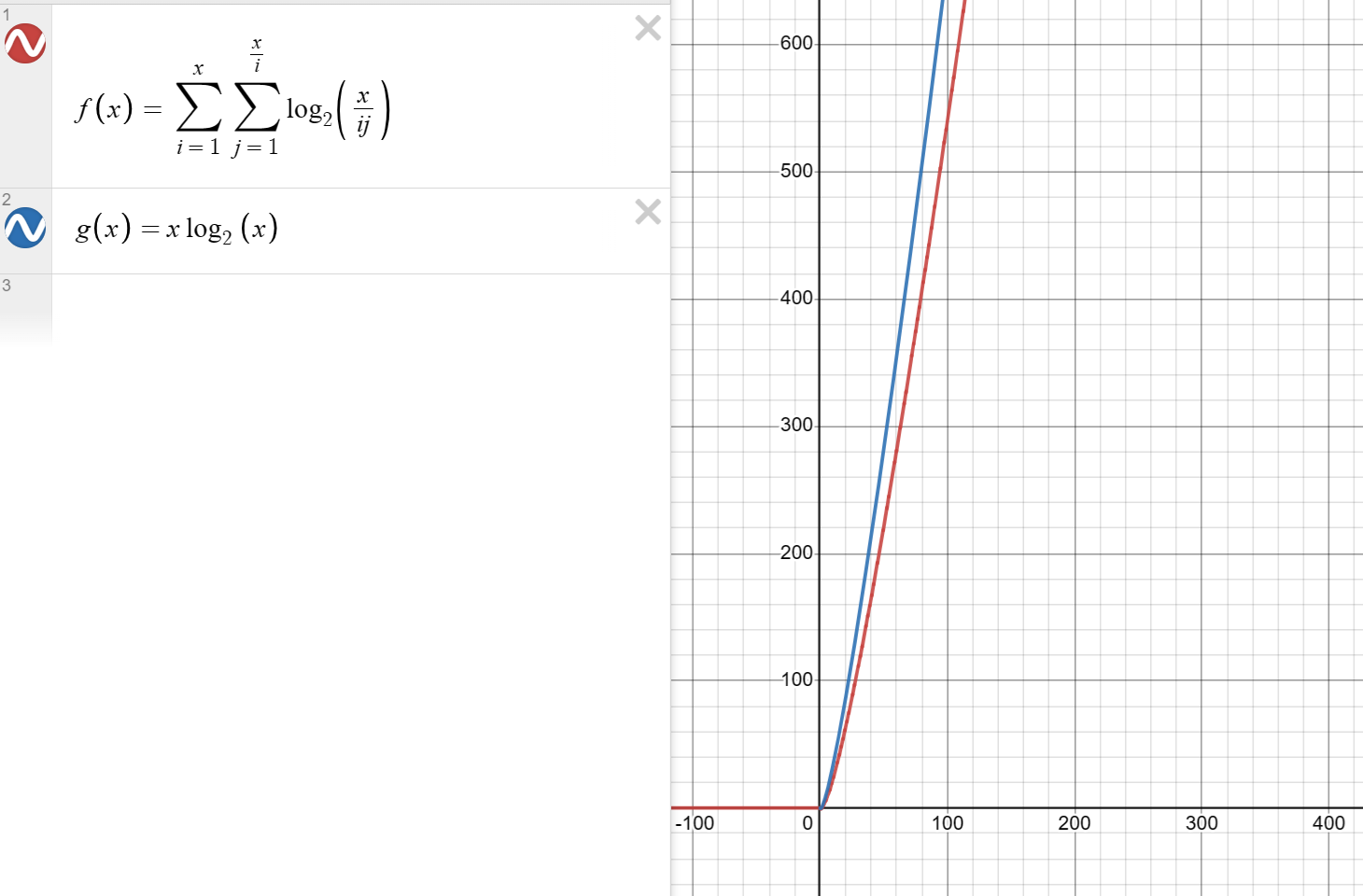
代码
#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cmath>
using namespace std;
const int N=1550000,L=1500000;
#define int long long
int prime[N],mu[N],v[N];
int cnt,n,T,mod;
int mode(int x){
while(x>mod) x-=mod;
return x;
}
int q_pow(int a,int b){
int res=1;
while(b){
if(b&1) res=(res*a)%mod;
a=(a*a)%mod;
b>>=1;
}
return res;
}
void sieve(){
mu[1]=1;
for(int i=2;i<=L;i++){
if(!v[i]){prime[++cnt]=i;mu[i]=-1;}
for(int j=1;j<=cnt&&i*prime[j]<=L;j++){
v[i*prime[j]]=1;
if(i%prime[j]==0) break;
mu[i*prime[j]]=-mu[i];
}
}
}
int f(int d,int n){
if(n==1) return d;
int res=f(d,n>>1);
res=mode(res+res*q_pow(d,n>>1)%mod);
if(n&1) res=mode(res+q_pow(d,n)%mod);
return res;
}
signed main(){
sieve();
scanf("%lld",&T);
while(T--){
scanf("%lld%lld",&n,&mod);
int res=0;
for(int d=1;d<=n;d++){
int r=n/d;
for(int x=1;x<=r;x++){
if(!mu[x]) continue;
int ans=f(q_pow(d,x*d%(mod-1)),r/x);
res=mode(res+mu[x]*ans*ans%mod+mod);
}
}
cout<<res<<'\n';
}
return 0;
}