Lecture 1
课程介绍:
(1) 图同构的群论算法。
(2) 匹配的代数算法。
前置知识:群论,包括群同态、合成列、群作用、自同构等。
定义 一张图 \(G = (V, E)\),\(V\):点集,\(E \subset \binom V2\):边集。其中 \(\binom V2\) 表示从 \(V\) 中选出两者构成的集族。\(|V|\) 是 \(G\) 的 order,\(|E|\) 是 \(G\) 的 size。
定义 生成子图 \(G' = (V, E'), E' \subseteq E\),导出子图 \(G' = (U, E'), U \subseteq V, E' = \{\{i, j\} \mid i, j \in U, \{i, j\} \in E\}\)。\(G\) 是二分图如果 \(\exists V = L \uplus R\),使得 \(\forall e \in E, e = \{l, r\}, l \in L, r \in R\)。其中 \(\uplus\) 表示不交并。\(G\) 不连通如果 \(\exists V = L \uplus R, \forall e \in E, e \subseteq L\) or \(e \subseteq R\)。
定义 \(M \subseteq E\) 是一个匹配,如果 \(\forall v \in V\),\(\exists\) 至多一个 \(e \in M\),使得 \(v \in e\)。\(M\) 是一个完美匹配,如果把至多改为恰好。
定义 \(G = (L \uplus R, E)\),对 \(S \subseteq L, N(S) = \{u \in R \mid \exists v \in S, \{u, v\} \in E\}\),\(S\) 是 \(L\) 的一个 shrunk subset,如果 \(|S| > |N(S)|\)。
定理 (Hall) \(G\) 拥有完美匹配当且仅当 \(G\) 没有 shrunk subset。
定义 \(G = (V, E)\),对 \(S \subseteq L\),令 \(o(S)\) 为删掉 \(S\) 与其相邻边后的图 \(G[V\setminus S]\) 的奇数大小连通块的个数。\(S\) 是 \(L\) 的一个 obstruction,如果 \(|o(S)| > |S|\)。
定理 (Tutte) \(G\) 拥有完美匹配当且仅当 \(G\) 没有 obstruction。
上面两个定理说明了完美匹配问题 \(\in \text{NP} \cap \text{co-NP}\),当然,我们知道,完美匹配 \(\in \text P\)。比如在二分图上的增广路(或称匈牙利)算法。下面介绍一种代数做法。这种做法在过程上更简洁,且可并行化。
定义 \(A = (a_{ij}) \in M(n, \mathbb Q)\),即 \(A\) 是一个在 \(Q\) 上的 \(n\) 阶方阵。\(\det(A) = \sum\limits_{\sigma \in S_n} \text{sgn}(\sigma)\prod_{i=1}^n a_{i, \sigma(i)}\)。
定理 (Lovász) 令 \(X_G = \begin{cases}x_{ij} & \{i, j'\} \in E \\ 0 & \text{otherwise}\end{cases}\)。则 \(G\) 有完美匹配当且仅当 \(\det(X_G) \neq 0\)。
其中 \(x_{ij}\) 为互相独立的不定元。也就是说,\(\det(X_G)\) 是一个(不超过) \(|E|\) 元 \(|V|\) 次多项式,\(\in \mathbb Q[x_{ij}]\)。
证明按照行列式的定义是显然的,但是这相当于把所有问题甩给了如何测试 \(\det(X_G) \neq 0\),直接展开会有指数多项。
我们可以很快想到一个随机做法。关键点在于一个 \(d\) 阶多项式 \(f\) 的零点只有至多 \(d\) 个。
引理 (Schwartz-Zippel) \(f\in \mathbb F[y_1, y_2, \ldots, y_m]\) 是一个 \(d\) 阶多项式,那么 \(\text{Pr}_{a_1, a_2, \ldots, a_m \in [2d]^m}(f(a_1, a_2, \ldots, a_m) = 0) \leq \frac 12\)。其中 \(\mathbb F[y_1, y_2, \ldots, y_m]\) 表示在数域 \(\mathbb F\) 上的 \(m\) 元多项式,\([2d]\) 表示 \(\{1, 2, \ldots, 2d\}\)。
而行列式是可以高效并行计算的(高斯消元无法做到这一点)。详见 Lecture 5。
更一般地,我们关心如下问题(symbolic determinant identity testing, SDIT)
Input:给定不定元 \(x_1, \ldots, x_m\) 和一个矩阵 \(X\),使得 \(X_{ij} = x_k\) or \(a \in \mathbb Q\)。
Output:是否有 \(\det(X) = 0\)?
我们有以下结果:(a) SDIT 有高效的多项式时间随机做法(Schwartz-Zippel)。(b) SDIT \(\in \text P\) 则 algebraic version of \(\text P \neq \text {NP}\)。
SDIT 的更多问题详见 Lecture 7。
定义 \(G = (V, E)\) 和 \(H = (W, F)\) 同构,如果存在一个双射 \(f:V \in W\) 使得 \(\{v, v'\} \in E\) 当且仅当 \(\{f(v), f(v')\} \in F\)。图同构(GI)问题即判断两张图是否同构。
定理 \(GI \in \text{NP} \cap \text{co-AM}\),\(GNI \in \text{AM}\)。
在之前,GI 最好的算法是 \(2^{\sqrt n} = \exp(\tilde O(n))\),其中 \(\tilde O(n)\) 表示 \(\{n\log^c n\}\)。
定理 (Babai, 2015) GI 可在 \(\exp(O(\log^3 n))\) 解决。
有两种切入 GI 的技巧:组合(combinatorial)和群论(group-theoretic)。
组合的做法是,考虑从一对对应点开始染色,其他点暂时无色。之后每次把一个点变成它周围点的 multiset,然后为每一种不同的 multiset 分配一个颜色作为下一轮的颜色。这样做上若干轮后,到所有颜色的类都固定了,我们也就找到了一个同构(或在中途发现无法同构)。这个过程叫做 Weisfeiler-Leman 过程。
定理 (Cai-Fürer-Immerman) 存在一对不同构的图,无法在 \(k\) 轮内被区分,而 \(k = O(n)\)。甚至可以是一对三度图,即所有点度数均为 \(3\) 的图。
所以组合方法是行不通的。接下来我们介绍三度图上的群论做法。
定理 (Luks) 对两个三度图 \(G, H\),存在多项式时间的同构测试算法。
Lecture 2
我们接下来证明上述定理。实际上,我们会发现,对于度数不超过一个常数的图,这个做法均有效。
首先我们来看看群论是如何应用到图同构问题上的。
定义 \(G = (V, E)\),其自同构集合 \(\text{Aut}(G) = \{f:V \to V \mid {v, v'} \in E \Leftrightarrow \{f(v), f(v')\} \in E\}\)。
很显然地,\(\text{Aut}(G)\) 是一个群。而 \(\text{Iso}(G, H)\) 不是群而是 \(\text{Aut}(G)\) 的一个陪集。
接下来的一个问题是,对 \(n\) 个点的图,其对称群的一个子群 \(S \leq \text{Sym}(V)\) 的大小是指数级的,该如何存储它?答案是存储其生成元。
定理 对 \(T \subseteq P\),\(\exists T\) 使得 \(\langle T \rangle = P, |T| \leq \lceil \log_2 |P|\rceil\)。
证明是显然的,考虑 \(T_0 = \{1\}\),每次随便加入一个在 \(P\) 而不在 \(\langle T_i \rangle\) 里的元素,得到 \(T_{i+1}\),根据 Lagrange 定理可知 \([\langle T_{i+1}\rangle, \langle T_i \rangle] \geq 2\),因此至多只需要 \(\log_2 |P|\) 次包含整个 \(P\)。
因此,今后提到的所有的关于某个对称群的子群的问题,我们全部用其生成元进行存储、运算。
如何把图同构问题归约到图自同构问题?后者有更好的代数性质。
这是简单的。考虑如果 \(G, H\) 都是连通的,那么构造一个大图把两者全部包含,找到这个大图的自同构群,然后仅把那些交换了 \(G, H\) 位置的生成元留住。如果不连通,根据同构关系的传递性,对 \(G\) 的每一个连通块枚举 \(H\) 的连通块,如果找到同构的连通块,就把两者划掉,继续剩下的部分。
于是我们的任务便是图自同构问题。这个问题现在可以基于一个置换群算法的框架。
给定一个 \(P \leq \text{Sym}(U)\) 的生成集合,我们有如下问题
- Membership: 给定 \(\sigma \in \text{Sym}(U)\),是否有 \(\sigma \in P\)?
- Order:计算 \(|P|\)。
- Point Stabilizer: 对 \(v \in U\),计算 \(P_v = \{\sigma \in P \mid \sigma(v) = v\}\)。
- Set Stabilizer: 对 \(W \subseteq U\),计算 \(P_W = \{\sigma \in P \mid \sigma(W) = W\}\)。
Membership 是可以归约到 Order 的。因为可以通过把 \(\sigma\) 放到生成集合里看 order 有没有变大。
其中,Membership, Order, Point Stabilizer 是简单的,详见 Lecture 4。Set Stabilizer 是难的,Luks 说明了当 \(|P|=p^k\),其中 \(p\) 是质数,是简单的。
图自同构问题可以归约到 Set Stabilizer 上。考虑对于 \(G = (V, E)\),\(U = \binom V2\),\(P = \langle \sigma_{i, j} \mid \forall k, (i, k) \leftrightarrow (j, k)\rangle\),即交换点 \(i, j\) 时,与其相关的所有边交换。那么 \(P_E\) 便是 \(\text{Aut}(G)\)。
接下来我们证明三度图的同构问题可以归约到三度图的自同构问题,且 \(\text{Aut}\) 是一个 2-group,即大小为 \(2^l\) 的群,并在 Lecture 3 中说明为什么在这样的群下是好做的。
考虑枚举一对边 \(e = \{a, b\} \in G, e' = \{a', b'\} \in H\),建立两个新点 \(v, v'\),连接 \((v, a), (v, b), (v, v'), (v', a'), (v', b')\)。令 \(f = (v, v')\)。这样新图还是一个三度图,且 \(\text{Aut}\) 中保留了 \(f\),即 \(\text{Aut}_f\) 中,交换了 \(v, v'\) 的所有元素便是 \(\text{Iso}_{e \leftrightarrow e'}(G, H)\)。那么 \(\text{Iso}(G, H) = \bigcup_{e'} \text{Iso}_{e \leftrightarrow e'}(G, H)\)。
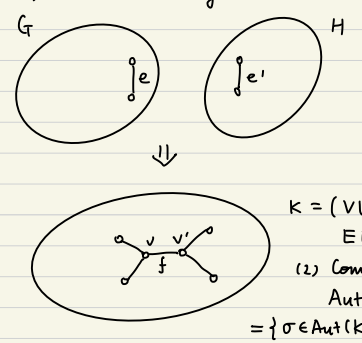
命题 (Tutte) \(|\text{Aut}(G)_f| = 2^l\)。
证明 既然已经有了一个固定物 \(f\),考虑数学归纳法。
定义 \(G_1 = (\{v, v'\}, f)\),\(G_{i+1}\) 为 \(G_i\) 加上相邻边与相邻点构成的图。则 \(\text{Aut}(G_1)_f = 2\)。若 \(\text{Aut}(G_i) = 2^j\) 已成立,考虑 \(\text{Aut}(G_{i+1})\)。令
\[\begin{aligned}\pi_i: \text{Aut}(G_{i+1})_f &\to \text{Aut}(G_i)_f \\ \alpha &\to \alpha|_{V(G_i)}\end{aligned} \]即把 \(\alpha\) 限制在 \(V(G_i)\) 上得到的更小的映射。那么 \(\pi_i\) 是一个群同态。所以 \(|\text{Aut}(G_{i+1})_f| = |\text{Im}(\pi_i)| |\text{Ker}(\pi_i)|\),根据归纳假设,\(\text{Im}(\pi_i)\) 只能是 2-group,接下来考虑 \(\text{Ker}(\pi_i)\),也就是那些把 \(G_i\) 不变的映射。这些映射只会改变 \(V(G_{i+1}) \setminus V(G_i)\),如果两个这里的点拥有相同的在 \(V(G_i)\) 中的邻居,那么这两个点可以互换。而 \(V(G_{i+1})\) 内的连边是在 \(G_{i+2}\) 里考虑的,所以现在不用在乎。那么如果有大于两个在 \(V(G_i)\) 中拥有相同的邻居,那么由于每个点度数只有三,这些邻居不可能还能提前在 \(G_i\) 中。所以能互换的只是许多对点。所以 \(\text{Ker}(\pi_i) \cong \mathbb Z_2^k, |\text{Ker}(\pi_i)| = 2^k\)。
接下来,我们利用这个过程算出 \(\text{Aut}(G)_f\)。
由于我们的群同态是一个 restrict,所以可知 \(\text{Im}(\pi_i)\text{Ker}(\pi_i) = \text{Aut}(G_{i+1})_f\)。其中 \(GH = \{gh \mid g \in G, h \in H\}\)。换句话说,两部分独立(熟悉群论的读者可知在一般的商群中这一点并不成立)。如果我们能够求出 \(\text{Im}(\pi_i), \text{Ker}(\pi_i)\) 的一组生成元,那么 \(\text{Aut}\) 的生成元可以通过 \(\bigcup_{g \in G} gH\) 得到。有关陪集的并的讨论详见 Lecture 3。
我们已经充分讨论了 \(\text{Ker}(\pi_i)\) 的结构,可知其是(在同构的意义上)若干个 \(\mathbb Z_2\) 组成的。
接下来我们考虑 \(\text{Im}(\pi_i)\)。并不是所有 \(\text{Aut}(G_i)_f\) 的元素都可以对应到一个或一些 \(\text{Aut}(G_{i+1})_f\) 中的元素。这是因为我们并没有考虑 \(E(G_{i+1}) \setminus E(G_i)\) 所造成的额外限制。考虑令 \(A = V(G_i) \cup \binom {V(G_i)}2 \cup \binom {V(G_i)}3\),即 \(G_i\) 的一二三元集合,
\[\begin{aligned}N: V(G_{i+1}) \setminus V(G_i) &\to A \\ v &\to \text{neighbors of }v \text{ in }G_i\end{aligned} \]考虑
\[\begin{aligned} A_1 &= \{a \in A \mid \exists ! v \in V(G_{i+1}) \setminus V(G_i), N(v) = a\} \\ A_2 &= \{a \in A \mid \exists u, v \in V(G_{i+1}) \setminus V(G_i), N(u) = N(v) = a\} \\ A' &= \{\{u, v\} \mid \{u, v\} \in E(G_{i+1})\} \end{aligned}\]其中 \(\exists !\) 表示存在唯一。
那么 \(\sigma \in \text{Aut}(G_i)_f\) 应该稳定化 \(A_1, A_2, A'\)。即 \(\sigma(A_1) = A_1, \sigma(A_2) = A_2, \sigma(A') = A'\)。
也就是说,当我们考虑 \(\text{Im}(\pi_i)\) 的时候,\(V(G_{i+1}) \setminus V(G_i)\) 变成了无标号的。我们需要考虑的仅有边的个数关系。
所以,我们的问题变为了,给定一个群 \(P \leq \text{Sym}(A)\),\(A\) 中每个点有一个颜色。我们需要计算 \(P' \leq P\),使得 \(P'\) 保颜色。
由于 \(A'\) 和 \(A_1, A_2\) 是两种不同的对 \(A\) 的划分,所以我们得到了 \(A\) 的如下划分
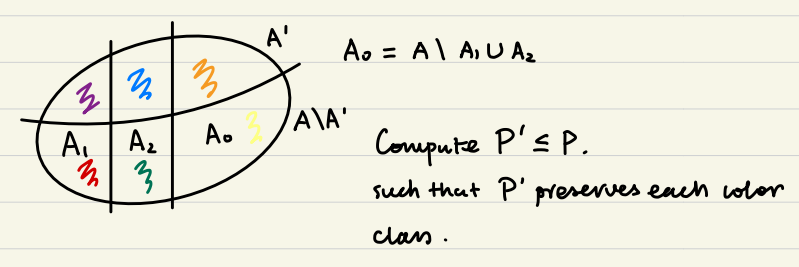
(实际上绿色是空集)
定义 有色集合自同构问题 (colored set automorphism)
Input: \(P \leq \text{Sym}(A)\) 的生成集合,\(A\) 是一个有色的集合。
Output: \(\{\sigma \in P \mid \sigma \text{ preserves colors}\}\) 的生成集合。
在这里,我们还有特殊性质 \(P\) 是一个 2-group。
Exercises for Lectures 1 and 2
Lecture 3
我们再来重新描述一遍现在的问题。令 \(P \leq \text{Sym}(A)\) 是一个 2-group,\(A = A_1 \uplus A_2 \uplus \ldots \uplus A_c\),计算 \(Q = \{\sigma \in P \mid \sigma(A_i) = A_i\}\)。\(P, Q\) 都以生成集合的方式存在。
我们知道,\(p\)-group 的一个重要性质就是 Sylow's theorem。
定理 (Sylow) 若 \(|G| = p^l \cdot s\),\(p \not| s\),则 \(G\) 存在阶数为 \(p^i\)(\(1 \leq i \leq l\))的子群。
这说明 \(G\) 有着平缓的子结构。我们尝试用递归来解决问题。
一个观察是,如果 \(P\) 不 transitive,我们可以对每个轨道单独解决。
定义 \(P \leq \text{Sym}(A), B \subseteq A\),称 \(B\) 在 \(P\) 是稳定的,如果 \(\forall b \in B, \sigma \in P\) 都有 \(\sigma(b) \in B\)。\(B\) 是一个轨道,如果 \(B\) 是极小的稳定集合。\(P\) 是 transitive 的,当且仅当其没有非平凡稳定集合。
命题 所有轨道构成一个 \(A\) 的划分。
但实际上我们只需要的是
- 对内稳定
- 对外构成划分
这样我们就可以将问题分为两部分,其中第一部分可以递归处理。所以 orbit 是一个太严的概念。
定义 \(P \leq \text{Sym}(A)\) 是 transitive 的,\(B \subseteq A\),\(B\) 是其一个块 (block),当且仅当 \(B \neq A, B \neq \emptyset\),且 \(\forall \sigma \in P, \sigma(B) = B \text{ or } \sigma(B) \cap B = \emptyset\)。\(P\) 是 primitive 的,当且仅当其没有大小 \(>1\) 的 \(P\)-block。
命题 若 \(B\) 是一个块,则 \(\{\sigma(B) \mid \sigma \in P\}\) 构成了 \(A\) 的一个划分,称作块系统 (block system)。\(P\) 在 \(\{\sigma(B)\}\) 上有一个诱导作用 (induced action),也即一个定义在 \(\{\sigma(B)\}\) 上的 \(P'\),满足 \(P'(B) = P(B)\)。
于是可以递归解决 \(P'\) 上的问题。
定义 一个块系统是 minimal 的,如果其对应的诱导作用 \(P'\) 是 primitive 的。
由于一个 \(P\) 上的块系统和对应的 \(P'\) 在 \(\{\sigma(B) \mid \sigma \in P\}\) 上的块系统进行复合可以得到一个每个块更大的系统。所以 primitive 指出这里的 minimal 表示的是块数最少。而如果是 maximal 就表示块大小最小。
现在我们来简单研究块系统的结构。
命题 \(P\) 是一个 transitive 但不 primitive 的群,\(B\) 是其一个块,\(b \in B\),那么有 \(P_b \leq P_B \leq P\),且 \([P:P_B] = |\{\sigma(B) \mid \sigma \in P\}|, [P_B:P_b] = |B|\)。
这是轨道-稳定化子定理的简单应用。
命题 \(P \leq \text{Sym}(A)\) 且 transitive,\(b \in A\),那么如果 \(\exists K, \text{ s.t. } P_b < K < P\),那么 \(\exists B\) 是一个块,且 \(b \in B \subset A, |\{\sigma(B) \mid \sigma \in P\}| = [P:K], |B| = [K:P_b]\)。
证明 令 \(\{\sigma_1P_b, \ldots, \sigma_sP_b\}\) 是 \(P_b\) 在 \(K\) 中的陪集,\(s = [K:P_b]\),那么令 \(b_i = \sigma_i(b), B = \{b_1, \ldots, b_s\}\) 是一个满足条件的块。因为若 \(\sigma(B) \cap B \neq \emptyset\),考虑 \(b_i = \sigma(b_j)\),则 \(\sigma = \sigma_i \sigma_j^{-1}\),从而对任意 \(b_k\),都有 \(\sigma((\sigma_i^{-1} \sigma_j\sigma_k) \cdot b) = b_k\),找到 \(\sigma_i^{-1} \sigma_j \sigma_k\) 在哪个陪集里即可。从而 \(\sigma(B) = B\)。
同时我们可以知道,\(K \subseteq P_B, |K| = |P_B|\),故 \(K = P_B\)。这也就是说,块结构和包含了至少一个 \(P_b\) 的子群结构是对应的。这就像“保证所有操作的区间交不为空”那种 OI 题一样。
为了进一步加深这里的印象,我们再回顾一下轨道-稳定化子定理。
定理 (轨道-稳定化子, orbit-stabilizer) 令 \(G\) 是一个作用在有限集合 \(X\) 上的群,\(\text{Orb}(x)\) 表示 \(x\) 的轨道,\(G_x=\{\sigma(x) = x \mid \sigma \in G\}\),则有 \(|\text{Orb}(x)|=[G:G_x]\)。
证明 考虑定义 \(\phi_x:G \to \text{Orb}(x), \phi_x(g) = g \cdot x\),那么 \(\phi_x\) 是一个满射,且 \(\phi_x(g) = \phi_x(h)\) 当且仅当 \(g^{-1}h \in G_x\)。因此存在一个良定义的双射 \(G/G_x \to \text{Orb}(x), gG_x \to g \cdot x\)。由此可推得原命题。
也就是说,虽然 \(K\) 看起来只是单方面得到了 \(B\),从而 \(K \subseteq P_B\),但同时也立刻包含了所有的 \(P_B\)。因为如果有一些元素 \(g'\) 在 \(P_B\) 而不在 \(K\) 中,那么 \(g' \cdot x = g \cdot x\) 就会生成新的 \(g'g^{-1} \in P_b\),但是由于我们已经选取了全部的 \(P_b\),这是不可能的。所以 \(P_b < K\) 是重要的。
于是我们可以得到
引理 \(P \leq \text{Sym}(A), |A| > 1, |P| = p^l\),那么 minimal \(P\)-block system 有 \(p\) 个块。
证明 考虑诱导作用 \(P'\),作用在 \(A' = \{\sigma(B) \mid \sigma \in P\}\) 上。如果 \(|A| = p^t, t \geq 2\),那么任取 \(b \in A'\),有 \([P:P_b] = p^t\),根据 Sylow 定理,存在 \(P_b < K < P\),与 \(P'\) 是 primitive 的矛盾。
这不仅为我们提供了平缓的递归过程,也让 base case 变得 trivial。
接下来我们形式化这个想法。
定义 \(C_B(Q) = \{\forall b \in B, b \sim \sigma(b) \mid \sigma \in Q\}\),表示 \(Q\) 中保持 \(B\) 中颜色的集合。
首先,我们要看如何将两个子问题的结果合并。
命题 \(C_B(Q \cup Q') = C_B(Q) \cup C_B(Q'), C_{B \cup B'}(Q) = C_B(C_{B'}(Q))\)。
证明是显然的。
需要注意的是,我们并没有保证 \(Q\) 是一个群。因为在 block system 这里,每个块被表示为 \(\sigma \cdot B\),所以 \(Q\) 需要支持是一个陪集。
引理 若 \(C_B(\sigma P) \neq \emptyset\),则其是 \(C_B(P)\) 的一个陪集。也就是说,\(C_B\) 内的陪集可提出(代表元可能会变)。
证明 由于 \(B\) 在 \(P\) 是稳定的,\(C_B(P)\) 是一个群。任取 \(\alpha \in C_B(\sigma P)\) 我们想要证明 \(C_B(\sigma P) = \alpha C_B(P)\)。(a) \(\alpha C_B(P) \subseteq C_B(\sigma P)\): 任取 \(\beta \in C_B(P) \subseteq P\),\(\alpha \beta \in \sigma P\)。\(\forall v \in A, v \sim \beta(v) \sim (\alpha \beta)(v)\),因此 \(\alpha \beta \in C_B(\sigma P)\)。(b) \(C_B(\sigma P) \subseteq \alpha C_B(P)\): 任取 \(\gamma \in C_B(\sigma P), \alpha^{-1} \gamma \in C_B(P)\),这是由于 \(\alpha, \gamma \in C_B(\sigma P)\)。因此 \(\gamma = \alpha(\alpha^{-1} \gamma) \in \alpha C_B(P)\)。
接下来我们开始描述递归过程。
问题
- 输入:\(P \leq \text{Sym}(A)\),一个 \(2\)-group。\(B \subseteq A\),满足在 \(P\) 稳定,\(\sigma \in \text{Sym}(A)\)。
- 输出:\(C_B(\sigma P)\)。
- 初始条件:\(B = A, \sigma = id\)。
基于轨道的递归
如果 \(P\) 在 \(B\) 上不 transitive,\(B = B_1 \cup B_2\),其中 \(B_1, B_2\) 在 \(P\) 稳定,那么 \(C_B(\sigma P) = C_{B_1}(C_{B_2}(\sigma P))\)。
如何测试 \(P\) 在 \(B\) 是否 transitive?我们可以用一个 \(|B| \log |P|\) 的朴素算法。
基于块的递归
对于 \(2\)-group,其 minimal \(P\)-block system 一定形如 \(B = B_1 \cup B_2\)。那么 \(P\) 就形如 \(H \cup \tau H\),其中 \(H = P_{B_1} = P_{B_2}\),\(\tau\) 满足 \(\tau(B_1) = B_2, \tau(B_2) = B_1\)。
\[C_B(\sigma P) = C_B(\sigma H) \cup C_B(\sigma \tau H) = C_{B_1}(C_{B_2}(\sigma H)) \cup C_{B_1}(C_{B_2}(\sigma \tau H)) \]还有一个问题,就是结果的两侧都是 \(C_B(H)\) 的一个陪集,而我们已经知道它们的并是 \(C_B(P)\) 的一个陪集。
因为 \(\alpha, \beta \in C_B(\sigma P)\),所以 \(C_B(\sigma P) = \alpha C_B(P) = \beta C_B(P), \alpha^{-1} \beta \in C_B(P)\)。因此 \(\langle C_B(H), \alpha^{-1} \beta \rangle \subseteq C_B(P)\),所以有
\[\alpha\langle C_B(H), \alpha^{-1} \beta \rangle \subseteq C_B(\sigma P) = \alpha C_B(H) \cup \beta C_B(H) \]同时显然地,
\[\alpha C_B(H) \cup \beta C_B(H) \subseteq \alpha\langle C_B(H), \alpha^{-1} \beta \rangle \]故两者相同。
那么该如何找到 \(B_1, B_2\) 呢?
命题 (Sims) 在 \(P\) 下,最小的包含元素 \(a, b\) 的块是其在图 \(G = (B, E = \{\sigma(a), \sigma(b)\mid \sigma \in P\})\) 中的连通块。
证明不难。被放在了 Exercises 中。
那么重复执行这个操作,我们就可以得到一个 minimal block system,而上文已经保证了这样的块系统一定是只有两个块的。
Base case
\(|B| = 1\),其只包含一个 \(b\),\(P(B) = B\)。\(C_B(\sigma P) = \begin{cases}\sigma P & \sigma(b) \sim b \\ \emptyset & \text{otherwise}\end{cases}\)。
复杂度分析
设 \(f(s)\) 表示 \(|B| = s\) 时最多的递归调用次数。
基于轨道的递归,有
\[f(s) \leq f(s_1) + f(s - s_1) \]基于块的递归,有
\[f(s) \leq 4f\left(\frac s2\right) \]base case
\[f(1) = 0 \]经过简单推导,有 \(f(s) \leq s^2\)。
Lecture 4
我们如果回顾上述过程,会发现还有一点没有解决。就是在 \(P = H \cup \tau H\) 时,如何计算出这样的 \(H\)。更一般地,我们想解决这样的问题:
Input: 给定 \(P = \langle T \rangle \leq \text{Sym}(A), H\) 是 poly-index, poly-recognizable 的(i.e. \([P:H] = \text{poly}(|A|)\),给定 \(\sigma \in \text{Sym}(A)\) 可以在 \(\text{poly}(|A|)\) 测试是否有 \(\sigma \in H\))。
Output: \(H\) 的生成元集合。