主要可以解决一些生成函数问题,网上资料不是很多,orz zaky的博客。
part1 q-Binomial
考虑一个很经典的模型,就是从 \((0,0)\) 出发,每次向上或者向右走一格,走到 \((n,m)\) 的方案,这个方案数显然就是 \(\binom{n+m}{m}=\binom{n+m}{n}\)。
考虑比如 \(n=2,m=2\),可以得到下面一些行走路线,这些图被称为 Ferrers diagrams,直译过来就是费勒斯图。
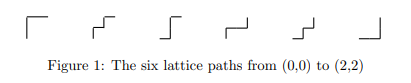
考虑这些行走路线右上角的部分有几个方格。
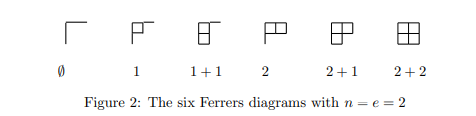
然后此时去定义这个 q-binomial,假设对于上面一种情况右上角方格数为 \(a_i\),那么定义 \(\begin{bmatrix}n+m\\m \end{bmatrix}_q=\sum q^{a_i}\),比如对于上面的例子,\(\begin{bmatrix}4\\2 \end{bmatrix}_q=1+q+2q^2+q^3+q^4\)。
此时考虑这个东西怎么去递推,令 \(q\) 为一个常数,\(f_{n,m}\) 为此时的值。
考虑上面格子的问题本质上是求一个长度为 \(m\) 的序列 \(b\),满足 \(b_i\le n,b_i\ge b_{i-1}\),然后答案就是 \(\sum_b q^{(\sum_{i=1}^m b_i)}\),那么直接 dp,那么 \(f_{i,j}\) 就表示前 \(i\) 个数,最后一个 \(\le j\) 的总和,那么容易得到转移方程:
\[f_{n,m}=f_{n,m-1}+f_{n-1,m}\times q^m \]那么可以得到
\[\begin{bmatrix}n+m\\m \end{bmatrix}_q=\begin{bmatrix}n+m-1\\m-1\end{bmatrix}_q+q^m\begin{bmatrix}n+m-1\\m \end{bmatrix}_q \tag{1}\\ \begin{bmatrix}n\\m \end{bmatrix}_q=\begin{bmatrix}n-1\\m-1\end{bmatrix}_q+q^m\begin{bmatrix}n-1\\m \end{bmatrix}_q \]然后还有个小推论:
\[\begin{bmatrix}n+m\\m \end{bmatrix}_q =\begin{bmatrix}n+m\\n\end{bmatrix}_q\tag{2} \]和组合数类似的式子,证明简单,考虑前面 \(n\times m\) 的矩形的意义即可,相当于旋转一下。
然后考虑 \(\begin{bmatrix}n\\m \end{bmatrix}_q\) 这个东西怎么求通项,当 \(q=0\) 时,显然 \(\begin{bmatrix}n\\m \end{bmatrix}_0=\dbinom{n}{m}\)。
结论是
\[\begin{bmatrix}n\\m \end{bmatrix}_q =\frac{\prod_{i=n-m+1}^n (1-q^i)}{\prod_{i=1}^m (1-q^i)}\tag{3} \]为了简记,定义 \([n]_q=\sum_{i=0}^{n-1}q^i,[n]!_q=\prod_{i=1}^n [n]_q\),那么可以发现
\[[n]_q=\sum_{i=0}^{n-1}q^i=\frac{1-q^n}{1-q}\\ [n]!_q=\frac{\prod_{i=1}^n (1-q^i)}{(1-q)^n}\\ \frac{[n]!_q}{[n-m]!_q\times [m]!_q}=\frac{\frac{\prod_{i=1}^n(1-q^i)}{(1-q)^n}}{\frac{\prod_{i=1}^{n-m}(1-q^i)}{(1-q)^{n-m}}\frac{\prod_{i=1}^m(1-q^i)}{(1-q)^m}}=\\ \frac{\prod_{i=1}^n(1-q^i)}{(\prod_{i=1}^{n-m}(1-q^i))(\prod_{i=1}^m(1-q^i))}=\frac{\prod_{i=n-m+1}^n (1-q^i)}{\prod_{i=1}^m (1-q^i)} \]那么就可以记为
\[\begin{bmatrix}n\\m \end{bmatrix}_q=\frac{[n]!_q}{[n-m]!_q\times [m]!_q}\tag4 \]这个东西和组合数非常像,因此很好记。
然后证明一下开始那个公式,用数学归纳法。
如果 \(m=1\),根据其意义可以简单得到方格个数显然 \([1,n]\) 中各一种,因此答案就是 \(\sum_{i=0}^n p^i=\frac{ (1-q^n)}{1-q}\),得证。
剩下的情况就是暴力展开,先咕着。
part 2 q-Binomial 定理
可以发现上面那个式子和组合数很像,那么就考虑一个类似的二项式定理。
回忆一下二项式定理:
\[(x+y)^n = \] 标签:begin,end,sum,笔记,学习,binomial,bmatrix,frac,prod From: https://www.cnblogs.com/houzhiyuan/p/16596667.html