第四周
知识回顾
-
巩固:2-SAT
-
深入研究:概率与期望
-
简单了解/没学明白:
练题
很麻烦的 2-SAT。
如果没有 x,就是个传统的问题。
然后我们发现 d 的取值很小,考虑对于每个 x 枚举其类型为 a 还是 c。
为什么不枚举 b 呢?因为 a、c 已经包含 b 了。
连边的时候编号要搞清楚,不然要调试很久。
复杂度 \(O(2^dn)\)。
神奇的期望题,花了好久才搞懂。
首先我们可以发现,只有所有的特殊数(在 \([l,r]\) 中没有因数)都被选了才能覆盖整个区间。
那么问题就转化为求出 \(t(p)\) 的期望值,也就是最后一个特殊数的位置,然后再将其乘以 \(n!\)。
定义 k 为特殊数的个数。现在考虑有多少非特殊数在最后一个特殊数的后面。
由于 k 个特殊点将序列分为 k+1 段,所以一个数在后面的概率为:
\[P=\frac{1}{k+1} \]然后根据 \(E(X+Y)=E(x)+E(y)\) 公式可知,n-k 个非关键点排在后面的个数的期望为:
\[E=(n-k)\cdot P=\frac{n-k}{k+1} \]怎么证明捏?
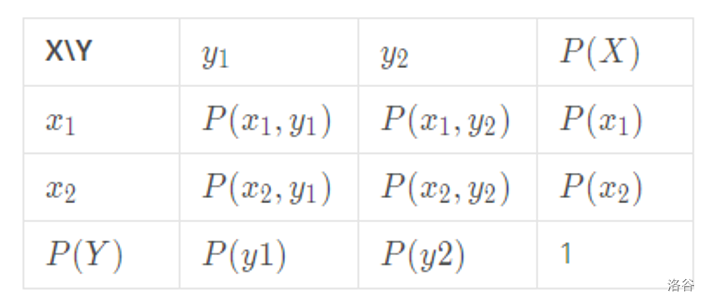
所以最后一个特殊数的期望位置为:
\[n-E=n-\frac{n-k}{k+1}=\frac{k\cdot(n+1)}{k+1} \]最后乘上 \(n!\) 就行了,最终答案为:
\[\frac{k}{k+1}\cdot (n+1)! \]k 可以筛出来。
模拟赛
省选计划
三道 lxl 毒瘤青蛙题。
20+25+20=65 rk30。
T304433 A. 虚空处刑【省选计划 · 模拟赛 #3】
对序列按 \(\sqrt n\) 大小分块。
这个信息是分治信息。
对每个块分类讨论:
-
这个块只有一种颜色。
-
这个块内有多种颜色。
对于 2 情况,维护这个块内的每个颜色的分治信息。每次进行范围 \([l,r]\) 染色为 c 的操作时,会把一些完整的块变成颜色为 c 的,以及把 \(O(1)\) 个块内部进行一次区间染色为 c 的操作。
同色块的颜色从 b 变为 c 只需要 \(O(1)\) 的时间处理,块内部区间染色可以使用颜色段均摊,等价于进行了 \(O(n+m)\) 次颜色段的修改,每次修改可以 \(O(\sqrt n)\) 代价重构零散块。
每次查询 \([l,r]\) 时,在左右两端的块内查询出该颜色的分治信息,然后在中间的块中,若一个块只有一种颜色,则可以 \(O(1)\) 计算出其分治信息,否则直接取该颜色对应的块内分治信息。
之后按顺序合并分治信息即可。
总时间复杂度 \(O((n+m)\sqrt n)\)。
T304327 B. 超人机械【省选计划 · 模拟赛 #3】
由于只有叶子的 v 初始非零,且叶子的 v 不变,容易证明所有点的 v 是单调不减的,于是每个点每一时
刻的 v 是上一时刻的 v 对孩子上一时刻的 v 取 max。
对树进行轻重链剖分,转化为维护序列,初值全零,支持单点增大(轻子树对重链的影响),每一时刻序列每个位置 x 变为上一时刻位置 x, x+1 的最大值(重链上的情况),查询区间最小值、最大值、和。可以用平衡树维护相邻相同的值构成的段,均摊地删去长度变为 0 的段。
时间复杂度 \(O((n+m)\log^2 n)\)。
T304328 C. 堕天作战【省选计划 · 模拟赛 #3】
将点集分为未移动的部分和移动过的部分维护,移动过的点按最后一次移动的 o 分类维护。
对于最后一次移动的 o=1(o=2)的点维护 x(y)的前缀的点数。
定义分界线为已进行的修改操作的 (x,y) 的左下方区域的并的边界。
移动过的点都在分界线上,未移动的点都在分界线上或右上方。
分界线可以用若干段水平或竖直的线段表示,每次修改操作造成均摊 \(O(1)\) 次线段插入删除,需要找出
这次操作中首次发生移动的点,并维护发生变化的线段上的点。
以 o=1 为例,需要删除若干竖直线段,合并多条水平线段,找出这次操作中首次发生移动的点。
查询 (X,Y) 左下方的点数,如果 (X,Y) 在分界线的左下方,则答案0,否则可以差分为查询 (X,Y) 上方、右方、右上方的点数,右上方的点都没有移动过,可以在初始给的点集上查询矩形和,上方和右方可以在动态维护的未移动/移动过的点集中查询前缀和。
时间复杂度 \(O((n+m)\log n)\)。
标签:移动,颜色,省选,查询,cdot,计划,frac,四周 From: https://www.cnblogs.com/HQJ2007/p/17561596.html