- 三元组损失 triplet loss

设计初衷:
让x与这个跟他同类的点距离更近,跟非同类的点距离更远。
d是距离,m的含义是,当x与x+的距离减去x与x-,如果小于-m时,对损失函数的贡献为0,
如果大于-m时,对损失的贡献大于0.
含义就是:当负例太简单时,不产生损失,这个损失的目标是,挑选困难样本进行分类。
这个损失函数的缺陷:
一个正例只能和一个负例进行对比。效率较低。
这个损失函数,算法如何求解?
2. InfoNCE损失


注意一点:
一个样本点u,一个正样本点和多个负样本点。而不是一个u,分子是u和多个正样本点的内积做exp。
如果对infonce改写,分子内积求和依然可以。但是从infonce的推导上不可以。
为什么?
3. hinge loss
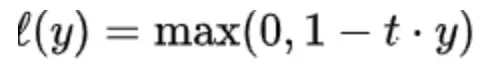
t>0,是一个超参数。
当y<1/t时,l(y)大于0。说明该样本点贡献了损失。
当y>1/t时,l(y)等于0。说明该样本点没有贡献损失。
4. pairwise ranking loss
当两者不是同一个类的时候,如果两个的距离小于m,则贡献了损失,如果大于m则没有贡献损失。
可以从困难样本、简单样本角度来理解,只有困难样本才会拿去训练,简单样本不会拿去训练。
也可以从这个角度理解:当两个不属于同一类别,但是距离又比较近的时候,应该对其进行惩罚,让两者的距离变远。
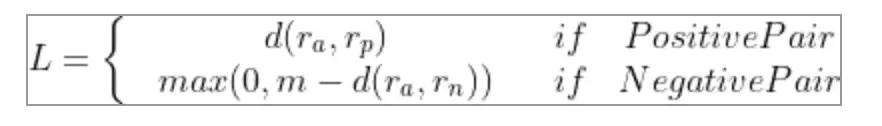
上面两个式子,可以统一为下式,当y为1时,时positive pair。仅保留了前面那个距离。
当y为0时,仅保留了后面那个式子。
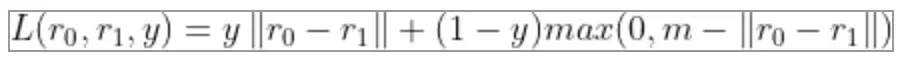
这个损失函数缺点是:每次仅考虑两个样本。
且m是超参数。
5. BPR算法,贝叶斯个性化排序(Bayesian Personalized Ranking, 以下简称BPR)
是用来做矩阵分解的,一般来说是评分矩阵,分解为W矩阵和H矩阵的乘法,求解W矩阵和H矩阵。
推荐系统遇上深度学习(二十)--贝叶斯个性化排序(BPR)算法原理及实战
标签:NLP,函数,loss,样本,矩阵,损失,四十七,距离 From: https://www.cnblogs.com/zhangxianrong/p/17558297.html