什么是数学规划

通俗地讲就是求目标函数在一定的约束条件下的极值问题
一般形式：
min 或者max z = f(x) x:决策变量（一般有多个自变量）

数学规划问题的分类

1、线性规划问题
如果目标函数和约束条件均是线性表达式，那么此时的数学规划问题就属于线性规划问题
2、非线性规划问题
3、整数规划问题
4、0-1规划问题（整数规划问题的分类）

线性规划问题

matlab中线性规划的标准型

如果让我们求f(x)的最大值，我们只需要求-f(x)的最小值

A是我们不等式约束的系数矩阵， b是不等式约束的常数项， lb是下界、ub是上界（不写默认是正无穷）


例题

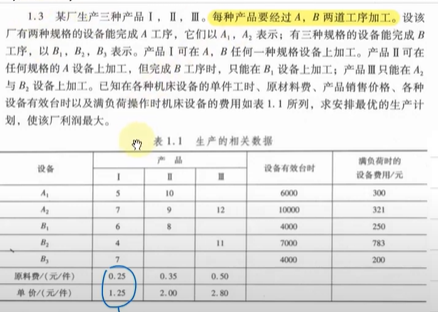
线性规划问题的难点在于列出目标函数、不等式条件、等式条件

整数规划问题

0-1规划

c = [-20, -10]';
intcon = [1, 2];
A = [5 4; 2 5];
b = [24; 13];
lb = zeros(2, 1);
[x, fval] = intlinprog(c, intcon, A, b, [], [], lb);
fval = -fval

背包问题

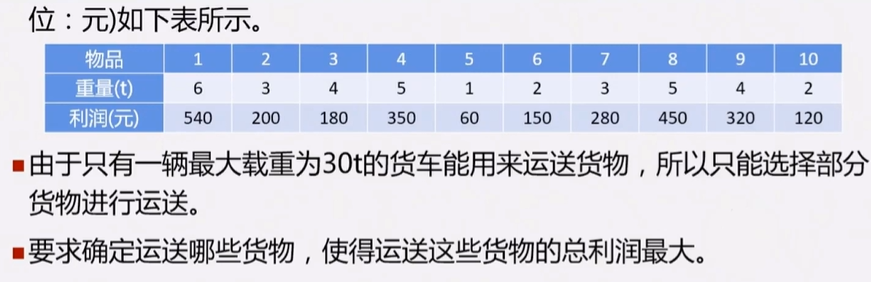
分析：

%% 背包问题
c = -[540 200 180 350 60 150 280 450 320 120];
%% 整数变量的位置，一共10个决策变量，均为整数
intcon = [1:10];
A = [6 3 4 5 1 2 3 5 4 2];
b = 30;
lb = zeros(1, 10);
ub = ones(1, 10);
[x, fval] = intlinprog(c, intcon, A, b, [], [], lb, ub);
fval = -fval
x

非线性规划问题

约束条件既可以出现线性约束条件也可以出现非线性约束条件

例子

求非线性规划的函数


关于非线性规划问题的初始值如何确定网课中比较推荐的是用蒙特卡罗算法去找（什么是蒙特卡罗还不太清楚，等看了再把这补上）。