搞一点计数题放在这,看到有意思的计数就更(虽然在组合数学那已经更了好多了)。
[CTSC2017] 吉夫特
给定一个长度为 \(n\) 的序列 \(a\),保证 \(a_i\) 互不相同。求出有多少个长度大于等于二的序列满足
\[\prod _{i=2}^{k} \binom{a_{b_{i-1}}}{a_{b_i}} \bmod 2 = \binom{a_{b_1}}{a_{b_2}} \times \binom{a_{b_2}}{a_{b_3}} \times \cdots \binom{a_{b_{k-1}}}{a_{b_k}} \bmod 2 > 0 \]方案数对 \(10^9+7\) 取模。
数据范围:\(n\le 211985, a_i\le 233333\)。
我们考虑这个序列的性质,即这些组合数中不能出现偶数。我们考虑如何利用这个性质。
我们把组合数的计算公式搬出来:\(\dbinom{n}{m}=\frac{n!}{m!(n-m)!}\),为了让它为奇数,我们需要让上下阶乘的 \(2\) 的个数相等。
我们考虑把阶乘分解,设 \(f(x)\) 为 \(x!\) 所含的 \(2\) 的个数,则易得:
\[f(x)=\sum_{i=1}^{+\infty} \frac{x}{2^i} \]我们再设 \(g(x)=x\),\(h(x)\) 为 \(x\) 二进制中 \(1\) 的个数,则
\[\begin{aligned} g(x)&=g(\frac{x}{2})+\frac{x}{2}+(x\bmod 2)\\ &=\sum _{i=1}^{+\infty} \frac{x}{2^i}+h(x) \\ &=f(x)+h(x) \end{aligned} \]则 \(f(x)=g(x)-h(x)=x-h(x)\)。再根据需要让上下阶乘 \(2\) 的个数相等,能得出来 \(h(n)=h(m)+h(n-m)\),即 \(n\) 二进制下 \(1\) 的个数等于 \(m\) 二进制下 \(1\) 的个数加 \(n-m\) 二进制下 \(1\) 的个数。我们考虑如何满足这个条件。
考虑 \(n=(\cdots 00100\cdots)_2, m=(\cdots 00010\cdots)_2\),那么 \(n-m=(\cdots 00010\cdots)_2\)。显然不可能 \(1\) 的个数相等,因此我们必须满足 \(m\) 是 \(n\) 的子集。
这样就好做了。我们先把所有数存一下位置,从后往前扫,枚举 \(a_i\) 的子集,看是否在 \(i\) 后面,转移即可。
时间复杂度:\(O(\mathrm{能过} )\)。
[HNOI2012] 集合选数
给定一个集合 \(\{1, 2, 3\cdots n \}\),问有多少满足下述限制的子集:如果 \(x\) 在该集合中,那么 \(2x, 3x\) 不能在该集合中。
数据范围:\(n\le 10^5\)。
很有意思的一道题。
我们考虑从一个数为左上角开始构造出一个矩阵,这个矩阵每个数都是它左边数的 \(2\) 倍,是它上面的数的 \(3\) 倍。比如以 \(1\) 为例,构建出的矩阵即为:
\[\begin{bmatrix} 1& 2& 4& 8& \cdots&\\ 3& 6& 12& 24& \cdots&\\ 9& 18& 36& \cdots &\cdots&\\ 27& \cdots& \cdots& \cdots& \cdots&\\ \cdots &\cdots &\cdots &\cdots &\cdots \end{bmatrix} \]这样,我们就把问题转化为了:在这个矩阵中选择数字,满足选择的数字不相邻。同时我们发现,每个矩阵的方案互不干扰。我们就可以每个矩阵求一遍。
不难看出,这个矩阵的大小最多为 \(\log_2 n\times \log_3 n\)。我们可以直接状压 dp,是一个比较经典的状压 dp 问题。可以直接用插头 dp 解决。
时间复杂度:\(O(\mathrm{能过})\)。
城市规划
求 \(n\) 个点有标号连通图的个数。
数据范围:\(n\le 130000\)。
本题可能不是那么精妙,但是是下一道题的前置。
我们设 \(c_i\) 为 \(i\) 个点有标号连通图个数,\(\varphi(i)\) 为 \(i\) 个点的图的个数,易知 \(\varphi(x)=2^{\frac{x(x-1)}{2} }\),只需要看点与点之间的边是否在图中即可。
我们考虑容斥,求出不连通图的个数。我们可以枚举一号点所在连通块的大小,就能得到转移方程
\[c(n)=\varphi(n)-\sum \limits _{i=1}^{n-1}\dbinom{n-1}{i-1}c_i\varphi(n-i) \]这个转移方程右半部分的含义是:\(1\) 号点所在连通块的方案数为 \(c_i\),同时我们需要选出 \(i-1\) 个点和它在一个连通块中。剩下的点就不用管了,形成任意的图都可以。
考虑加速计算这个式子:
\[\begin{aligned} c_n&=\varphi(n)-\sum \limits _{i = 1}^{n-1}\frac{(n-1)!}{(i-1)!(n-i)!}c_i\varphi(n-i)\\ \frac{c_n}{(n-1)!} &=\frac{\varphi(n)}{(n-1)!}- \sum \limits _{i = 1}^{n-1}\frac{c_i}{(i-1)!}\frac{\varphi(n-i)}{(n-i)!} \end{aligned} \]设 \(\phi (x)=\frac{c(x)}{(x-1)!}\),\(\pi (x)=\frac{g(x)}{x!}\)。那么上面的式子就变为了
\[\phi(n)=\frac{g(n)}{n!}-\sum \limits_{i=1}^{n-1}\phi (i)\pi(n-i) \]直接分治 FFT 即可。时间复杂度 \(O(n\log^2 n)\)。
How Many of Them
求有 \(n\) 个点,割边数量不超过 \(m\) 的无向连通图的数量。
数据范围:\(n, m\le 50\)。
比较 nb 的不用多项式的图论计数。
我们设 \(F[i, j]\) 为 \(i\) 个点,\(j\) 条割边的无向连通图的数量。我们考虑去掉 \(1\) 号点所在的双连通分量,那么整张图就会分为一堆连通块。我们再设 \(G[i, j, k]\) 为 \(i\) 个点,\(j\) 条割边,\(k\) 个连通块的无向图的数量。那么我们枚举 \(1\) 号点所在连通分量的大小,就能对于 \(0<j<i\) 得到转移方程:
\[F[i, j]=\sum \limits _{p=1}^{i-1}(F[p, 0]\times\dbinom{i-1}{p-1}\times \sum \limits _{q=1}^j (G[i-p,j-q,q]\times p^q)) \]\(p\) 枚举的是 \(1\) 号点所在连通分量的大小,\(q\) 枚举的是 \(1\) 号点所在的连通分量去掉后会剩下多少连通块,而割边也会随之减少 \(q\),可以看下图理解:
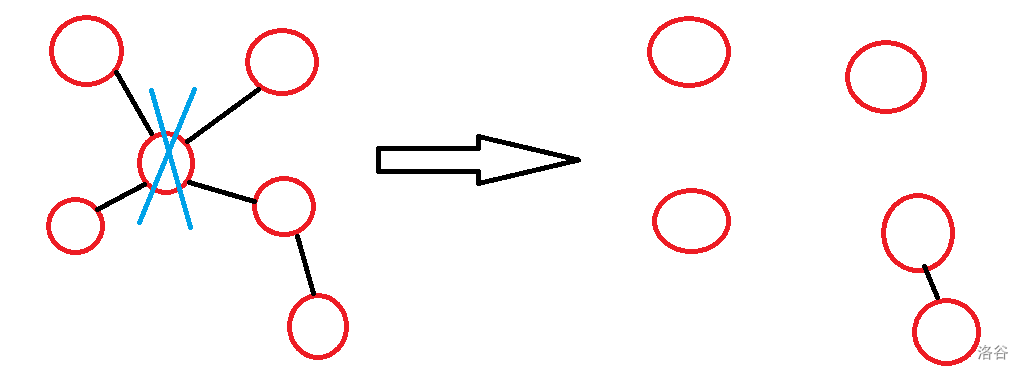
然后 \(p^q\) 的含义即为我们每个连通分量一定会选择 \(1\) 号点所在的连通块中一个点连边,那么方案数即为 \(p^q\)。
再考虑求出 \(F[i, 0]\)。根据容斥,我们只需要用连通图的数量减去含割边的图的数量即可,而连通图的数量则看上一道题。因此:
\[F[i, 0]=c_i-\sum \limits _{j=1}^{i-1}F[i,j] \]最后我们再考虑求出 \(G\) 数组。我们依旧枚举 \(1\) 号点所在连通块大小 \(p\),同时我们再枚举一号点连通块割边的数量 \(q\),我们就能得到转移方程:
\[G[i,j,k]=\sum\limits_{p=1}^i\sum\limits _{q=0}^j(f[p,q]\times p\times \dbinom{i-1}{p-1}\times G[i-p,j-q,k-1]) \]我们注意到其中多乘了一个 \(p\),这其实代表着我们求出的是“有根双连通分量”,因为我们要在这个双连通分量中选一个点来和一开始去掉的边双连边。因此我们多乘了一个 \(p\),而在别的情景中需要视情况而定。
时间复杂度:\(O(n^5)\)。