复数与三角函数是学习OI数学中比较基础的内容,对于初中选手不是很友好。
定义
三角函数
三角函数最初是用来表示直角三角形三边关系的函数。
复数
定义一个常数 \(i=\sqrt{1}\),那么所有形如 \(a+bi\) 的数都是复数。(\(a,b\in \R\))
一般用 \(z\) 表示复数。
下文中的 \(\pi=180\degree\)。
一般我们考虑复数的几何意义,都在复平面上考虑。
复平面长成下面这个样子:
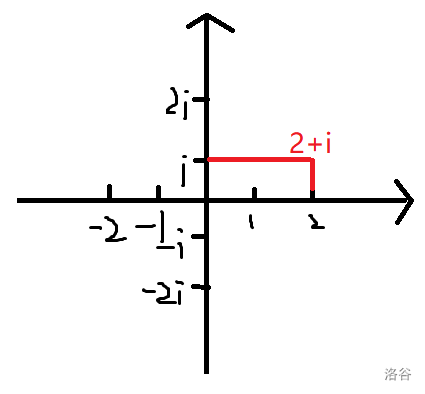
在这个坐标系上点 \((a,b)\) 所代表的值为 \(a+bi\)。
不难发现在这个坐标系上一个点只能代表一个复数,一个复数恰好对应一个点。
向量是同时具有方向和大小的量,在几何中用带箭头的线段表示,这个线段的长度及其箭头所指方向与其表示的内容相关。
以实轴正方向为始边,\(z\) 所对应的向量 \(Z\) 为终边的角 \(\theta\) 称为复数 \(z\) 的幅角。
大概就像下图这个样子:
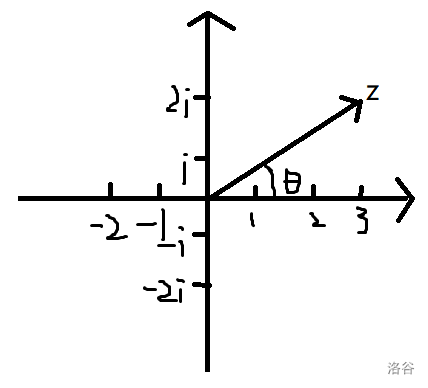
运算
复数的模
复数 \(z=a+bi\) 的模为其复平面上对应的向量的长度记作 \(|z|\)。\(|z|\) 的计算公式为
\[|z|=\sqrt{a^2+b^2} \]可以理解为这个数就是复数 \(z\) 到复平面上原点的距离。
共轭复数
复数 \(z\) 的共轭复数是由 \(z\) 沿着复平面实数轴(\(x\) 轴)反转得到的,记为 \(\overline{z}\)。
\(z\) 与 \(\overline{z}\) 之间有以下的性质:
- 设 \(z\) 的幅角为 \(\theta_0\),\(\overline{z}\) 的幅角为 \(\theta_1\),则 \(\theta_0+\theta_1=2\pi\)。
- \(|z|=|\overline{z}|\)
- 若 \(z=a+bi\),则 \(\overline{z}=a-bi\)。
复数运算
假设有两个复数 \(z_1=a_1+b_1i\) 和 \(z_2=a_2+b_2i\)。
\[z_1\pm z_2=(a_1\pm b_1i)+(a_2\pm b_2i)=(a_1\pm a_2)+(b_1\pm b_2)i\\ \\ z_1\times z_2=(a_1+b_1i)\times(a_2+b_2i)=a_1a_2+a_1b_2i+a_2b_1i+b_1b_2i^2\\ \because i^2=-1\\ \therefore z_1\times z_2=(a_1a_2-b_1b_2)+(a_1b_2+a_2b_1)i\\ \\ \frac{z_1}{z_2}=\frac{z_1\overline{z_2}}{z_2\overline{z_2}}=\frac{z_1\overline{z_2}}{(a_2+b_2i)(a_2-b_2i)}=\frac{z_1\overline{z_2}}{a_2^2+b_2^2} \]