2021-2022年丘成桐女子中学生数学竞赛——笔试部分
声明:本文为我从网上流传的试题写的个人解答,与清华大学求真书院官方无关。首届丘成桐女子中学生数学竞赛于2021年10月31日晚落下帷幕,共140名左右学生参加了笔试,35名学生入围面试,争夺“诺特奖”,最终决出金奖、银奖、铜奖、优胜奖各1、3、6、15人。
下面来看看这份题是长什么样子,除了第3题我没什么把握做对、第6题(图论)完全不会,其他应该都没做错吧,如果有误敬请指出。
2021-2022年丘成桐女子中学生数学竞赛——笔试部分
第1题 已知\int_{-\infty}^{+\infty}e^{-x^2}\mathrm{d}x=\sqrt{\pi}, 给定正实数X,x_0,\delta, 试求
\lim_{n\to+\infty}\sqrt{n}\int_{x_0-\delta}^{x_0+\delta}e^{-nX(x-x_0)^2}\mathrm{d}x \\ 的值.
解: 注意到(第三行换元y=\sqrt{nX}x.)
\begin{aligned} I_1(n)&:= \sqrt{n}\int_{-\infty}^{+\infty}e^{-nX(x-x_0)^2}\mathrm{d}x\\ &=\sqrt{n}\int_{-\infty}^{+\infty}e^{-nXx^2}\mathrm{d}x \\ &=\sqrt{n}\dfrac{1}{\sqrt{nX}}\int_{-\infty}^{+\infty}e^{-y^2}\mathrm{d}y \\ &=\dfrac{\sqrt{\pi}}{\sqrt{X}}. \end{aligned}\\
并且
\begin{aligned} I_2(n)&:= \sqrt{n}\int_{(-\infty,x_0-\delta)\cup(x_0+\delta,+\infty)}e^{-nX(x-x_0)^2}\mathrm{d}x \\ &< 2\sqrt{n}\int_{x_0+\delta}^{\infty}e^{-nX\delta(x-x_0)}\mathrm{d}x \\ &=2\sqrt{n}\cdot \dfrac{1}{nX\delta}e^{-nX\delta^2}\to 0(n\to\infty) \end{aligned}
因此
\begin{aligned} &\quad \lim_{n\to+\infty}\sqrt{n}\int_{x_0-\delta}^{x_0+\delta}e^{-nX(x-x_0)^2}\mathrm{d}x \\ &=\lim_{n\to+\infty}(I_1(n)-I_2(n))=\boxed{\dfrac{\sqrt{\pi}}{\sqrt{X}}}. \end{aligned}\\
第2题 (1)求\sin x在x=0处的泰勒级数.
(2)判断极限\lim\limits_{n\to+\infty}(n!\sin 1-\lfloor n!\sin 1\rfloor)是否存在, 若存在, 求出该极限的值. 若不存在, 请说明理由. 其中\lfloor t\rfloor表示不超过t的最大整数.
解: (1)设f(x)=\sin x, 则f^{(n)}(x)=\sin\left(x+\dfrac{n\pi}{2}\right), 当n=2k-1为奇数时, f^{(2k-1)}(0)=(-1)^{k-1}; 当n=2k为偶数时, f^{(2k)}(0)=0. 由泰勒展开的公式可得
\boxed{\sin x=\sum\limits_{k=1}^{\infty}\dfrac{(-1)^{k-1}}{(2k-1)!}x^{2k-1}}. \\
(2)该极限不存在. 证明如下: 考虑奇子列\{(2n-1)!\sin 1-\lfloor(2n-1)!\sin 1\rfloor\}.
注意到当n=2m-1时, 有 \sin x\le \sum\limits_{k=1}^{n}\dfrac{(-1)^{k-1}}{(2k-1)!}x^{2m-1}, \qquad \forall x>0,
当n=2m时, 有 \sin x\ge \sum\limits_{k=1}^{n}\dfrac{(-1)^{k-1}}{(2k-1)!}x^{2m-1}, \qquad \forall x>0,
接下来, 由于
\begin{aligned} &\quad (2n-1)!\sin 1=\sum\limits_{k=1}^{\infty}\dfrac{(-1)^{k-1}(2n-1)!}{(2k-1)!} \\ &=\sum\limits_{k=1}^{n}\dfrac{(-1)^{k-1}(2n-1)!}{(2k-1)!}+ \sum\limits_{k=n+1}^{\infty}\dfrac{(-1)^{k-1}(2n-1)!}{(2k-1)!} \\ &:=S_1+S_2, \end{aligned}\\
注意S_1是整数, 当n>1时,
\begin{aligned} \left|S_2\right| &\le\sum\limits_{k=n+1}^{\infty}\dfrac{(2n-1)!}{(2n-1)!(2k-1)(2k-2)} \\ &\le \sum\limits_{k=n+1}^{\infty}\dfrac{1}{(2k-1)(2k-3)} =\dfrac{1}{2(2n+1)} < \dfrac{1}{2} \end{aligned}\\
于是当n=2m-1时, S_2= (2n-1)!\sin 1-S_1 < 0, 即-\dfrac{1}{2} < S_2 < 0, 此时
\lfloor(2n-1)!\sin 1\rfloor = 1+\sum\limits_{k=1}^{m}\dfrac{(-1)^{k-1}(2n-1)!}{(2k-1)!}.\\
当n=2m时, S_2=(2n-1)!\sin 1-S_1>0, 即0 < S_2 < \dfrac{1}{2}. 此时
\lfloor(2n-1)!\sin 1\rfloor = \sum\limits_{k=1}^{m}\dfrac{(-1)^{k-1}(2n-1)!}{(2k-1)!}.\\
另一方面, 由前面的推导可得|S_2|\to 0(n\to\infty), 因此数列\{(2n-1)!\sin 1-\lfloor(2n-1)!\sin 1\rfloor\}的奇子列收敛于1, 偶子列收敛于0, 所以数列\{(2n-1)!\sin 1-\lfloor(2n-1)!\sin 1\rfloor\}是发散的. 所以原数列存在发散子列, 则原数列也是发散. \square
第3题 设\mathbb{C}为全体复数构成的集合, n是正整数. 定义映射
\begin{aligned} f:&\mathbb{C}^n\times\mathbb{C}^n\times\mathbb{C}^n\to \mathbb{C}^n\times\mathbb{C}^n\times\mathbb{C}^n, \\ &(X,Y,Z)\mapsto (X+Y+Z,X+\omega Y+\omega^2Z,X+\omega^2Y+\omega Z), \end{aligned}\\ 其中\omega=-\dfrac{1}{2}+\dfrac{\sqrt{3}}{2}i, i=\sqrt{-1}是虚数单位.
(1)证明f是线性同构.
(2)A,B,C都是复数域上的n阶方阵. 定义矩阵
M=\begin{pmatrix} A&B&C\\C&A&B\\B&C&A\end{pmatrix}. \\ 证明: M的全体特征值构成的集合是A+B+C,A+\omega B+\omega^2C,A+\omega^2B+\omega C特征值构成的集合的并.
证明(不保证正确): (1)f线性是显然的, 下证f是单射. 若
\left\{\begin{aligned} &X+Y+Z=0, \\ &X+\omega Y+\omega^2Z=0, \\ &X+\omega^2Y+\omega Z=0, \end{aligned}\right.\\
这是一个关于文字X,Y,Z的线性方程组, 其系数矩阵的行列式为
\left|\begin{matrix} 1&1&1 \\ 1&\omega&\omega^2 \\ 1&\omega^2&\omega \end{matrix}\right|=\left|\begin{matrix} 1&1&1 \\ 1&\omega&\omega^2 \\ 1&\omega^2&\omega^4 \end{matrix}\right|=(1-\omega)(1-\omega^2)(\omega^2-\omega^4)\ne 0,\\
(Vandermonde行列式性质), 所以该线性方程组只有零解(X,Y,Z)=(0,0,0), 从而f是单射.
由于线性空间中一个线性映射是单射当且仅当它是满射, 所以f是同构.
(2)记矩阵X=\begin{pmatrix} &I&\\&&I\\I&&\end{pmatrix}. 其中I是n阶单位矩阵. 容易求得X的特征多项式是(\lambda^3-1)^n, 所以X的所有特征值为1,\omega,\omega^2(都是n重). 记e_i=(\cdots,0,1,0,\cdots)^T\mathbb{C}^n(第i个分量是1, 其余分量是0)(i=1,2,\cdots,n), 那么对应于1的所有线性无关特征向量为\begin{pmatrix}e_i \\ e_i \\ e_i\end{pmatrix}, 对应于\omega的所有线性无关特征向量为\begin{pmatrix}\omega e_i \\ \omega^2 e_i \\ e_i\end{pmatrix}, 对应于\omega^2的所有线性无关特征向量为\begin{pmatrix}\omega^2 e_i \\ \omega e_i \\ e_i\end{pmatrix},
M可以表示为
M=f(X)=\begin{pmatrix}A\\&A\\&&A\end{pmatrix} +\begin{pmatrix}B\\&B\\&&B\end{pmatrix}X +\begin{pmatrix}C\\&C\\&&C\end{pmatrix}X^2.\\
设X的一个特征值为\lambda, 对应特征向量为v, 则
\begin{aligned} Mv&=f(X)v=\begin{pmatrix}A\\&A\\&&A\end{pmatrix}v +\begin{pmatrix}B\\&B\\&&B\end{pmatrix}Xv +\begin{pmatrix}C\\&C\\&&C\end{pmatrix}X^2v \\ &=\begin{pmatrix}A\\&A\\&&A\end{pmatrix}v +\begin{pmatrix}B\\&B\\&&B\end{pmatrix}\lambda v +\begin{pmatrix}C\\&C\\&&C\end{pmatrix}\lambda^2v \\ &=\begin{pmatrix}A+\lambda B+\lambda^2C\\&A+\lambda B+\lambda^2C\\&&A+\lambda B+\lambda^2C\end{pmatrix}v \\ &:=\mathrm{diag}_3(A+\lambda B+\lambda^2C)v. \end{aligned}\\
由于X共有3n个线性无关特征向量, 故任意向量v\in\mathbb{C}^{3n}均可以写成X的所有特征向量的线性组合. 因此\mathrm{diag}_3(A+\lambda B+\lambda^2C)的特征值也是M的特征值. 从而A+\lambda B+\lambda^2C(\lambda=1,\omega,\omega^2)的特征值都是M的特征值. \square
第4题 设S是全体单位复数的乘法群, 判断S的有限子群是否一定为循环群, 并说明理由.
证明: 是. 我们只需证明如下断言: 若G是n元有限Abel群, 且对任意d|n, 方程x^d=1的根的个数不超过d, 则G是循环群.
证明如下: 假设G_d由G的所有d阶元构成, 且G_d\ne\varnothing, 于是有y\in G_d.
显然由y生成的群\langle y\rangle\subseteq\{x\in G|x^d=1\}, 但是\langle y\rangle=\{1,y,\cdots,y^{d-1}\}, 由于方程x^d=1根的个数不超过d, 故\langle y\rangle\supseteq\{x\in G|x^d=1\}, 所以\langle y\rangle=\{x\in G|x^d=1\}. 因此|G_d|=\phi(d).
于是我们证明了G_d要么是空集, 要么|G_d|=\phi(d). 对任意d|n, 有
n=|G|=\sum_{d|n}|G_d|\le\sum_{d|n}\phi(d)=n, \\
所以对任意d|n都有|G_d|=\phi(d), 故G是循环群. \square
在本题中, 由于S的有限子群G是有限Abel群, 且对任意d, 方程x^d=1都不超过d个, 由前面的断言, G是循环群. \square
注: Euler示性函数\phi(d)表示不超过d且与d互素的正整数个数. 比如\phi(6)=1, \phi(8)=3.
参考:
第5题 对任意矩阵A, 定义\|A\|=\sqrt{\mathrm{tr}(A^TA)}. 如果A满足A^TA=AA^T=I, 其中I是单位矩阵, 称A为正交矩阵.
(1)求证: 若P,Q为实正交矩阵, 则对实矩阵A, 有\|A\|=\|PAQ\|.
(2)A为n阶实对称矩阵, v是任意n维实列向量. 设\lambda_1,\cdots,\lambda_n是A的全体特征值, 证明:
\|Av\|\le\max\{|\lambda_1|,\cdots,|\lambda_n|\}\|v\|. \\ (3)A为n阶实对称矩阵, v是任意n维实列向量. 证明:
\|A\|^2\ge\dfrac{2n-1}{2(n-1)}\dfrac{\|Av\|^2}{\|v\|^2}-\dfrac{1}{n-1}[\mathrm{tr}(A)]^2. \\
证明: (1)利用熟知的等式\mathrm{tr}(ABC)=\mathrm{tr}(BCA)(A,B,C\text{为方阵}), 可得
\begin{aligned} \|PAQ\|&=\sqrt{\mathrm{tr}[(PAQ)^T(PAQ)]} \\ &=\sqrt{\mathrm{tr}(Q^TA^TP^TPAQ)} \\ &=\sqrt{\mathrm{tr}(Q^TA^TAQ)} \\ &=\sqrt{\mathrm{tr}(A^TAQQ^T)} \\ &=\sqrt{\mathrm{tr}(A^TA)}=\|A\|. \end{aligned}\\
(2)由于A是实对称矩阵, 故可以对角化, 记A=P\Lambda Q, 其中\Lambda=\mathrm{diag}(\lambda_1,\cdots,\lambda_n), 令w=Qv=(w_1,w_2,\cdots,w_n)^T, 则
\|w\|=\sqrt{\mathrm{tr}(v^TQ^TQv)}=\sqrt{\mathrm{tr}(v^Tv)}=\|v\|, \\
且
\begin{aligned} \|Av\|^2&=\|P\Lambda Qv\|^2=\mathrm{tr}(v^TQ^T\Lambda^TP^TP\Lambda Qv)\\ &=\mathrm{tr}(w^T\Lambda^T\Lambda w) =\sum\limits_{i=1}^n\lambda_i^2w_i^2 \\ &\le \max\{|\lambda_1|,\cdots,|\lambda_n|\}^2\sum\limits_{i=1}^nw_i^2 \\ &=\max\{|\lambda_1|,\cdots,|\lambda_n|\}^2\|w\|^2 \\ &=\max\{|\lambda_1|,\cdots,|\lambda_n|\}^2\|v\|^2. \end{aligned}\\
(3)由(1), \|A\|^2=\|\Lambda\|^2=\lambda_1^2+\cdots+\lambda_n^2, 注意到\mathrm{tr}(A)=\lambda_1+\cdots+\lambda_n(特征值与特征多项式的关系), 故
(\mathrm{tr}(A))^2=(\lambda_1^2+\cdots+\lambda_n^2)+\sum\limits_{i\ne j}\lambda_i\lambda j. \\
之前的答案有误,待修改
第6题 已知图T为树, 其顶点V_1,\cdots,V_n的度依次为d_1,\cdots,d_n, 其中d_i\in\mathbb{N}^*, i=1,2,\cdots, \sum_{k=1}^nd_k=2n-2.来源:Fiddie的数学之旅,https://zhuanlan.zhihu.com/p/427999097 清华大学 数学竞赛 丘成桐数学竞赛 丘成桐(数学家)
(1)证明: 满足条件的不同树的个数为 \dfrac{(n-2)!}{(d_1-1)!(d_2-1)!\cdots(d_n-1)!}.
(2)记所有含有n个顶点的树构成的集合为S, 证明恒等式:
(x_1+x_2+\cdots+x_n)^{n-2}=\sum_{T\in S}\left(\prod_{i=1}^nx_i^{d_T(v_i)-1}\right), \\ (3)证明恒等式
(x+y)(x+y+z_1+\cdots+z_n)^{n-1}=xy\sum_{I\subseteq\{1,\cdots,n\}}(x+Z_I)^{|I|-1}(y+Z_{I^c})^{|I_c|-1}. \\ 其中I可以为空集, I^C为补集, Z_I=\sum_{i\in I}z_i.
如何评价第二届丘成桐女子中学生数学竞赛笔试试题?
(今天上午参赛同学正在考试,我提前占个位置 各位同学可以提供一下回忆版的试题和解答以供参考 被浏览 34,033你可以邀请下面用户,快速获得回答
没有找到你想邀请的人3 个回答
 Fiddie
Fiddie 数学话题下的优秀答主
数学话题下的优秀答主
好像还没人写解答,那我简单写一下我的解答,如果有误欢迎指出!
1. 求\alpha,\beta使得级数\sum\limits_{n=1}^{\infty}\sum\limits_{m=1}^n\dfrac{1}{n^{\alpha}m^{\beta}}收敛.
解答: 当\alpha\le 1时, 根据
\sum\limits_{m=1}^n\dfrac{1}{n^{\alpha}m^{\beta}} \ge \dfrac{1}{n^{\alpha}}, \\
于是原级数发散. 下设\alpha>1.
(1)当\beta\ge 0时, 由于
\int_{m}^{m+1}\dfrac{1}{x^{\beta}}\mathrm{d}x \le \dfrac{1}{m^{\beta}} \le \int_{m-1}^m\dfrac{1}{x^{\beta}}\mathrm{d}x, \\
所以
\int_1^{n}\dfrac{1}{x^{\beta}}\mathrm{d}x < \sum\limits_{m=1}^n\int_{m}^{m+1}\dfrac{1}{x^{\beta}}\mathrm{d}x \le \sum\limits_{m=1}^n\dfrac{1}{m^{\beta}} \le 1+ \sum\limits_{m=2}^n\int_{m-1}^m\dfrac{1}{x^{\beta}}\mathrm{d}x < 1+ \int_{1}^n\dfrac{1}{x^{\beta}}\mathrm{d}x,\\
(i)当\beta=1时, 上式变成
\ln n < \sum\limits_{m=1}^n\dfrac{1}{m} < 1+\ln n, \qquad \Rightarrow \qquad \dfrac{\ln n}{n^{\alpha}} < \sum\limits_{m=1}^n\dfrac{1}{n^{\alpha}m} < \dfrac{1+\ln n}{n^{\alpha}}.\\
所以当\alpha>1时, 原级数收敛; 当\alpha\le 1时, 原级数发散.
(ii)当\beta\ne 1时, 上式变成
\dfrac{1}{-\beta+1}(n^{-\beta+1}-1) \le \sum\limits_{m=1}^n\dfrac{1}{m^{\beta}} \le 1+\dfrac{1}{-\beta+1}(n^{-\beta+1}-1),\\
此时,
\dfrac{1}{-\beta+1}(n^{-\alpha-\beta+1}-n^{-\alpha}) \le \sum\limits_{m=1}^n\dfrac{1}{n^{\alpha}m^{\beta}} \le \dfrac{1}{n^{\alpha}}+\dfrac{1}{-\beta+1}(n^{-\alpha-\beta+1}-n^{-\alpha}).\\
当\alpha>1且\alpha+\beta-1>1(即\alpha+\beta>2)时, 原级数收敛; 其余情况发散.
(2)当\beta < 0时, 由于
\int_{m-1}^m\dfrac{1}{x^{\beta}}\mathrm{d}x < \dfrac{1}{m^{\beta}} < \int_{m}^{m+1}\dfrac{1}{x^{\beta}}\mathrm{d}x, \\
所以
1+\dfrac{1}{-\beta+1}(n^{-\beta+1}-1) = 1+ \int_{1}^n\dfrac{1}{x^{\beta}}\mathrm{d}x< \sum\limits_{m=1}^n\dfrac{1}{m^{\beta}} < \int_1^{n}\dfrac{1}{x^{\beta}}\mathrm{d}x = \dfrac{1}{-\beta+1}(n^{-\beta+1}-1),\\
此时,
\dfrac{1}{n^{\alpha}}+\dfrac{1}{-\beta+1}(n^{-\alpha-\beta+1}-n^{-\alpha})\le \sum\limits_{m=1}^n\dfrac{1}{n^{\alpha}m^{\beta}} \le \dfrac{1}{-\beta+1}(n^{-\alpha-\beta+1}-n^{-\alpha}) .\\
\alpha>1且\alpha+\beta-1>1(即\alpha+\beta>2)时, 原级数收敛; 其余情况发散.
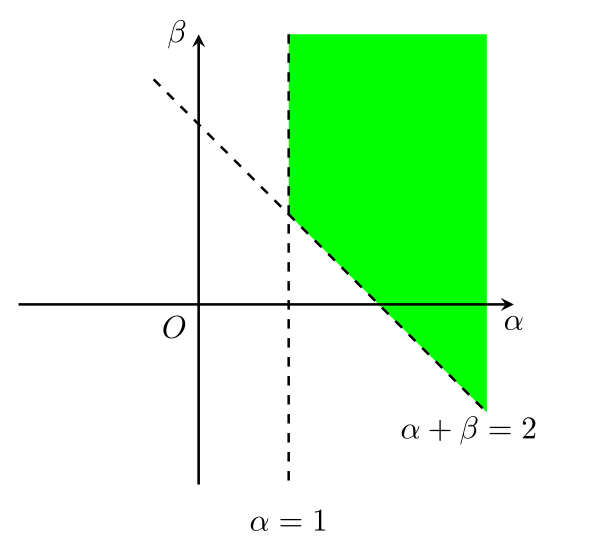 收敛域
收敛域
2. 求椭圆C: \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1的内接六边形面积的最大值.
解答: 设椭圆C上六个点为P_i(\cos\theta_i,\sin\theta_i), i=1,2,3,4,5,6, 并且0<\theta_i<\theta_{i+1}. 内接六边形P_1P_2P_3P_4P_5P_6围成的区域记为\Omega. 为方便起见我们记\theta_7=\theta_1+2\pi, 那么P_7就是P_1.
(i)首先假设\Omega包含原点, 此时\theta_{i+1}-\theta_i < \pi. 于是\Omega的面积为
A(\Omega)=\dfrac{1}{2}\sum\limits_{i=1}^6\sin(\theta_{i+1}-\theta_i). \\
记\alpha_i=\theta_{i+1}-\theta_i, 则\alpha_1+\cdots+\alpha_6=\theta_7-\theta_1=2\pi, 由于\sin x在(0,\pi)上是凹函数, 所以根据Jensen不等式,
\dfrac{1}{6}\sum_{i=1}^6\sin\alpha_i \le \sin\left(\dfrac{1}{6}\sum_{i=1}^6\alpha_i\right)=\sin\dfrac{\pi}{3}=\dfrac{\sqrt{3}}{2}, \\
因此
A(\Omega)=\dfrac{1}{2}\sum_{i=1}^6\sin\alpha_i \le \dfrac{3\sqrt{3}}{2}. \\
等号成立条件是\alpha_1=\cdots=\alpha_6=\dfrac{\pi}{3}, 此时\Omega是边长为1的正六边形.
(ii)若\Omega不包含原点, 则圆C内部有一半与\Omega不相交, 于是A(\Omega) < \dfrac{\pi}{2} < \dfrac{3\sqrt{3}}{2}.
综上, A(\Omega)的最大值为\dfrac{3\sqrt{3}}{2}.
(2)对于一般的情况, 对单位圆x^2+y^2=1沿着两个坐标轴作伸缩变换即可得到椭圆C, 此时面积的最大值也会有相应的伸缩变换, 故A(\Omega)的最大值为\dfrac{3\sqrt{3}ab}{2}.
3. 设G按加法构成群, 满足G=\langle a,b\rangle, 其中a,b为生成元, 且12a+5b=0, 24a+16b=0.
(1)求a的阶的所有可能值.
(2)求群G在同构意义下的群结构.
解: 由条件, G的所有元素形如\{ma+nb|m,n\in\mathbb{Z}\}, 其中a,b\ne 0.
(1)由条件, 24a+10b=2(12a+5b)=0且24a+16b=0, 因此6b=0, 从而b可能是2,3,6阶的.
再由12a+5b=0可得12a-b=0并且72a+30b=0, 所以72a=0. 所以a可能是2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72阶的. 但12a=b\ne 0, 所以a不可能是2,3,4,6,12阶的, 于是只可能是8,9,18,24,36,72阶.
(i)若b是2阶的, 则由24a+16b=0可得24a=0, 所以a只可能是8,24阶的.
①当G=\mathbb{Z}/8\mathbb{Z}, b=4, a=1时, 满足12a+5b=32=0且24a+16b=0.
②当G=\mathbb{Z}/24\mathbb{Z}, b=12, a=1时, 满足12a+5b=72=0且24a+16b=24+192=0.
(ii)若b是3阶的, 则由12a-b=0可得36a-3b=0, 故36a=0, 所以a只可能是9,18,36阶的.
①当G=\mathbb{Z}/9\mathbb{Z}, b=3, a=1时, 满足12a+5b=27=0且24a+16b=72=0.
②当G=\mathbb{Z}/18\mathbb{Z}, b=6, a=5时, 满足12a+5b=90=0且24a+16b=120+96=216=0.
③当G=\mathbb{Z}/36\mathbb{Z}, b=12, a=1时, 满足12a+5b=72=0且24a+16b=24+192=216=0.
(iii)若b是6阶的, 则a只可能是8,9,18,24,36,72阶的.
当G=\mathbb{Z}/72\mathbb{Z}, b=12, a=1时, 满足12a+5b=72=0且24a+16b=24+192=216=0.
综上所述, a的阶的所有可能值是8,9,18,24,36,72.
(2)G中任意元素可以表示为ma+nb=ma+12na=(m+12n)a, 其中m,n\in\mathbb{Z}, 而m+12n可以表示任意整数, 所以G=\langle a\rangle. 由(1), a只可能是8,9,18,24,36,72阶, 所以根据循环群的定义, G在同构意义下只可能是8,9,18,24,36,72阶循环群, 即G只可能与\mathbb{Z}/k\mathbb{Z}(k=8,9,18,24,36,72)同构.
4. 在三维空间V中, 5个两两不同的二维空间两两相交为一维空间, 求交出的一维空间的个数的可能值.
(一定有更方便的做法)
结论1: 若三个二维空间相交得到的一维子空间有两个相同, 则三个一维子空间都相同, 即e_{ij}=e_{ik}能推出e_{ij}=e_{ik}=e_{jk}.
结论1证明: 设三个二维空间为V_i,V_j,V_k. 若e_{ij},e_{jk},e_{ik}有其中两个相同, 例如e_{ij}=e_{ik}, 则(V_i\cap V_j)\cup (V_i\cap V_k)=V_i\cup(V_j\cap V_k)=e_{ij}\supset e_{jk}, 所以必有e_{jk}=e_{ij}. \square
结论2: 若四个二维空间V_i,V_j,V_k,V_l中, V_i与V_j相交的一维子空间等于V_k与V_l相交的一维子空间, 则这四个二维子空间交出来的一维子空间都相同, 即e_{ij}=e_{kl}能推出e_{ij}=e_{jk}=e_{ik}=e_{il}=e_{jl}=e_{kl}.
结论2证明:设四个二维空间为V_i,V_j,V_k,V_l, 由条件, e_{ij}=V_i\cap V_j=V_k\cap V_l=e_{kl}, 但是
\begin{aligned} &\quad (V_j\cap V_k)\cup (V_i\cap V_k)\cup (V_j\cap V_l)\cup (V_i\cap V_l) \\ &=(V_k\cap(V_i\cup V_j)) \cup (V_l\cap(V_i\cup V_j)) \\ &=(V_i\cup V_j)\cap (V_k\cup V_l) = e_{ij}, \end{aligned}\\
所以e_{jk},e_{ik},e_{jl},e_{il}\subset e_{ij}, 从而必有e_{ij}=e_{jk}=e_{ik}=e_{il}=e_{jl}=e_{kl}. \square
证明: 假设二维空间为V_1,V_2,V_3,V_4,V_5, 并且记V_i\cap V_j=e_{ij}是V的一维子空间. 设S为交出的一维空间的个数.
首先, V_1,V_2,V_3之间交出的一维子空间: V_1\cap V_2=e_{12}, V_1\cap V_3=e_{13}, V_2\cap V_3=e_{23}.
(1)若e_{12},e_{13},e_{23}有其中两个相同, 由结论1可知e_{12}=e_{13}=e_{23}. 下面考虑e_{14},e_{24},e_{34}.
①若e_{14},e_{24},e_{34}至少有一个等于e_{12}=e_{13}=e_{23}, 例如e_{14}=e_{12}=e_{13}=e_{23}, 则根据结论1, e_{24}=e_{14}=e_{12}, 并且e_{34}=e_{14}=e_{13}. 于是这六个一维子空间都相同.
(a)若e_{15},e_{25},e_{35},e_{45}至少有一个等于e_{12}=e_{13}=e_{23}=e_{14}=e_{24}=e_{34}, 例如e_{15}等于上述六个一维子空间, 则根据结论1, e_{25}=e_{15}=e_{12}, e_{35}=e_{15}=e_{13}, e_{45}=e_{15}=e_{14}. 所以十个一维子空间都相同, 从而\boxed{S=1}.
(b)若e_{15},e_{25},e_{35},e_{45}都不等于e_{12}=e_{13}=e_{23}=e_{14}=e_{24}=e_{34}, 那么e_{15},e_{25},e_{35},e_{45}也两两不同(不然与结论1矛盾), 从而\boxed{S=5}.
②若e_{14},e_{24},e_{34}都不等于e_{12}=e_{13}=e_{23}, 则e_{14},e_{24},e_{34}两两不同(不然与结论1矛盾),
- (a)若e_{15},e_{25},e_{35}中至少有一个等于e_{12}=e_{13}=e_{23}, 则根据结论1, e_{25}=e_{15}=e_{12}且e_{35}=e_{15}=e_{13}, 即这六个一维子空间相同.
- (a-i)当e_{45}等于e_{12}=e_{13}=e_{23}=e_{15}=e_{25}=e_{35}时, 由结论2, e_{45}=e_{14}=e_{24}=e_{34}, 此时\boxed{S=1}.
- (a-ii)当e_{45}不等于e_{12}=e_{13}=e_{23}=e_{15}=e_{25}=e_{35}时, 也不可能等于e_{14},e_{24},e_{34}之一(不然与结论1矛盾), 此时\boxed{S=5}.
- (b)若e_{15},e_{25},e_{35}中至少有一个等于e_{14}或e_{24}或e_{34}且不等于e_{12}=e_{13}=e_{23}, 根据结论1可知e_{15},e_{25},e_{35}两两不同.
- (b-i)当存在i\in\{1,2,3\}满足e_{i5}=e_{i4}时, 不妨设e_{15}=e_{14}, 则由结论1可知e_{15}=e_{14}=e_{45}. 不可能有两个不同的i,j\in\{1,2,3\}满足e_{i5}=e_{i4}且e_{j5}=e_{j4}, 不然与“e_{15},e_{25},e_{35}两两不同”矛盾. 所以此时不同的一维子空间包括e_{12}=e_{13}=e_{23}, e_{24}, e_{34}, e_{15}=e_{14}=e_{45}, e_{35}, e_{25}, 因此\boxed{S=6}.
- (b-ii)当存在不同的i,j\in\{1,2,3\}满足e_{i5}=e_{j4}时, 不妨设e_{15}=e_{24}, 则根据结论2, e_{15}=e_{24}=e_{12}=e_{14}=e_{25}=e_{45}, 与“e_{14},e_{24},e_{34}两两不同”矛盾.
- (b-iii)当e_{15},e_{25},e_{35}与e_{14},e_{24},e_{34}之间都不相同, 则e_{45}也与这些一维子空间不相同(否则由结论2可推出矛盾), 则\boxed{S=8}.
(2)若e_{12},e_{13},e_{23}两两不同,
①若e_{14},e_{24},e_{34}有两个相同(不可能三个相同, 与结论1矛盾), 不妨设e_{14}=e_{24}=e_{12}(结论1).
- (a)若e_{15},e_{25},e_{35},e_{45}有两个相同(不可能至少三个相同, 与结论1矛盾):
- (a-i)当e_{15}=e_{25}或e_{15}=e_{45}或e_{25}=e_{45}时(只考虑第一种), 根据结论1和结论2有e_{12}=e_{14}=e_{24}=e_{15}=e_{25}=e_{45}, 所以\boxed{S=5}.
- (a-ii)当e_{15}=e_{35}或e_{25}=e_{35}时(只考虑第一种), e_{15}=e_{35}=e_{13}, 所以\boxed{S=6}.
- (a-iii)当e_{35}=e_{45}时, e_{35}=e_{45}=e_{34}, 所以\boxed{S=6}.
- (b)若e_{15},e_{25},e_{35},e_{45}两两不同, 则\boxed{S=8}.
②若e_{14},e_{24},e_{34}也两两不同并且不等于e_{12},e_{13},e_{23}(不然与结论1矛盾).
- (a)若e_{15},e_{25},e_{35},e_{45}有两个相同(不可能至少三个相同, 与结论1矛盾):
- (a-i)当e_{15}=e_{25}或e_{15}=e_{35}或e_{25}=e_{35}时(只考虑第一种), e_{15}=e_{25}=e_{45}, 此时\boxed{S=8}.
- (a-ii)当e_{15}=e_{45}或e_{25}=e_{45}或e_{35}=e_{45}时(只考虑第一种), e_{15}=e_{45}=e_{25}, 此时\boxed{S=8}.
- (b)若e_{15},e_{25},e_{35},e_{45}两两不同, 此时也不会与e_{12},e_{13},e_{23},e_{14},e_{24},e_{34}相同, 此时\boxed{S=10}.
综上, 所有不同的一维子空间个数的可能值为1,5,6,8,10.
5. 在平面直角坐标系中,
(1)三个整点组成的三角形的面积最小值为多少?
(2)圆心在原点、半径为R的圆上一段长为R^{\frac{1}{3}}的圆弧上三点的面积最大为多少?
(3)在(2)中这段圆弧上至多有几个整点?
(1)不妨设其中一个点是原点, 另外两个点为(a_1,b_1)与(a_2,b_2). 则面积为
\dfrac{1}{2}\left|\det\begin{bmatrix}a_1 & b_1 \\ a_2 & b_2\end{bmatrix}\right|=\dfrac{1}{2}|a_2b_1-a_1b_2|. \\
由于a_1,b_1,a_2,b_2都是整数, 所以|a_2b_1-a_1b_2|\ge 1, 等号成立的一个条件是a_1=1,b_1=0,a_2=0,b_2=1, 此时三角形面积为\dfrac{1}{2}. 所以三个整点组成的三角形的面积最小值为\dfrac{1}{2}.
(2)设长为R^{\frac{1}{3}}的圆弧的圆心角为\theta, 则
2\pi R\dfrac{\theta}{2\pi}=R^{\frac{1}{3}}, \\
故\theta=R^{-\frac{2}{3}}.
①当\theta \ge \dfrac{4\pi}{3}即R\le\left(\dfrac{3}{4\pi}\right)^{\frac{3}{2}}时, 面积最大值为\dfrac{3\sqrt{3}}{4}R^2, 此时三个顶点构成等边三角形.
②当\theta < \dfrac{4\pi}{3}即R>\left(\dfrac{3}{4\pi}\right)^{\frac{3}{2}}时, 面积最大值在两个顶点为圆弧端点、一个顶点为圆弧中点取到, 此时面积的最大值为
\begin{aligned} A&=\dfrac{1}{2}R^2\left[\sin\dfrac{\theta}{2}+\sin\dfrac{\theta}{2}-\sin\theta\right] \\ &=\dfrac{1}{2}R^2\left[2\sin\dfrac{R^{-\frac{2}{3}}}{2}-\sin(R^{-\frac{2}{3}})\right]. \end{aligned}\\
(3)由于R>0, 所以根据不等式x-\dfrac{x^3}{6}\le \sin x\le x(x\ge 0), 可知
A \le \dfrac{1}{2}R^2\left[R^{-\frac{2}{3}} - \left(R^{-\frac{2}{3}}-\dfrac{R^{-2}}{6}\right)\right] =\dfrac{1}{12} < \dfrac{1}{2},\\
所以根据(1)可知这段圆弧上不可能有3个整点.
下面构造有2个整点的例子: 考虑圆心为(0,0), 且经过(1,y_0)和(-1,y_0)的圆, 则半径R=\sqrt{1+y_0^2}. 过两点(1,y_0)和(-1,y_0)的圆弧的圆心角为\alpha=2\arctan\dfrac{1}{y_0}, 弧长可以写成y_0的函数:
l(y_0)=\alpha R=2R\arctan\dfrac{1}{y_0}=2\sqrt{1+y_0^2}\arctan\dfrac{1}{y_0}. \\
所以\lim\limits_{y_0\to+\infty}l(y_0)=2. 取y_0充分大使得
l(y_0)=\alpha R<\theta=R^{\frac{1}{3}}, \\
于是此时在弧长为R^{\frac{1}{3}}的圆弧上存在两个整点.
6. n阶矩阵的所有元素均为\pm 1, 求所有此类矩阵的行列式的平均值.
解: 假设A是一个n阶矩阵, 定义\tilde{A}为把A的第一行的1换成-1、-1换成1得到的n阶矩阵, 相当于把A的第一行全都取相反数. 则根据行列式的运算法则, \det(\tilde{A})=-\det A, 即\det(\tilde{A})+\det A=0.
下面固定n阶矩阵的第2\sim n行. 由于第1行有2^n种不同的情况, 所以一共有2^n个不同的矩阵, 把这些矩阵的全体记为\mathscr{A}. 对任意的A\in\mathscr{A}, 都有\tilde{A}\in\mathscr{A}且满足\det(\tilde{A})+\det A=0. 所以\mathscr{A}中所有矩阵的行列式之和为0, 并且跟2\sim n行的元素选取无关.
因此, 此类矩阵的行列式之和都为0, 平均值也为0.
第四题可以对应考虑将二维空间对应为点,所交的一维空间对应为边。题目变为五个顶点两两相连(连且仅连一边),可能边的个数,这里边可能是超边(一个边连多于两个顶点)。然后在K5基础上变化考虑,不变就是10,然后用2维超边代可以是1、2个,每用个2维超边可以减少了2边,然后3维超边可以代1个,对应可以减少5边,最后用4维超边可以代1个,对应减少9边。于是综上可得一维空间可能是1,5,6,8,10个
最后一题貌似是实对称矩阵诶,好像是(n-1)!!*((-1)^(n/2))
标签:15,mathrm,dfrac,beta,2021,2022,alpha,丘成桐,lambda From: https://www.cnblogs.com/Eufisky/p/17451211.html